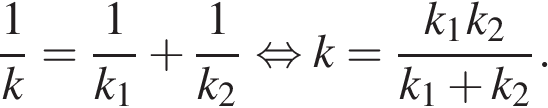Последовательное соединение пружин

Ход работы

II. Актуализация знаний.

• Что такое деформация?
• Сформулировать закон Гука
• Что такое жесткость и в каких единицах она измеряется.
• Дайте понятие об абсолютной и относительной погрешности.
• Причины, приводящие к появлению погрешностей.
• Погрешности, возникающие при измерениях.
• Как чертят графики результатов эксперимента.

Возможные ответы учащихся:

Деформация – изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия; в основе пластических — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.

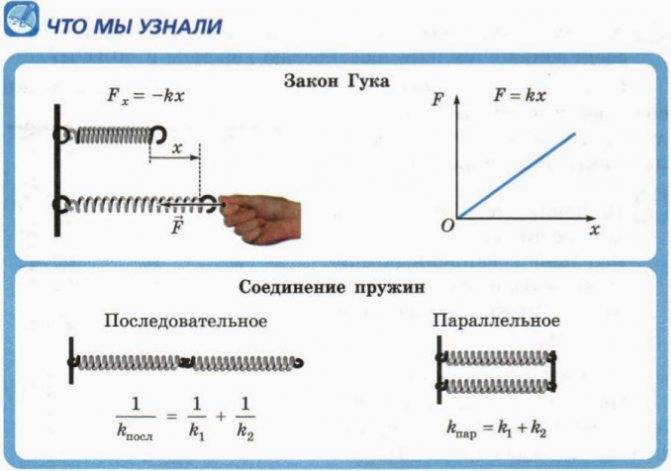
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации». Fупр = –kx

Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Обозначают k. Единица измерения Н/м. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
k = Fупр/x

Измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный и характеризуется погрешностью – отклонением измеренного значения физической величины от ее истинного значения. К причинам, приводящим к появлению погрешностей, относятся: – ограниченная точность изготовления средств измерения. – изменение внешних условий (изменение температуры, колебание напряжения) – действия экспериментатора (запаздывание с включением секундомера, различное положение глаза. ). – приближенный характер законов, используемых для нахождения измеряемых Величин

Погрешности, возникающие при измерениях, делятся на систематические и случайные. Систематические погрешности – это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней. Причины возникновения систематических погрешностей: – несоответствие средств измерения эталону; – неправильная установка измерительных приборов (наклон, неуравновешенность); – несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают; – несоответствие измеряемого объекта с предположением о его свойствах.

Случайные погрешности – это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.

Погрешности средств измерений. Эти погрешности называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки.

При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F_упр = kx

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k_ср.

III. Порядок выполнения работы

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком см. рис.).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины.

По результатам измерений заполните таблицу:

Пружина постоянного усилия:

Пружина постоянной силы устанавливается на барабан, оборачивая его вокруг барабана. Пружина должна быть плотно обернута. Затем свободный конец пружины прилагается к силе нагрузки, например, при использовании противовеса или наоборот.

• Диаметр барабана должен быть больше внутреннего диаметра.
• Диапазон: 10-20% диаметра барабана> Внутренний диаметр.
• На барабане при крайнем растяжении должна быть полуторная пружина.
• Полоса будет нестабильной на больших расширениях, поэтому рекомендуется использовать ее меньшего размера.
• Диаметр шкива должен быть больше исходного диаметра.

Примеры решения задач

ПРИМЕР 1

Задание	Какова работа, совершается при сжатии пружины на величину ? Считать, что сила упругости пропорциональна сжатию, коэффициент упругости пружины равен k.
Решение	В качестве основной формулы используем определение работы вида: Сила по условию пропорциональна величине сжатия, что математически можно представить как: Подставим выражения для силы (1.2) в формулу (1.1):
Ответ

ПРИМЕР 2

Задание	Вагон массой двигался со скоростью . Он ударился о стенку. При ударе каждый буфер вагона сжался на l м. Буферов два. Каковы коэффициенты упругости пружин, если считать, что они равны?
Решение	Сделаем рисунок.

ая энергия пружины?

___

потенциальная энергия пружины?

2. Тело, масса которого 5 кг, находится на высоте 12 м над поверхностью земли. Вычислите его потенциальную энергию:

а) относительно оверхности земли;

б) относительно крыши здания, высота которого 4 м.

___3. Недеформированную пружину динамометра растянули на 10 см, и ее потенциальная энергия стала 0,4 Дж. Каков коэффициент жесткости пружины?

100 Н, а ко второй, жесткостью k2, – 50 Н. Как соотносятся жесткости пружин?

делениями 0 и 1 его шкалы равно 2 см.

k=…………………..

каково значение силы тяжести действующей на груз

G=………………………….

3) для этого задания нужно полное решение нада определить вес астронавта массой 100кг сначала на луне а потом на марсе

4)надо определить обсалютное удлинение пружины жесткостью 50 Н/м если

на неё действуют с силой 1 н и б)к ней подвешено тело массой 20 г

5)астронавт находясь на лун подвесил к пружине деревянный брус массой 1кг. пружина удлинилась на два см. затем астронавт с помощью той же пружины равномерно тянул брус по горизонтальной поверхности. в этом случае пружина удлинилась на 1 см

надо определить

жесткость пружины…………………

величину силы трения…………..

во сколько раз сила трения могла быть больше если бы экспиримент проводился на марсе

плиз нужно через 4 часа я прошу вас

7. В случае уменьшения длины спиральной пружины на 3,5 см возникает сила упругости, равная 1,4 кН. Какой будет сила упругости пружины, если уменьшить ее длину на 2,1 см? 8. При открывании двери длина дверной пружины увеличилась на 0,12 м; сила упругости пружины составляет при этом 4 Н. За которого удлинения пружины сила упругости равна 10 Н? 9. Сила 30 Н растягивает пружину на 5 см. Какая сила растянет пружину на 8 см? 10. В результате растяжения недеформованої пружины длиной 88 мм, до 120 мм возникла сила упругости, равная 120 Н. Определите длину этой пружины в том случае, когда сила, действующая на нее, равна 90 Н. он находится в равновесии.

Формула жесткости пружины – едва ли не самый важный момент в теме об этих упругих элементах. Ведь именно жесткость играет очень важную роль в том, благодаря чему эти комплектующие используются так широко.

Сегодня без пружин не обходится практически ни одна отрасль промышленности, они используются в приборо- и станкостроении, сельском хозяйстве, производстве горно-шахтного и железнодорожного оборудования, энергетике, других отраслях. Они верой и правдой служат в самых ответственных и критических местах различных агрегатов, где требуются присущие им характеристики, в первую очередь жесткость пружины, формула которой в общем виде очень проста и знакома детям еще со школы.

Как можно измерить жесткость

Измерительные приборы

Приборы для испытания пружин на сжатие-растяжение контролируют приложенное усилие с помощью тензометрического датчика, а также изменение их длины, выводя показатели на дисплей. Без специального прибора измерить осевую жесткость можно, используя динамометр и линейку.

Существуют приборы и для измерения поперечной жесткости пружин. Для этого нужно измерить смещение нескольких точек пружины, определив расстояние и угол между ними.

Практическая задача

Самый простой способ измерить жесткость пружины — провести стандартный школьный опыт со штативом и подвешенными на пружине грузиками.

Для измерения осевой жесткости спиральной пружины используют:

• штатив, на котором закрепляют пружину;
• крючок, который крепят на свободный ее конец;
• грузики с известной массой, которые подвешивают на свободный конец пружины;
• линейку, чтобы измерить длину пружины с грузом и без груза.

Проведя несколько измерений с грузиками разной массы и вычислив силу тяжести, воздействовавшую на пружину в каждом из них, можно построить график зависимости длины пружины от приложенного усилия и узнать среднее значение коэффициента жесткости.

Вопрос 8.4 Замена системы пружин эквивалентной пружиной

П

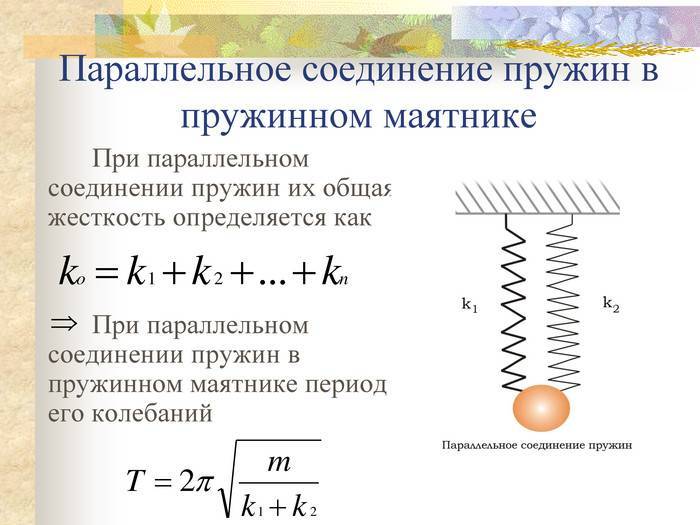
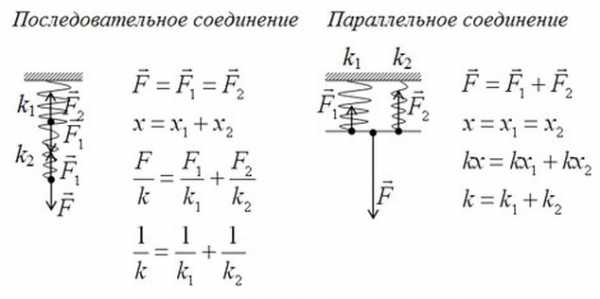
ри описании колебательного движения систему пружин, действующих на материальную точку, заменяют одной пружиной, жесткость которой равна жесткости системы. Эту пружину называют эквивалентной. Рассмотрим три основные схемы соединения пружин.

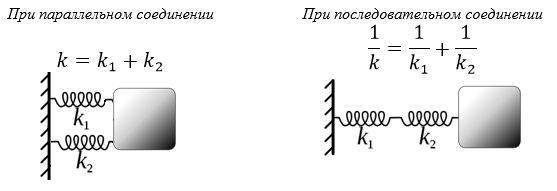
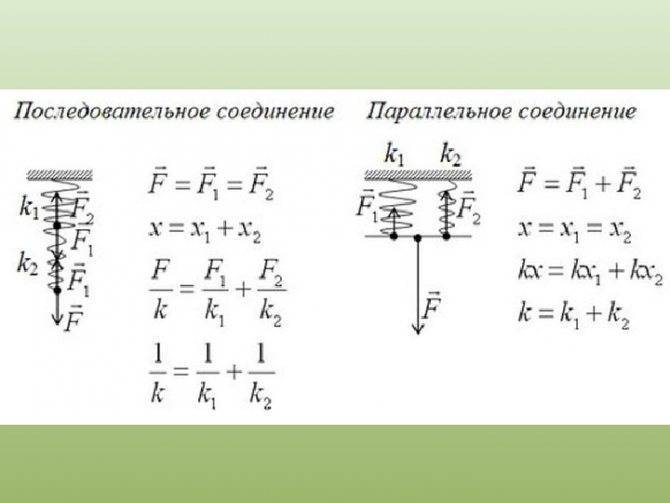
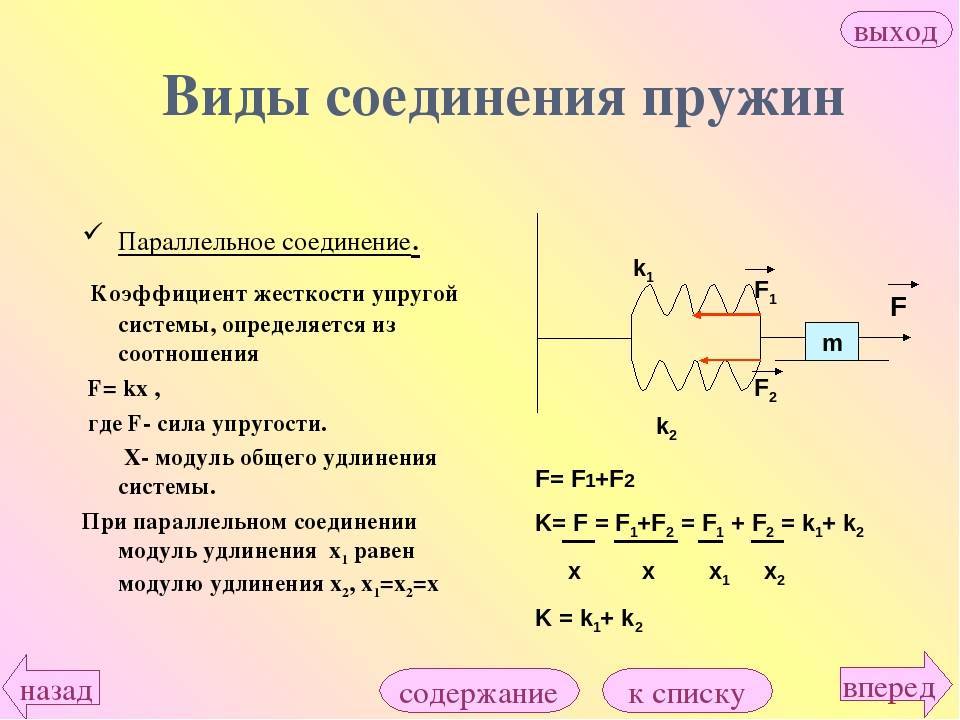
1 Параллельное соединение

(рисунок 8.1).

П

Рисунок 8.1

араллельно соединенные пружины, если их деформации одинаковы, можно заменить эквивалентной пружиной, коэффициент жесткости которой равен сумме коэффициентов жесткости соединенных пружин,

2 Последовательное соединение

(рисунок 8.2).

П

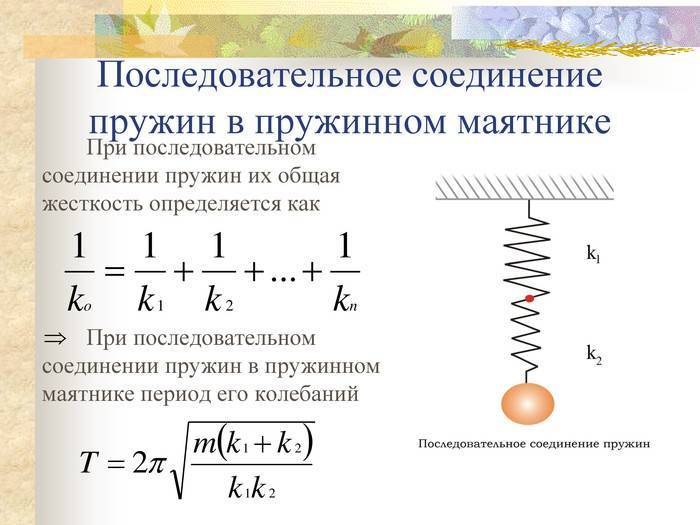
ри последовательном соединении нескольких пружин они могут быть заменены эквивалентной пружиной, податливость которой равна сумме податливостей соединенных пружин (податливостью пружины называют величину, обратную коэффициенту жесткости). Следовательно, коэффициент жесткости эквивалентной пружины в данном случае определяется следующим образом:

3

Рисунок 8.2«Двухстороннее» соединение (рисунок 8.3).

П

ри движении исследуемой материальной точки деформации обоих пружин будут одинаковы. Результирующая сила, действующая со стороны этих пружин на точку, будет равна сумме сил упругости в пружинах 1 и 2. Следовательно, коэффициент жесткости эквивалентной пружины будет равен сумме коэффициентов жесткости пружин 1 и 2:

Любую систему пружин можно представить как набор рассмотренных схем.

Рисунок 8.3

Лекция 9

Динамика материальной системы.

(2 часа, 1 семестр, 2 курс)

Вопрос 9.1Теорема о движении центра масс материальной системы.

Центром масс материальной системы называют точку, радиус-вектор

которой определяется по формуле

,

где

– масса материальной системы;

mi

, – масса и радиус-векторi -й материальной точки.

,

где xi

,yi ,zi – координаты центра массi -го тела системы.

При решении задач динамики материальной системы часто оказывается полезной теорема о движении центра масс

:произведение массы материальной системы

на ускорение ее центра массaCравно геометрической сумме внешних сил, приложенных к системе :

В ходе решения выражение теоремы проецируют на оси координат. При этом получается система уравнений

Использование теоремы о движении центра масс материальной системы для решения задач динамики рекомендуется осуществлять по следующей методике:

1 Изображается материальная система, и указываются все внешние силы, действующие на нее.

2 Выбираются оси координат.

3 Внешние силы, действующие на систему, проецируются на выбранные оси.

4 Записываются выражения координат центра масс системы через координаты центров масс одного из тел системы.

5 Дифференцируя выражения координат центра масс по времени, получают зависимости для скорости и ускорения центра масс системы.

6 Полученные выражения подставляются в систему динамических уравнений.

7 Решается дифференциальное уравнение относительно искомой координаты с учетом заданных начальных условий.

Вопрос 9.2Динамические уравнения движения твердого тела.

Динамические уравнения движения твердого тела устанавливают связь между кинематическими характеристиками движения тела и действующими на него силами.

Поступательное движение тела.

В этом случае динамическое уравнение представляет собой следствие из теоремы о движении центра масс:

,

где m

– масса тела;

– ускорение центра масс тела;

–i -тая сила, действующая на тело.

При решении задач динамическое уравнение поступательного движения тела проецируют на оси координат.

Вращательное движение тела

. Для него динамическое уравнение имеет вид:

,

где Jz

– момент инерции тела относительно оси вращенияz ;

 – угловое ускорение тела;

Miz

– моментi -й силы относительно оси вращения.

При составлении динамического уравнения вращательного движения тела выбирается направление отсчета угла поворота . Моменты сил, вращающих тело против выбранного направления, принимаются отрицательными, а по выбранному направлению – положительными.

Момент инерцииJzявляется мерой инертности тела при вращательном движении. Момент инерции материальной системы относительно данной осиOz определяется как сумма произведений масс всех точек системы на квадраты их расстояний от этой оси:

Для абсолютно твердого тела суммирование по точкам системы заменяется интегрированием по объему

,

где ρ – плотность материала тела;

h

– расстояние от точки с координатамиx ,y ,z до осиOz .

Момент инерции JC

тела относительно осиCz , проходящей через центр массC , называютцентральным моментом инерци и. Если для тела известенрадиус инерцииi , то центральный момент

. Центральные моменты инерции некоторых тел:

1 Тонкий однородный стержень с массой m

и длинойl :

. 2 Тонкое круглое однородное кольцо с массой m

и радиусомR :

. 3 Круглый однородный диск с массой m

и радиусомR :

. studfiles.net

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

Определите по графику коэффициент жесткости тела.

Решение:

Из Закона Гука выразим коэффициент жесткости тела:

F = kx

k = F/x

Снимем значения с графика

Важно выбрать одну точку на графике и записать для нее значения обеих величин

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры:
2 см = 0,02 м
И подставим в формулу:
k = F/x = 2/0,02 = 100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Задачка 2

На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

k = F/x

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

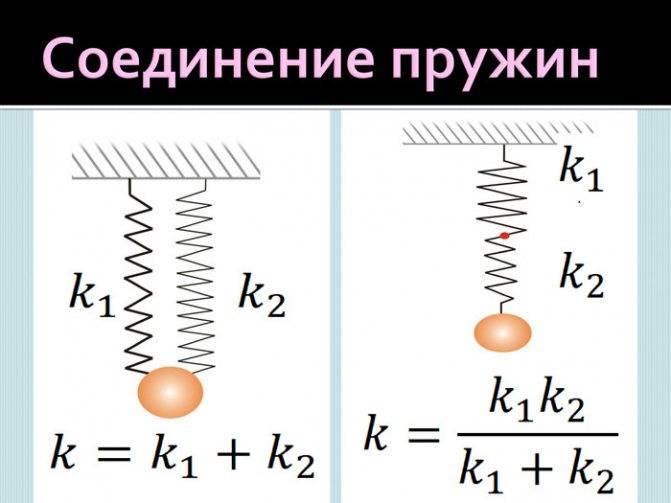
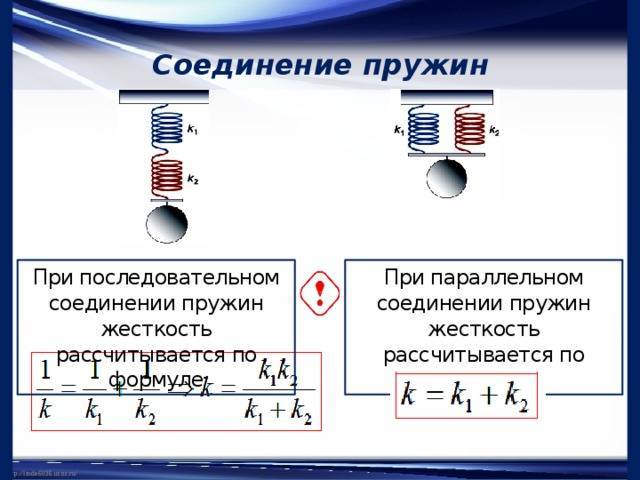
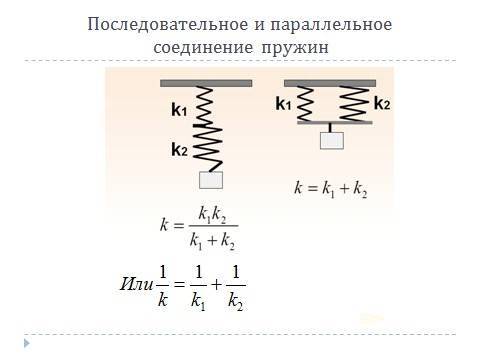
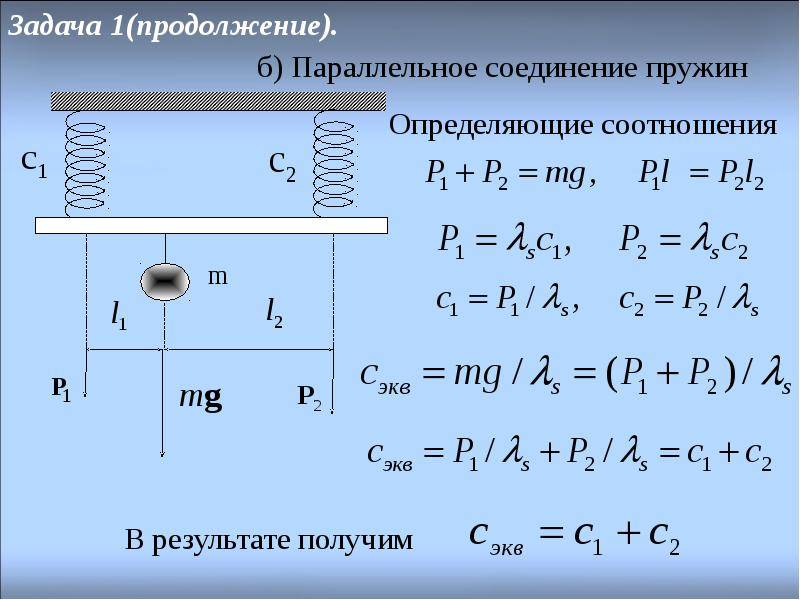
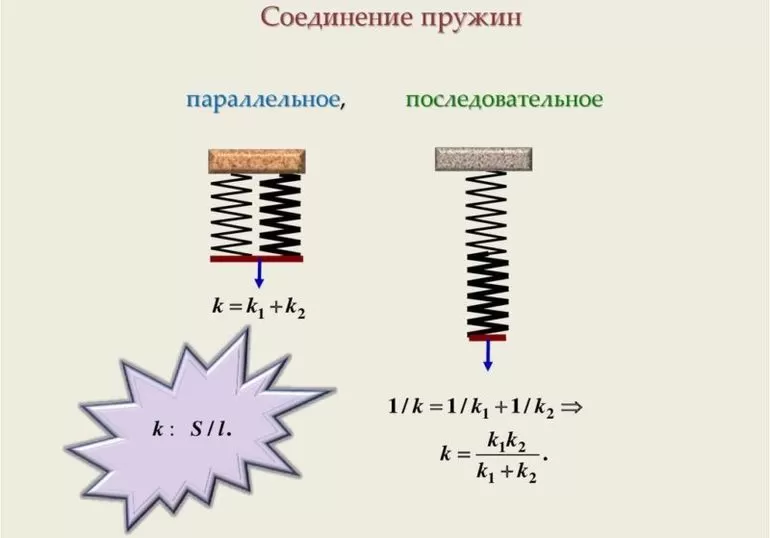
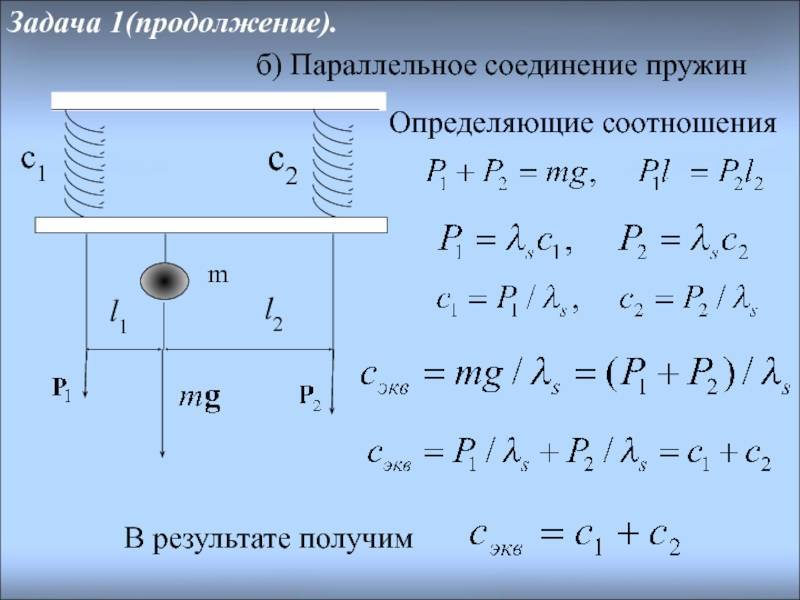
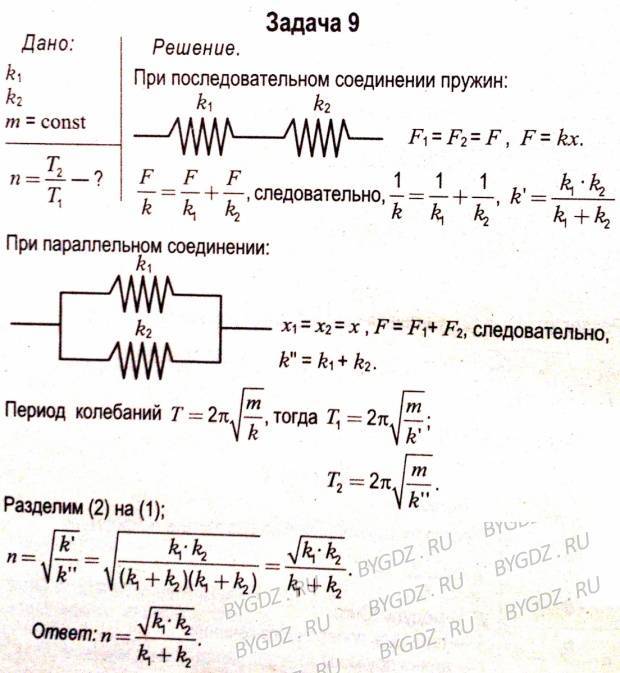
Определение жесткости системы пружин.

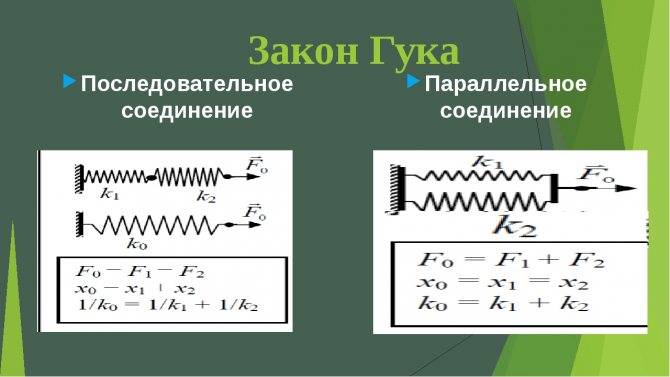
Если пружины соединены параллельно, то деформация всех пружин одинакова и равна λ (рис.2а), нагрузка же, действующая на каждую из пружин, различна: на первую пружину действует сила P1, на вторую P2, и т.д., причем P1+P2+…+Pn=P.

Поэтому

Или т.е. жесткость системы параллельно соединенных пружин Kc равна сумме жесткостей Ki отдельных пружин.

При последовательном соединении пружин (рис.2б) одинаковой для всех пружин является сила нагрузки P, а общая деформация λ складывается из

деформаций λ1, λ2,… ,λn, составляющих пружин.

или

Рис.2.

Отсюда следует, что жесткость системы параллельно соединенных пружин больше жесткостей отдельных пружин, входящих в систему, а жесткость системы последовательно соединенных пружин, наоборот, меньше жесткостей пружин, составляющих эту систему.

Для определения внутренних силовых факторов в витке рассмотрим сечение пружины ( Рис.3).

При растяжении (или сжатии) винтовой цилиндрической пружины в любом поперечном сечении витка возникают крутящий и изгибающий моменты, поперечная и нормальная силы, но при малом угле подъёма винтовой оси проволоки напряжения и перемещения, вызываемые продольной силой и изгибающим моментом малы, и поэтому не учитываются.

Рассечем пружину плоскостью, перпендикулярной ее оси и рассмотрим равновесия отсеченной части пружины,

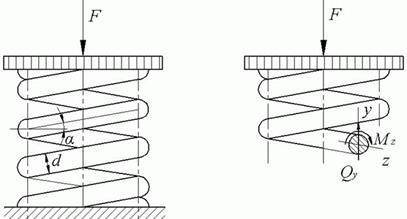
Рис. 3.

Из условия статического равновесия находим, что в поперечных сечениях пружины действуют внутренние силовые факторы в виде поперечного усилия Q=P и крутящего момента MKp=PDcp/2.

От действия усилия Q в поперечном сечении витка пружин возникают касательные напряжения сдвига (рис. 4а), которые равномерно распределены по сечению, площадью А

. От действия крутящего момента MKp возникают касательные напряжения кручения (рис. 4б), суммируя напряжения, получаем эпюру суммарных напряжений (рис. 4в).

Рис.4.

где τ1 — касательные напряжения сдвига

τ2 — касательные напряжения кручения

,

,

где Wp

– полярный момент сопротивления сечения при кручении

Диаметр проволоки значительно меньше двух средних диаметров витка пружины, поэтому можно принять

Изменение продольных размеров (осадку) λ удобно определить энергетическим методом, приравнивая работу А приложенной силы Р и потенциальной энергии деформации U пружины. Работа внешних сил

Потенциальная энергия накапливается, в основном, за счет кручения прутка и поэтому может быть определена

Учитывая, что крутящий Мк=PD/2

и момент инерцииIp=πd4/32 по длине проволоки не изменяются, а длина проволокиl = πdn , получаем

Приравнивая A и U, находим

отсюда

Таким образом, при определении напряжений и перемещений в цилиндрических пружинах учитывают только действие крутящего момента.

Основными материалами пружин являются высокопрочная специальная пру­жинная проволока I, II и III классов диаметром 0,2…5 мм, а также высокоуг­леродистые стали 65, 70, марганцовистая сталь 65Г, кремнистая сталь 60С2А, хромованадиевая сталь 50ХФА и др.

Пружины, предназначенные для рабо­ты в химически активной среде, изготов­ляют из фосфористых БрОФ 6-0,15, БрОФ 4-0,2 и бериллиевой БрБ2 бронз.

3. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ

Внешний вид установки представлен на рис. 5. В состав установки входят:

силовая рама с основанием (6) и (9), элементами горизонтирования (10), кронштейнами (11) и двумя траверсами, выполненных в виде подвиж­ной и неподвижной планок (5);нагрузочные устройства с двумя подвесами (7) и наборами съемных грузов (8);две витые цилиндрические пружины сжатия (1);

два индикатора часового типа (2), указатели (3) и стандартная измери­тельная линейка (4).

Сжимающая сила создается при помощи съемных грузов. Масса одного груза — I кг. Максимальное число грузов на одну пружину — 5. На каждой ступени нагружения фиксируется упругое перемещение (осадка) пружины. Представлены две системы измерений: одна приближенная — измерительная линейка, другая уточненная — индикаторы часового типа.

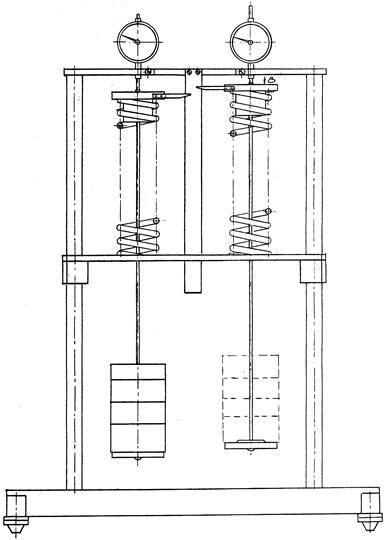
Рис. 5. Лабораторная установка МЗ

Ход работы

II. Актуализация знаний.

• Что такое деформация?
• Сформулировать закон Гука
• Что такое жесткость и в каких единицах она измеряется.
• Дайте понятие об абсолютной и относительной погрешности.
• Причины, приводящие к появлению погрешностей.
• Погрешности, возникающие при измерениях.
• Как чертят графики результатов эксперимента.

Возможные ответы учащихся:

Деформация – изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия; в основе пластических — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.

Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации». Fупр = –kx

Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Обозначают k. Единица измерения Н/м. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как: k = Fупр/x

Измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный и характеризуется погрешностью – отклонением измеренного значения физической величины от ее истинного значения. К причинам, приводящим к появлению погрешностей, относятся: – ограниченная точность изготовления средств измерения. – изменение внешних условий (изменение температуры, колебание напряжения) – действия экспериментатора (запаздывание с включением секундомера, различное положение глаза. ). – приближенный характер законов, используемых для нахождения измеряемых Величин

Погрешности, возникающие при измерениях, делятся на систематические и случайные. Систематические погрешности – это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней. Причины возникновения систематических погрешностей: – несоответствие средств измерения эталону; – неправильная установка измерительных приборов (наклон, неуравновешенность); – несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают; – несоответствие измеряемого объекта с предположением о его свойствах.

Случайные погрешности – это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.

Погрешности средств измерений. Эти погрешности называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки.

При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F_упр = kx

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k_ср.

III. Порядок выполнения работы

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком см. рис.).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины.

По результатам измерений заполните таблицу:

Типы пружин

Пружины можно классифицировать по направлению прилагаемой нагрузки:

• пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны «виток к витку»; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
• пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.

Готовые работы на аналогичную тему

• Курсовая работа Жесткость пружины, формула 440 руб.
• Реферат Жесткость пружины, формула 250 руб.
• Контрольная работа Жесткость пружины, формула 250 руб.

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип — запасать энергию упругой деформации и возвращать ее.

Заключение.

Значение модуля сдвига (G

) материала проволоки в существенной мере влияющее на жесткость пружины (C

)
в реальности колеблется от номинально принятого до ±10%. Это обстоятельство и определяет в первую очередь наряду с геометрической точностью изготовления пружины «правильность» расчетов усилий и соответствующих им перемещений.

Почему в расчетах не используются механические характеристики (допускаемые напряжения) материала проволоки кроме модуля упругости? Дело в том, что, задаваясь углом подъема витка и индексом пружины в ограниченных диапазонах значений, и придерживаясь правила: «угол подъема в градусах близок значению индекса пружины», мы фактически исключаем возможность возникновения касательных напряжений при эксплуатации превышающих критические величины. Поэтому проверочный расчет пружин на прочность имеет смысл производить лишь при разработке пружин для серийного производства в особо ответственных узлах. Но при таких условиях кроме расчетов всегда неизбежны серьезные испытания…

Прошу
УВАЖАЮЩИХ
труд автора скачать файл
ПОСЛЕ ПОДПИСКИ
на анонсы статей.

ОСТАЛЬНЫМ можно скачать просто так… – никаких паролей нет!

Определение

Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости
.

Чаще всего ее обозначают ${\overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.

Рассмотрим пружину, на которую действует растягивающая сила ($\overline{F}$), которая направлена вертикально вниз (рис.1).

Силу $\overline{F\ }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${\overline{F}}_u$), уравновешивающая силу $\overline{F\ }$. Если деформация является небольшой и упругой, то удлинение пружины ($\Delta l$) прямо пропорционально деформирующей силе:

\

где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.

Жесткость (как свойство) – это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости – это основная характеристика жесткости (как свойства тела).

Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:

где $G$ – модуль сдвига (величина, зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.

Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:

\=\frac{\left}{\left}=\frac{Н}{м}.\]

Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.