Деформация изгиба

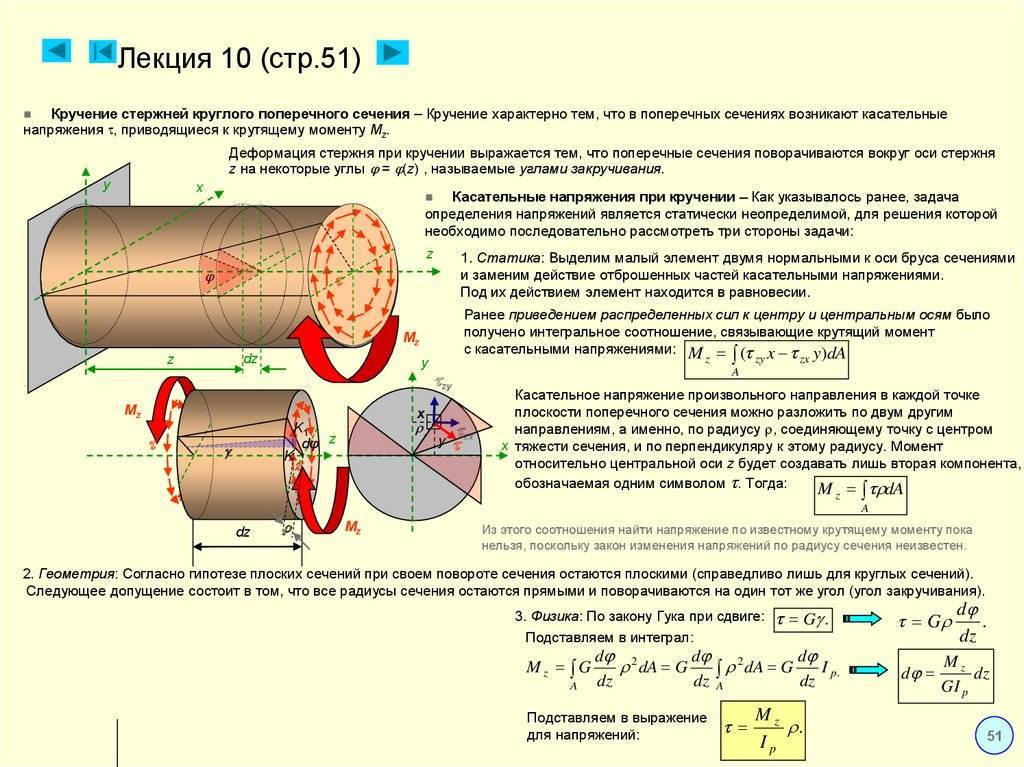
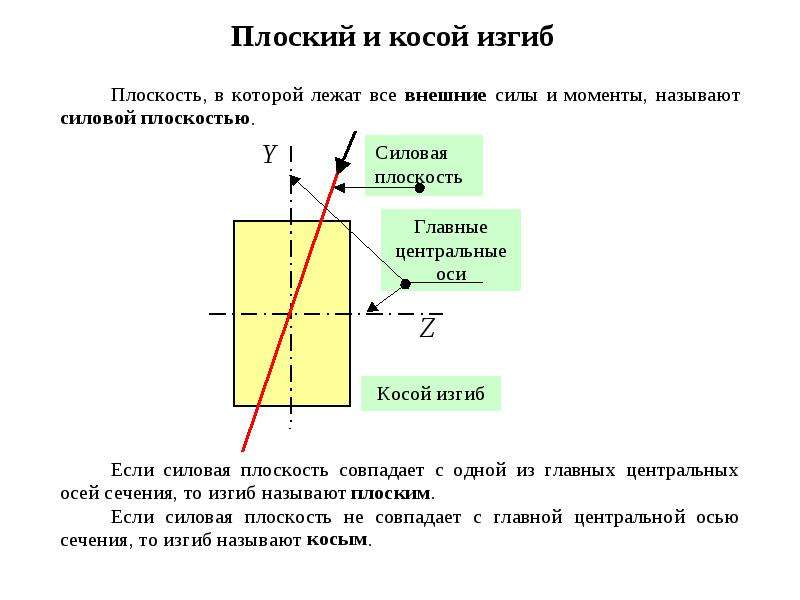
Порядок выполнения и обработка результатов

Определение величины прогибов и углов поворота спорных сечений производится в следующей последовательности.

Установка заранее подготавливается лаборантом (рис. 9.2,б) для выполнения на ней опыта по заданной схеме погружения балки (рис. 9.2.а).

Для заданной расчетной схемы в сечениях установки индикаторов производим подсчет перемещении любым из известных методов (т.е. находим два вертикальных перемещения у_1Т и у_2Т и два угловых перемещения в опорах θ_СТ, θ_KТ). Расчеты линейных и угловых перемещений могут быть выполнены на ЭВМ.

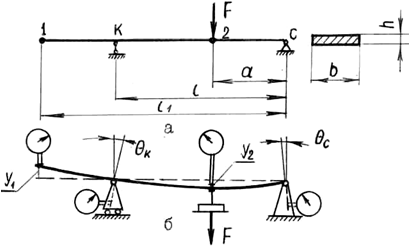
Рис. 9.2. Схема к определению перемещений

Затем приступаем к опытному определению этих же перемещений, для чего снимаем начальные показания со всех индикаторов и данные записываем в журнал.

Устанавливаем на гиревой подвес гирю весом, соответствующим заданной нагрузке F (например, 10 Н), и снимаем новые показания со всех индикаторов, записав их в журнал и подсчитав приращения.

Последовательно догружаем балку 2-3 раза дополнительными гирями того же веса, при этом общая нагрузка на гиревой подвес не должна превышать 60 Н.

После каждого нагружения записываем в журнал наблюдений показания индикаторов и подсчитываем приращения.

По окончании опыта балку разгружаем и сравниваем показания индикаторов с первоначальным.

Для подсчета опытных значений вертикальных перемещений в сечениях 1 и 2 балки подсчитываем средние арифметические приращения по каждому индикатору, замеряющему вертикальные перемещения — ΔП_СР, которые и будут соответственно у_1ОП = ΔП_1СР и у_2ОП = ΔП_2СР в единицах измерения шкалы индикаторов.

Величина углов поворота определяется по формуле

θ_i = ΔП_iСР/ l_С ,

где ΔП_iСР – средние арифметические приращения отсчетов индикаторов, измеряющих длину дуги поворотов опорных сечений; l_С = 150 мм – расчетная длина рычага (радиус дуги).

Сравнение опытных результатов с теоретическими производим по формулам

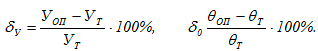
Полученные данные заносятся в журнал и делаются соответствующие выводы.

Измерение деформации

При проектировании и эксплуатации различных механизмов, технических объектов, зданий, мостов и других инженерных сооружений очень важно знать величину деформации материалов. Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью

Для этого используют приборы, называемые тензометрами

Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами.

Тензометр состоит из тензометрического датчика и индикаторов. В него также может быть включено регистрирующее устройство.

В зависимости от принципа действия тензометры бывают оптические, пневматические, акустические, электрические и рентгеновские.

В основу оптических тензометров положено измерение деформации нити из оптоволокна, приклеенной к объекту исследования. Пневматические тензометры фиксируют изменение давления при деформации. В акустических тензометрах с помощью пьезоэлектрических датчиков проводятся измерения величин, на которые изменяются скорость звука и акустическое затухание при деформации. Электрические тензометры вычисляют деформацию на основе изменений электрического сопротивления. Рентгеновские определяют изменение межатомных расстояний в кристаллической решётке исследуемых металлов.

Вплоть до 80-х годов ХХ века сигналы датчиков регистрировались самописцами на обыкновенной бумажной ленте. Но когда появились компьютеры и начали бурно развиваться современные технологии, стало возможным наблюдать деформации на экранах мониторов и даже подавать управляющие сигналы, позволяющие изменить режим работы тестируемых объектов.

Методы расчета перемещений

Существует несколько способов расчета линейных y и угловых θ перемещений при изгибе:

Метод начальных параметров (МНП)

Перемещения рассчитываются по уравнениям МНП

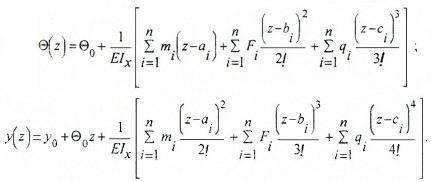
Считается относительно простым методом расчета перемещений в прямых балках с постоянной жесткостью сечения. Данный способ не применим для расчета прогибов и углов наклона в балках переменного сечения, с изогнутой или ломаной осью и в рамах.Подробнее >>

Интеграл Мора

Интеграл Мора относится к энергетическим методам расчета перемещений. В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем. Подробнее >>

Способ Верещагина

Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем. Подробнее >>

Метод интегрирования дифференциального уравнения упругой линии балки

Непосредственное интегрирование дифференциального уравнения упругой линии является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.

По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.

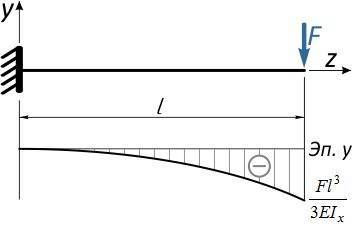
Эти вычисления и построения необходимы для проверки балок на жесткость.

Примеры решения задач >Лекции по сопромату >

Пластическая и упругая деформация

В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина

Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму

Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.

За счет наличия деформационных способностей все известные материалы обладают набором полезных свойств – пластичностью, хрупкостью, упругостью, прочностью и другими. Исследование этих свойств достаточно важная задача, позволяющая выбрать или изготовить необходимый материал. Кроме того, само по себе наличие деформации и его детектирование часто бывает необходимо для задач приборостроения, для этого применяются специальные датчики называемые экстензометрами или по другому тензометрами.

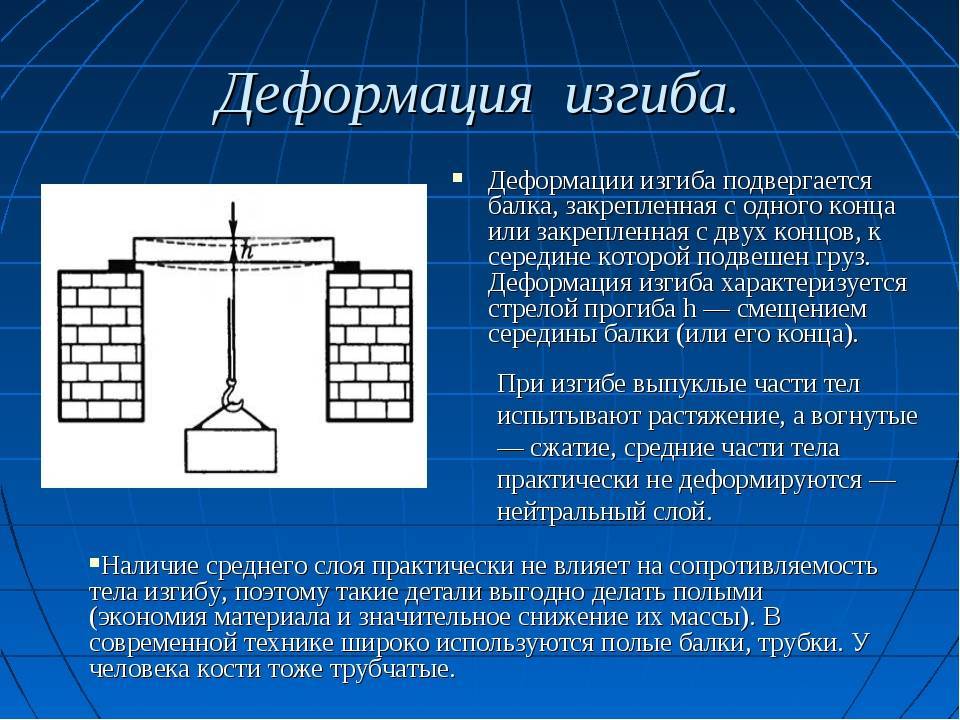
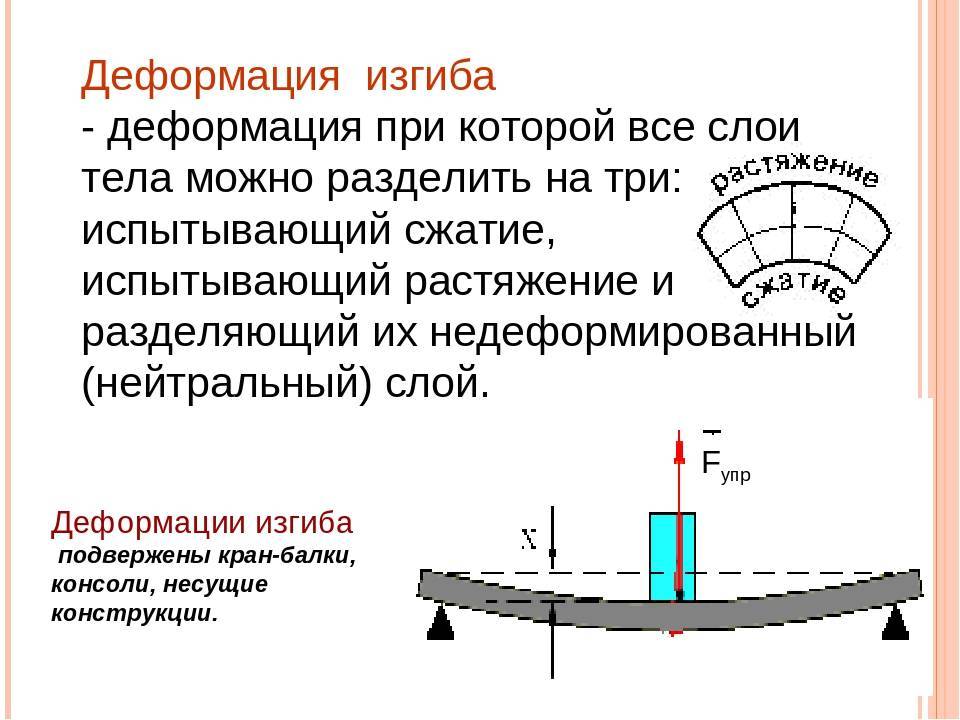
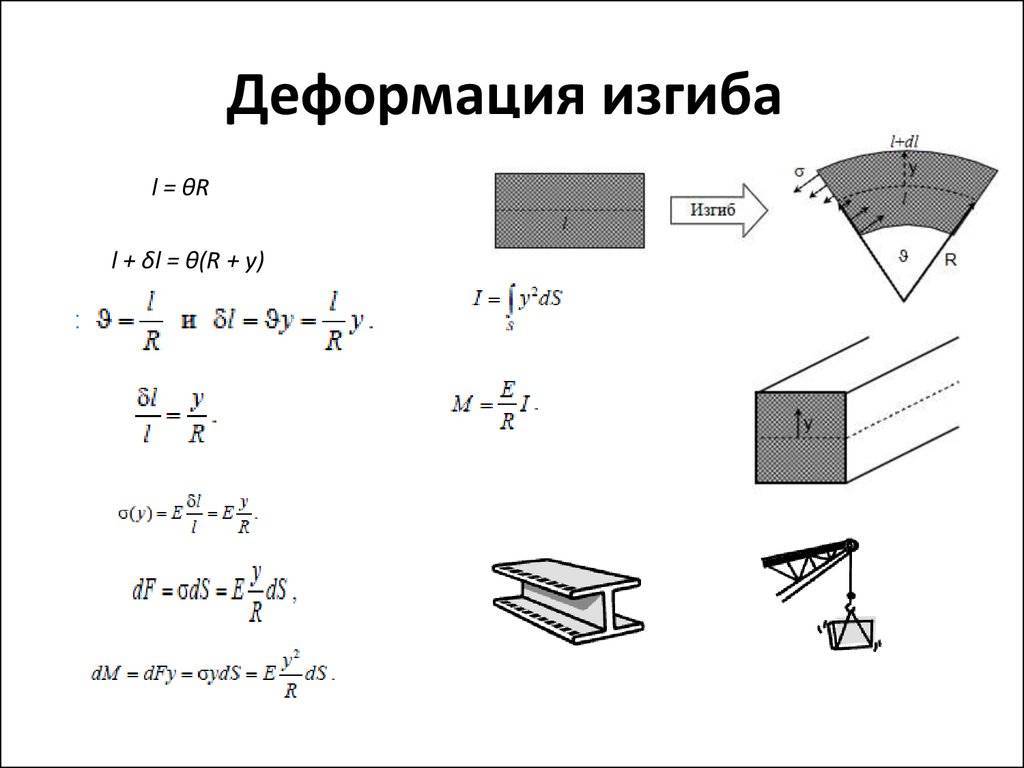
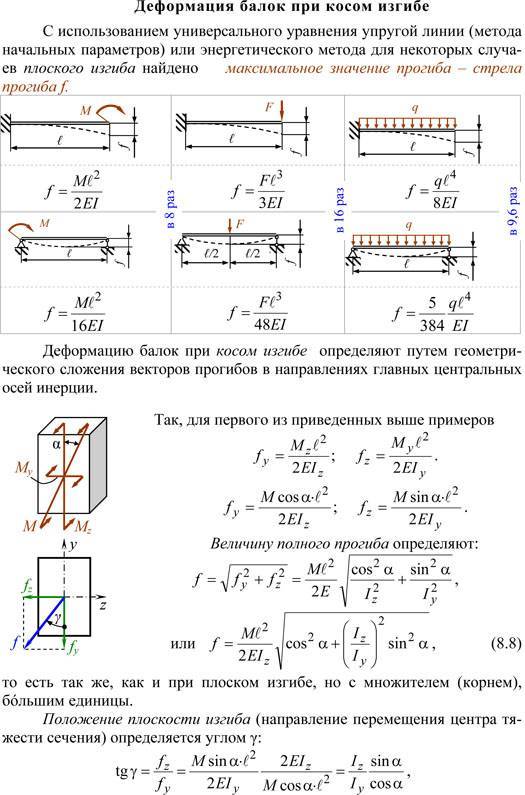
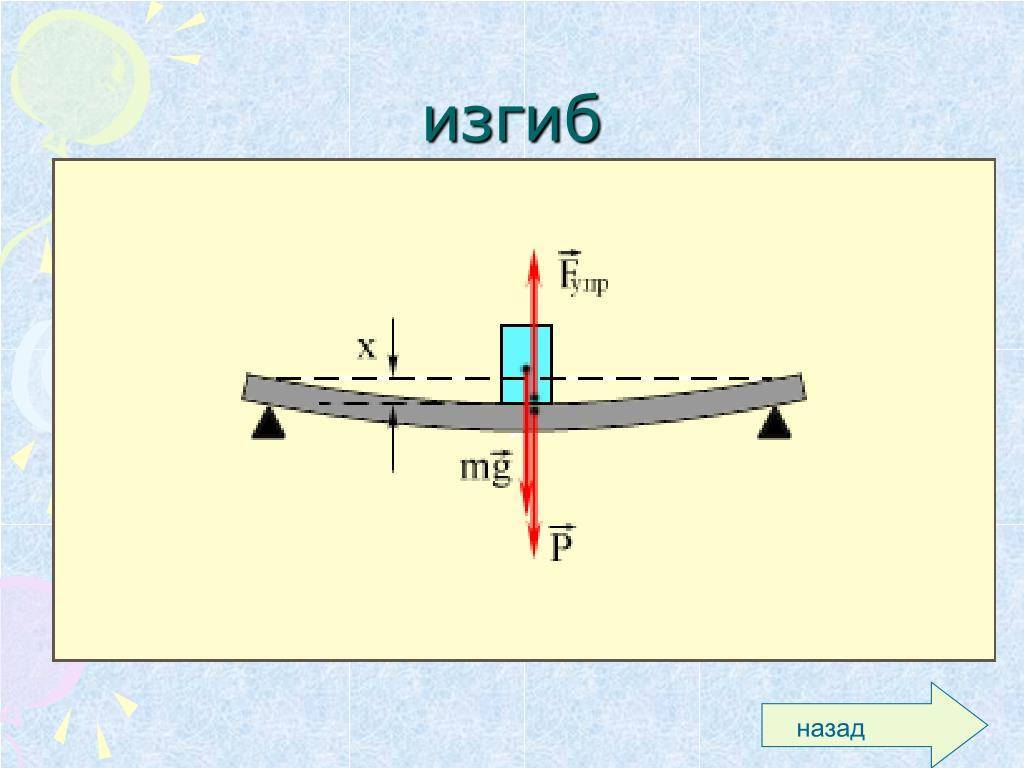
ИЗГИБ

ИЗГИБ

– один из основных видов деформации балки, когда прямолинейная балка под действием внешних нагрузок приобретает криволинейную форму. (Корни слова «балка» – немецкие и первоначально это слово означало «бревно»). Во многих конструкциях балка является основным элементом; примером являются многие типы перекрытий, мостов и т.д. Также по теме: МЕХАНИКА

Балка как конструктивный элемент обычно или закреплена концами на соответствующих опорах, или одним концом заделана в стену, тогда как другой конец оказывается свободным (в этом случае балку называют «консоль»), рис.1 (а, б).

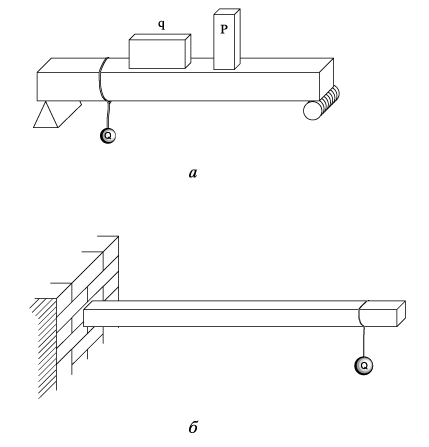
В некоторых местах балка взаимодействуют с другими телами; схематизируя ситуацию (рис. 2), говорят, что в известных точках к балке приложены заданные сосредоточенные силы P

,Q или распределенные нагрузки интенсивностиq (килоньютонов на метр).

Примером распределенных нагрузок является собственный вес балки или вес достаточно длинного постороннего тела, лежащего на балке (например, снега). Нагрузки (или их часть), направленные перпендикулярно к балке, вызывают ее изгиб; направленные вдоль балки вызывают растяжение или сжатие. Задачей теории изгиба балок является определение прогиба балки под нагрузками, а также напряжений и деформаций в материале балки, естественно, что форма, размеры, материал балки и внешние нагрузки считаются заданными. Затем, при расчете на прочность, задачу трансформируют так: каковы должны быть размеры сечения балки, чтобы при заданных нагрузках напряжения не превышали бы допустимых значений?

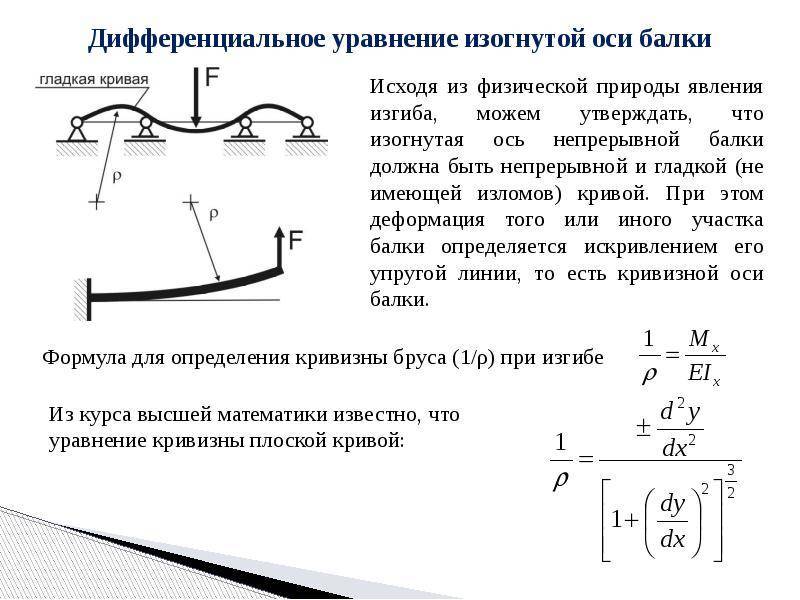
Теория изгиба балки была создана Я.Бернулли и Л.Эйлером на рубеже 17–18 вв. Для простоты балка заменяется отрезком прямой, причем считается, что упругие свойства этого отрезка такие же, как у исходной балки. После приложения нагрузок отрезок изгибается и становится криволинейным. Получившаяся кривая называется упругой линией или эластикой. Задача – найти ее уравнение у

=f (x ). Решение этой задачи основано на утверждении, что в каждой точке упругой линии ее кривизна пропорциональна изгибающему моменту внешних сил, который зависит от координатыx и обозначаетсяM (x ). Так как при малых прогибах, которые в первую очередь интересуют инженеров, кривизна кривой практически равна ее второй производной, можно записать дифференциальное уравнение:

Коэффициент пропорциональности EJ

называется изгибной жесткостью, он определяет способность балки сопротивляться изгибу и равен произведению модуля упругости материала балкиE на момент инерции сечения балкиJ , который для прямоугольного бруса выражается формулой

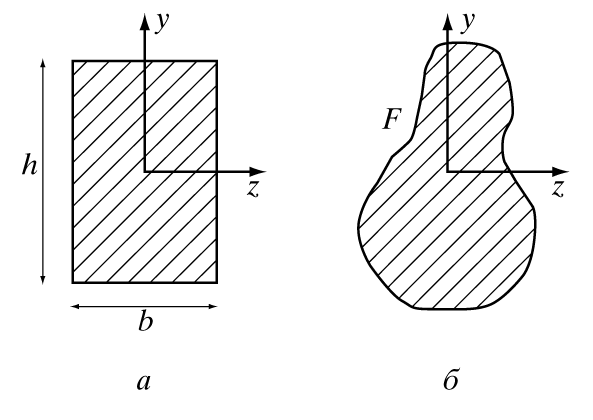
где b

– ширина сечения, аh – высота (рис. 3,а).

Если сечение балки есть фигура F

(рис. 3,б), и начало координат проходит через центр масс сечения, то

J

= тт y\up122dF т.е. момент инерции площади F

определяется как двойной интеграл по этой площади. Название «момент инерции» связано с тем, что этот интеграл в динамике твердого тела связан с инерционными характеристиками тела.

Изгибная жесткость учитывает и упругость материала, и форму и размеры сечения балки.

Изгибающий момент M

(x ) полностью определяется величиной и положением нагрузок и находится по правилам статики. Например, если в консольной балке, нагружаемой на конце силойP , (рис. 2), мысленно провести сечение через точку с координатойx , то момент силыP относительно точкиx выражается очевидной формулой

M = Px

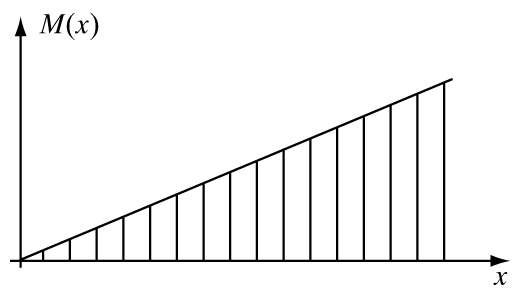
(система координат показана на рис. 4), при изменении расстояния сечения от конца балки момент M

растет линейно; этот график называют эпюрой изгибающего моментаM (x ). Напряжения s в сечениях балки пропорциональныM (x ):

(координата y

отсчитывается вверх от центра сечения).

В качестве примера можно рассмотреть две одинаковые балки: одну – на двух шарнирных опорах, другую – консольную, нагруженные одинаковыми силами P

в середине пролета и на конце соответственно. Длина балокl , сечение – прямоугольникb ×h . Прогиб первой балки в середине пролета равен

Прогиб на конце второй балки равен

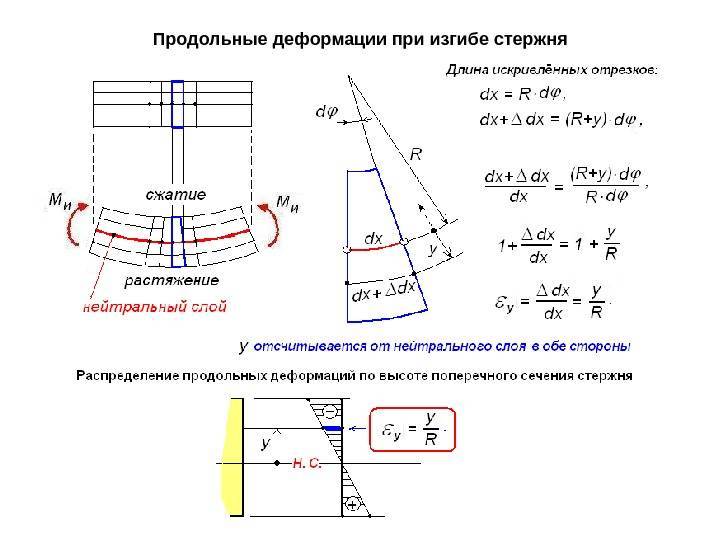
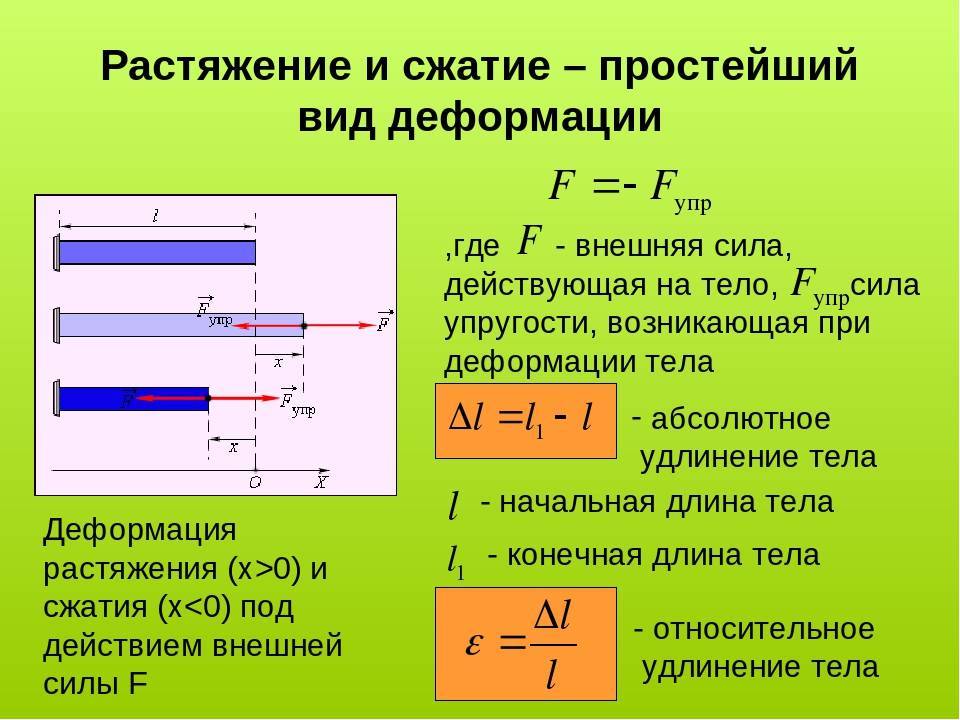
Для сравнения укажем, что если ту же балку растягивать силой P

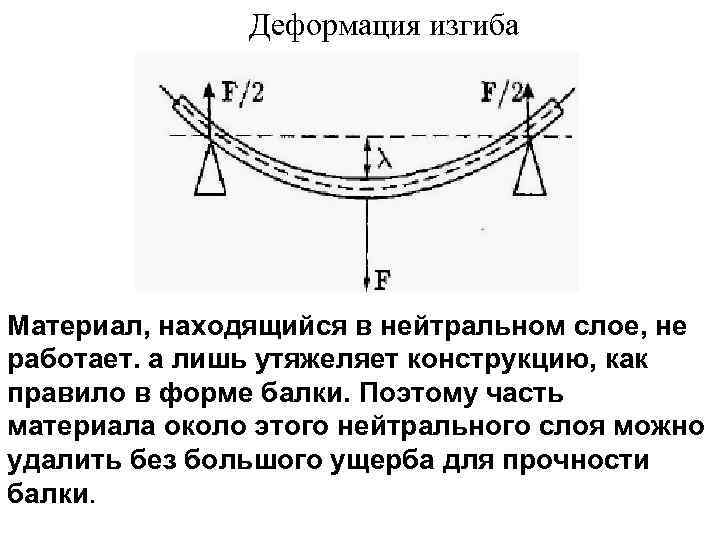
, то ее удлинение будет равно . Напряжения и деформации в изогнутой балке распределены таким образом, что внешние волокна растянуты, а внутренние – сжаты, причем и напряжения s, и деформации e растут пропорционально расстоянию от середины сечения балки, точнее – от нейтральной линии, где s = 0, и e = 0. Другими словами, внешние слои балки несут большую часть нагрузки, внутренние – значительно меньшую. Поэтому целесообразно так организовать форму сечения балки, чтобы большая часть материала была удалена от центра сечения. Двутавровые (т.е. в виде двойного «Т») и трубчатые сечения балок являются типичными примерами оптимальных (т.е. наилучших в некотором смысле) сечений.

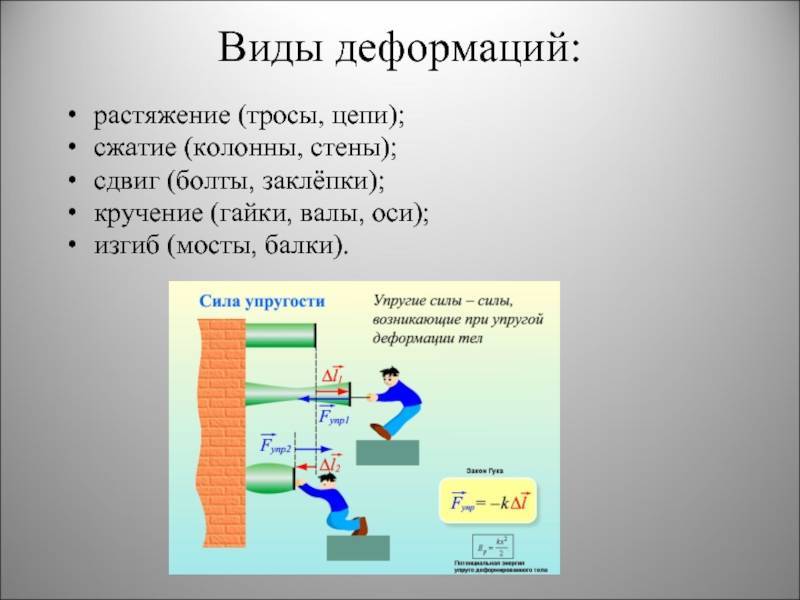
Примеры деформации разных видов

1. Играем на гитаре — кратковременно растягиваем струны

2. Садимся в автомобиль — пружины подвески сжимаются

3. Сидим на тонкой доске — доска прогибается

4. Затягиваем шуруп — происходит кручение отвёртки (хоть мы и не видим деформацию отвёртки)

5. Двигаем расшатанный стул — происходит сдвиг сиденья относительно пола

{"questions":,"explanations":,"answer":}},"hints":},{"content":"Какому виду деформации подвергается мяч при ударе?`choice-7`","widgets":{"choice-7":{"type":"choice","options":,"explanations":,"answer":}},"hints":},{"content":"Упругую дощечку сломали пополам. Какой вид деформации произошёл?`choice-16`","widgets":{"choice-16":{"type":"choice","options":,"explanations":,"answer":}},"hints":}]}

Перемещения при изгибе.

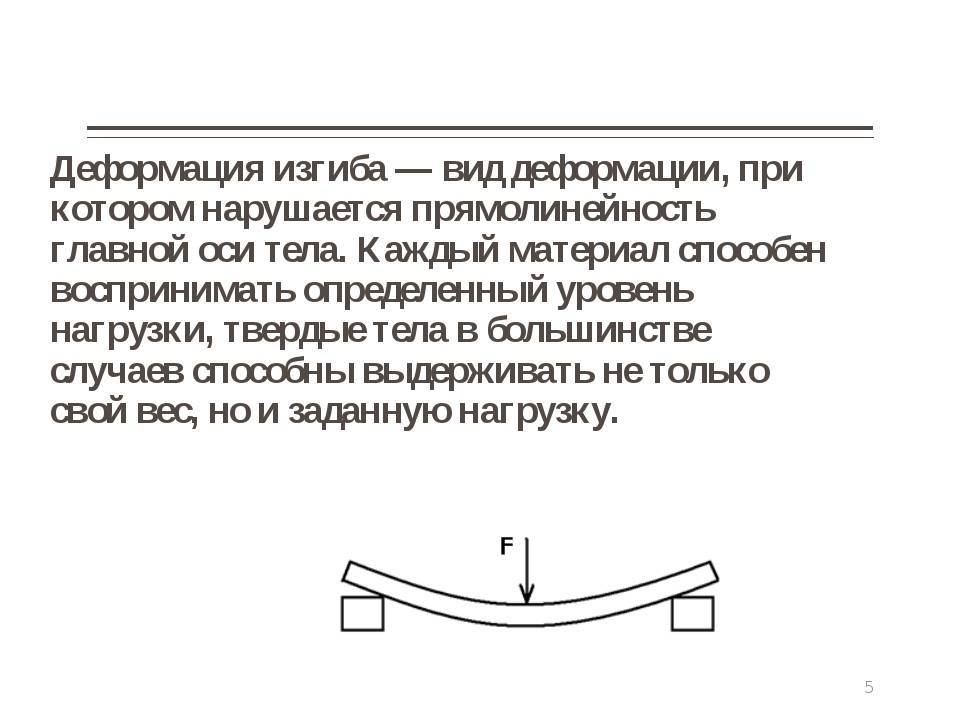
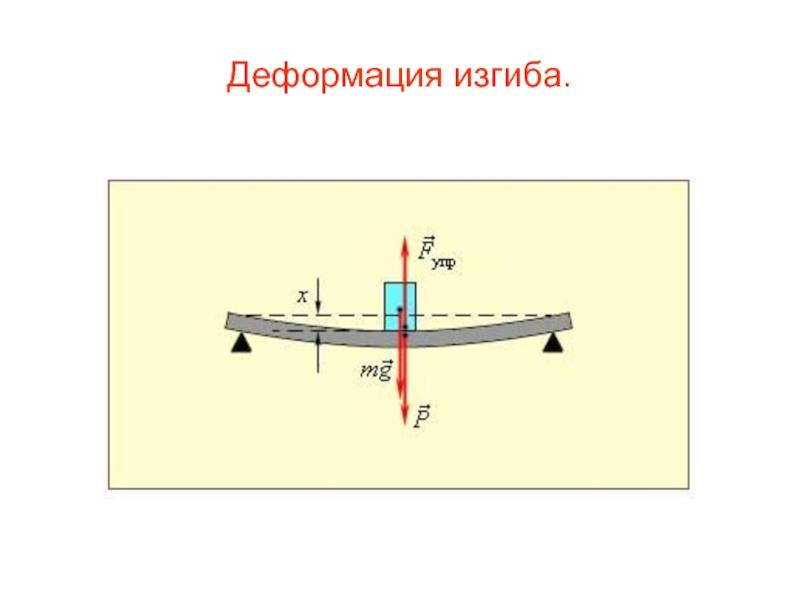
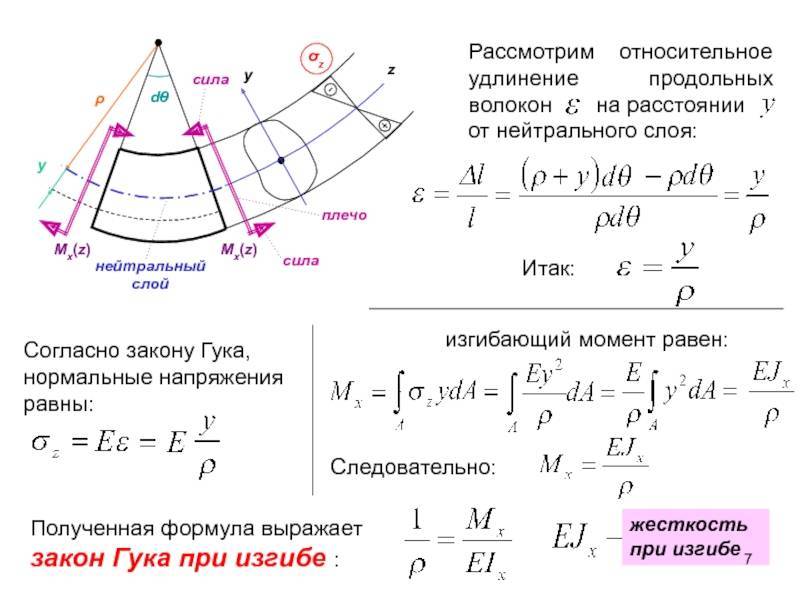
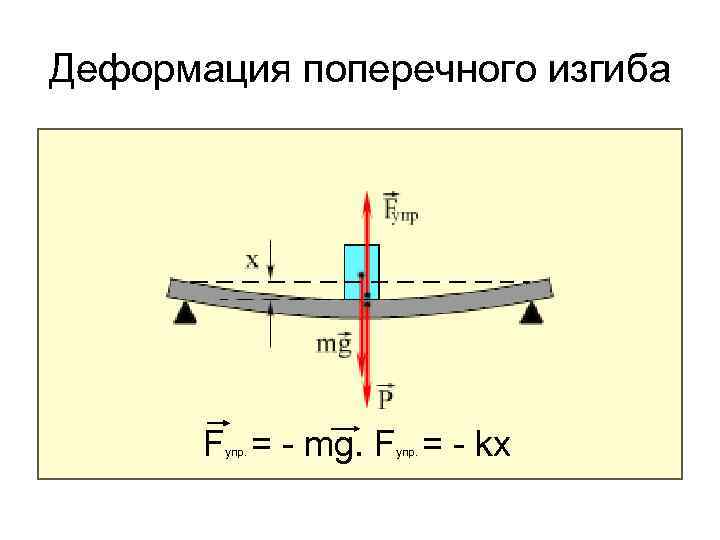
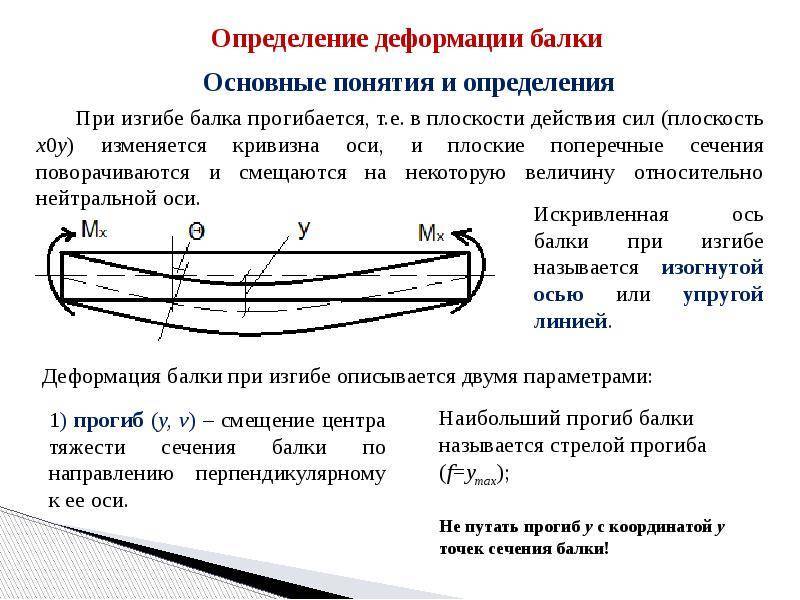
Под действием нагрузки при изгибе ось балки искривляется. При этом наблюдается растяжение волокон на выпуклой и сжатие – на вогнутой частях балки. Кроме того, происходит вертикальное перемещение центров тяжести поперечных сечений и их поворот относительно нейтральной оси. Для характеристики деформации при изгибе используют следующие понятия:

Прогиб балки Y – перемещение центра тяжести поперечного сечения балки в направлении, перпендикулярном к ее оси.

Прогиб считают положительным, если перемещение центра тяжести происходит вверх. Величина прогиба меняется по длине балки, т.е. y = y (z)

Угол поворота сечения – угол θ, на который каждое сечение поворачивается по отношению к своему первоначальному положению. Угол поворота считают положительным при повороте сечения против хода часовой стрелки. Величина угла поворота меняется по длине балки, являясь функцией θ = θ (z).

Самыми распространёнными способами определения перемещений является метод Мора и правило Верещагина.

Дифференциальные зависимости Журавского.

Между интенсивностью q распределенной нагрузки, выражениями для поперечной силы Q и изгибающего момента М установлены дифференциальные зависимости:

На основе этих зависимостей можно выделить следующие общие закономерности эпюр поперечных сил Q и изгибающих моментов М:

Особенности эпюр внутренних силовых факторов при изгибе.

1.

На участке балки, где нет распределенной нагрузки, эпюра Q представленапрямой линией , параллельной базе эпюре, а эпюра М — наклонной прямой (рис. а).

2.

В сечении, где приложена сосредоточенная сила, на эпюре Q должен бытьскачок , равный значению этой силы, а на эпюре М —точка перелома (рис. а).

3.

В сечении, где приложен сосредоточенный момент, значение Q не изменяется, а эпюра М имеетскачок , равный значению этого момента, (рис. 26, б).

4.

На участке балки с распределенной нагрузкой интенсивности q эпюра Q изменяется по линейному закону, а эпюра М — по параболическому, причемвыпуклость параболы направлена навстречу направлению распределенной нагрузки (рис. в, г).

5.

Если в пределах характерного участка эпюра Q пересекает базу эпюры, то в сечении, где Q = 0, изгибающий момент имеет экстремальное значение Mmax или Mmin (рис. г).

Что это такое?

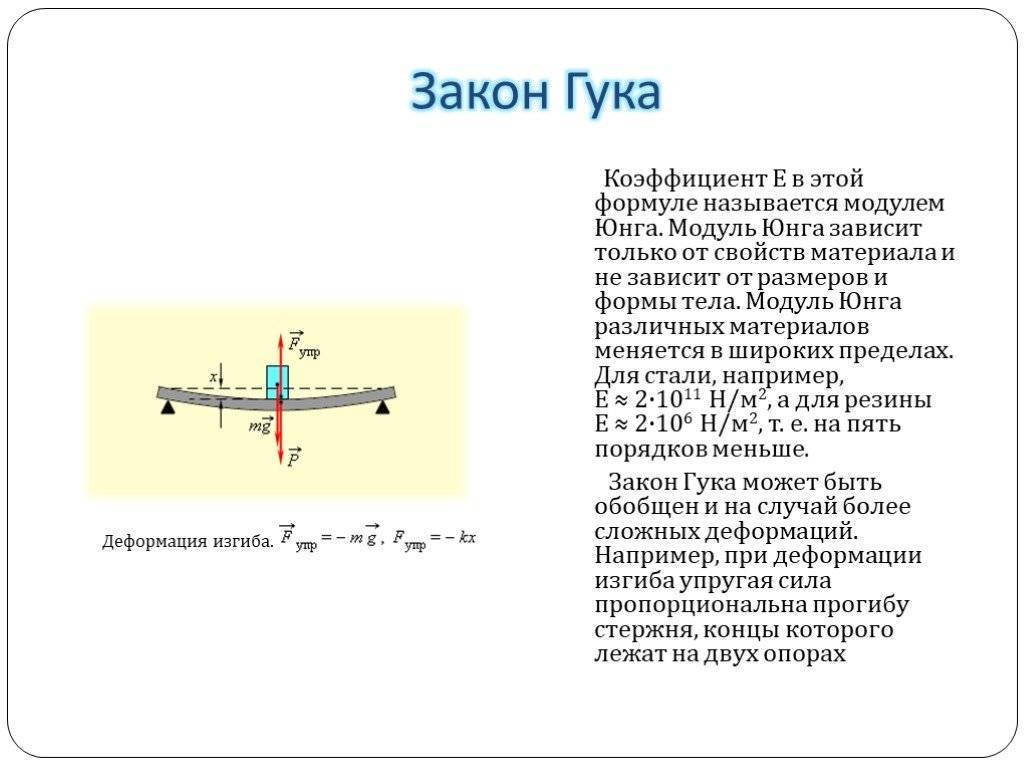
Модуль упругости (модуль Юнга) – показатель, определяющий механическую реакцию материала. При помощи данного параметра удается охарактеризовать поведение образца при растяжении. Если говорить более простым языком, то модуль упругости означает пластичные свойства стали, и чем выше показатель, тем меньше растяжение. В теории модуль Юнга обозначают буквой «Е». Это один из компонентов закона Гука, в котором рассматриваются возможные деформации упругих тел. Посредством данной величины удается связать возникающие в материале напряжения с деформацией, которую он испытывает. Единица измерения модуля упругости – паскали (Па) или мегапаскали (МПа). Однако часто инженеры при проведении расчетов отдают предпочтение кгс/см2. Показатель определяют путем исследований в лабораториях, фиксируя образцы на специальном оборудовании. В основе методики лежит разрыв образцов в форме гантелей на автоматизированных установках.

В ходе эксперимента автоматика отслеживает показатели изменения длины и натяжения заготовки, при которых она разрушается, а затем делит результаты. Полученное число и будет модулем Юнга или модулем упругости. Примечательно, что подобная методика определения показателя используется для определения Е:

• стали;
• меди;
• других упругих образцов.

В хрупких материалах параметр определяют путем сжатия до момента появления трещин. Стоит подробнее остановиться на разборе модуля Юнга с точки зрения физики. В процессе принудительного нагружения, которое приводит к изменению формы материала, внутри него возникают ответные усилия. Силы начинают оказывать сопротивление напряжениям извне и стремятся вернуть форму тела. Если образец совершенно не реагирует на нагрузку (точнее, полностью меняет форму и не восстанавливает ее при снятии усилий), его принято считать пластичным. В качестве примера стоит назвать пластилин, который наглядно отражает теорию на практике. Исследованием упругости материалов занимался ученый Р. Гук, которого интересовало, как будут меняться и удлиняться стержни разных материалов под воздействием гирь. Благодаря ранее проведенной серии опытов удалось доказать, что величины абсолютного удлинения и исходной длины прямо пропорциональны. В то же время абсолютное удлинение обратно пропорционально площади поперечного сечения исследуемого стержня.

Гук вывел целый закон, а также ввел параметр Е для характеристики свойств упругого материала. Таким образом, физический смысл модуля заключается в том, что параметр соответствует напряжению, вызываемому в стержне при растягивании на длину, которая в два раза выше при условии отсутствия видимых разрушений образца.

Посредством модуля Е удается предугадать, как будет вести себя материал при определенных нагружениях. Однако он не дает понимания того, что с ним произойдет при других способах нагружения. Поэтому для проведения эффективных расчетов необходимо введение дополнительных параметров.

• Жесткость. Показатель демонстрирует степень пластичности узла исследуемого образца. Единица измерения параметра – кгс.
• Относительное удлинение в продольном направлении. При расчете используются два показателя: величина абсолютного удлинения и общая длина образца. Показатель не имеет единицы измерения, однако для упрощенного понимания его умножают на 100%.
• Относительное удлинение в поперечном направлении. Высчитывается таким же образом, как и предыдущий параметр, только вместо длины используют диаметр стержня-образца. Как показали испытания, поперечное удлинение обычно меньше продольного.
• Коэффициент Пуассона. Представляет собой соотношение двух последних показателей. Параметр делает возможным описание того, как материал будет менять свою форму, опираясь на величину нагрузки и место ее приложения.
• Модуль сдвига. С его помощью удается описать поведение материала с упругими свойствами при воздействии сил по касательной. Другими словами, помогает оценить работу конструкции при воздействии на нее ветра под углом в 90 градусов.

Но какими симптомами обладает такая разновидность недуга?

Деформация позвоночных артерий

Заболевание этого вида – это серьезная и достаточно сложная патология. Она требует применения только комплексной разновидности подхода. Естественно, не обойтись и без тщательнейшего врачебного «расследования». Главной причиной формирования болезни принято считать шейный остеохондроз.

Деформация этого вида подразумевает под собой присутствие значительного сдавливания. В результате этого поступление требующегося количества крови в мозг в значительной степени нарушается. Обязательно бежать к врачу стоит при возникновении таких симптомов:

1. Звон, который возникает в ушах.
2. Сильное нарушение слуха.
3. Частая тошнота, которая быстро переходит во рвоту.
4. Нарушение зрения. Подобное явление чаще всего является актуальным при возникновении осложнений.

Если у вас есть симптомы описанные в этой статье, обязательно запишитесь на прием в нашу клинику.

Не занимайтесь самолечением! Даже самая маленькая проблема при неправильном лечении может значительно осложнить вашу жизнь.

Обращаясь к нам, вы можете быть уверены что:

• Получите качественную консультацию.
• Вас будут лечить врачи с многолетним опытом.
• Будет использоваться только современное оборудование и материалы.
• Вы можете получить медицинскую помощь в любой день недели. Мы работаем без выходных.

+7 (495) 120-60-89

Записаться на прием

Правило Верещагина.

Для случая, когда эпюра изгибающих моментов от заданной нагрузки
имеет произвольное, а от единичной нагрузки – прямолинейное очертание, удобно использовать графоаналитический способ, или правило Верещагина.

где A_f – площадь эпюры изгибающего момента М_f от заданной нагрузки; y_c – ордината эпюры от единичной нагрузки под центром тяжести эпюры М_f ; EI_x – жесткость сечения участка балки. Вычисления по этой формуле производятся по участкам, на каждом из которых прямолинейная эпюра должна быть без переломов. Величина (A_f*y_c) считается положительной, если обе эпюры располагаются по одну сторону от балки, отрицательной, если они располагаются по разные стороны. Положительный результат перемножения эпюр означает, что направление перемещения совпадает с направлением единичной силы (или момента). Сложная эпюра М_f должна быть разбита на простые фигуры(применяется так называемое “расслоение эпюры”), для каждой из которых легко определить ординату центра тяжести. При этом площадь каждой фигуры умножается на ординату под ее центром тяжести.

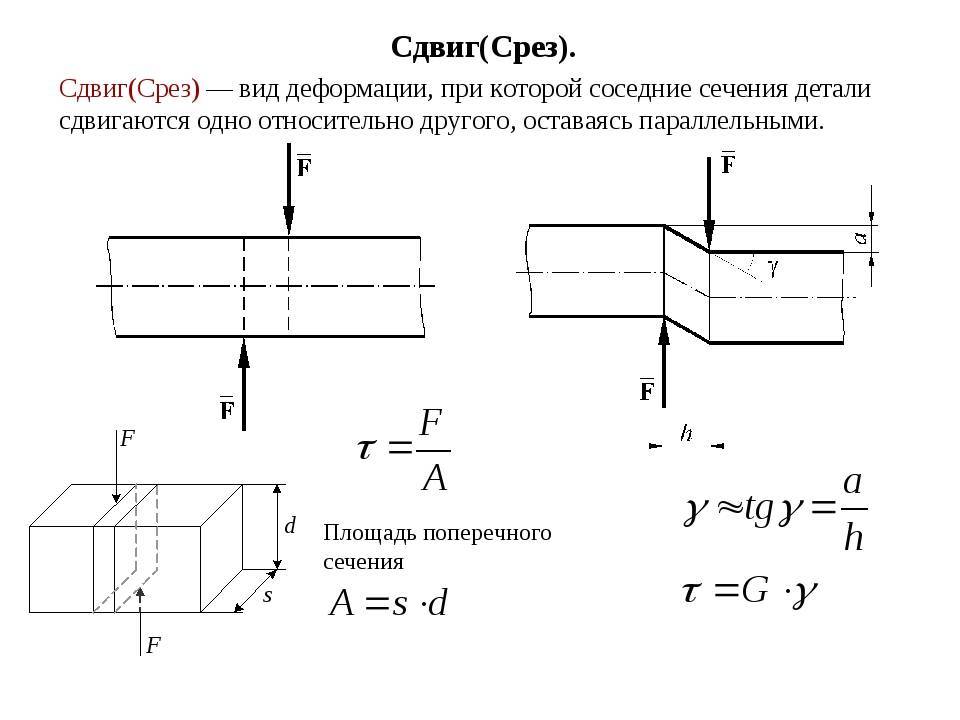
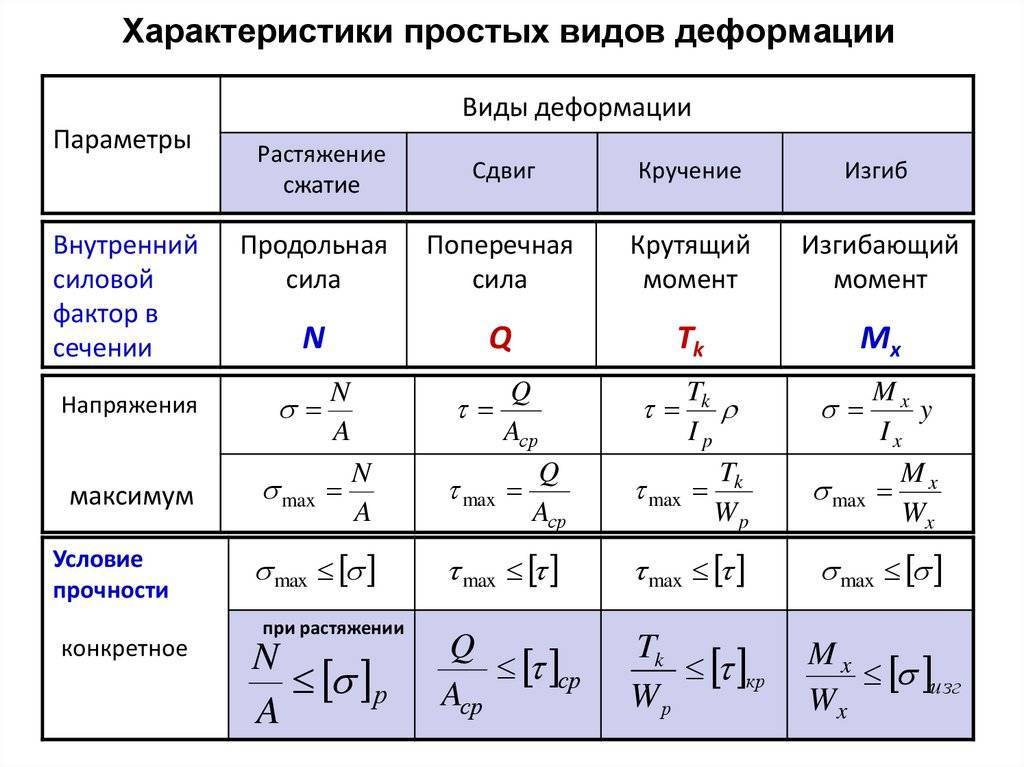
Расчёты на крепость при сдвиге

Оценка характеристик прочности изделий выполняется для определения наступления трёх факторов деформации:

1. Смещение некоторых слоёв (возникновения угла деформации).
2. Смятие крепежных элементов.
3. Сдвиг.
4. Разрыв.

Расчёт на крепость нужен для определения условий наступления любого из видов. В работе для более наглядной оценки параметров прочности и стойкости к деформированию решают существующие аналитические выражения и изображают эпюры отражающие направления влияния разных видов стрессов.

Получение численных параметров возможно благодаря использованию разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений изготавливается на основе принятых гипотез.

Расчёт возможных стрессов изготавливается на основании первой, третьей и четвёртой гипотезы прочности. Любая из гипотез принимается для различных материалов, которые обладают собственными физико-механическими свойствами.

Крепость быть на каждом из этапов разработки определенной детали. В первую очередь вычисляют величины возможных стрессов и угол отклонения на предварительном (проверочном) шаге. Это дает возможность определить их уровни, величины и направление приложенных сил. После чего приступают к проектированию. На данном шаге выполняется подбор материала детали и элементов крепежа с учитыванием достаточной прочности любого элемента конструкции. На конечном шаге ещё один раз проверяют возможные нормы нагрузки и способность готовой детали держать допустимую и дополнительную нагрузку, другими словами формируют прочностный запас.

Наиболее показательными являются расчёты для чистого сдвига. В данном случае при расчёте рассматривают следующие моменты выполнения задачи:

• Статический (составляется уравнение равновесия). В данном случае применяется предположение о равномерности распределения касательных стрессов. Впрочем в определенных случаях они делятся не одинаково, что затрудняет решение установленной задачи. Он дает возможность установить связь возникших стрессов с действующими внешними силами. Это выполняться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
• Геометрический (деформационный). Позволяет отобразить связь между отдельными маленькими участками исследуемой детали.
• Математический. Дает возможность подобрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
• Физический. Устанавливает связь между физическими процессами при деформации с учитыванием физических параметров материала и возникшими напряжениями (механическими качествами).

На математическом и физическом шаге рассмотрения установленной задачи используются следующие главные расчетные выражения и допущения:

• закон Гука для деформации смещения;
• гипотезы прочности (с учитыванием физических и механических параметров материала который для него выбран);
• выбор системы равноценных стрессов;
• упрощения при изображении эпюр, отображающих направления действующих сил и возникших стрессов;
• принятие ключевых положений для случая чистого сдвига.

В первом варианте происходит пластическая дефармация детали, когда интенсивность возникших стрессов превосходит предел текучести материала который для него выбран. Размер подобной деформации зависят от характера и интенсивности действия внешних сил, прочностных показателей материала, изменения режима температур.

При интенсивности влияния, превышающем крепость материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (к примеру, крепежных изделий, заклёпок, втулок).

Разработанные методы расчёта прочности дают возможность проектировать и делать детали с заданием, превышающим этот предел. Это дает возможность значительно повысить прочность и долговечность всей конструкции. Сейчас разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с использованием созданных программных средств, которые дают возможность получить числовые характеристики прочности и выстроить графические изображения эпюр в формате 3D графики.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

Прочность на изгиб цилиндра

Рассмотрим балку с простой опорой, у которой две равные нагрузки W / 2 действуют на расстоянии L / 3 от обоих концов.

Значение реакции в точках A и B можно рассчитать, применяя условия равновесия

Для вертикального равновесия

Принимая момент около A, момент по часовой стрелке положительный, а момент против часовой стрелки принимается как отрицательный.

Положив значение R_B в получаем

В соответствии с соглашением о знаках для ЮФО и ПРО

Сила сдвига в точке A

Сила сдвига при C

Сила сдвига в точке B

Для диаграммы изгибающего момента, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.

Изгибающий момент при A = M_A = 0

Изгибающий момент при C = [Вт / 2] * [L / 3] …………………………

Изгибающий момент при C =

Изгибающий момент при D =

Изгибающий момент при B = 0

Пусть d = диаметр цилиндрической балки, согласно уравнению Эйлера-Бернулли.