Шкала измерений

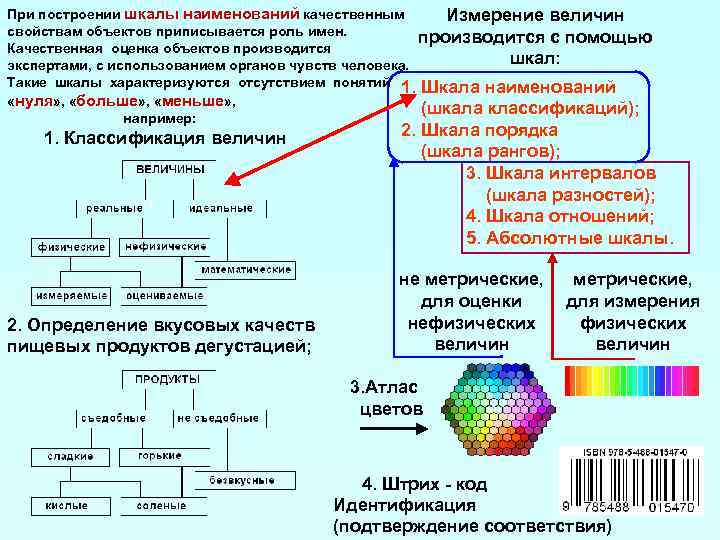
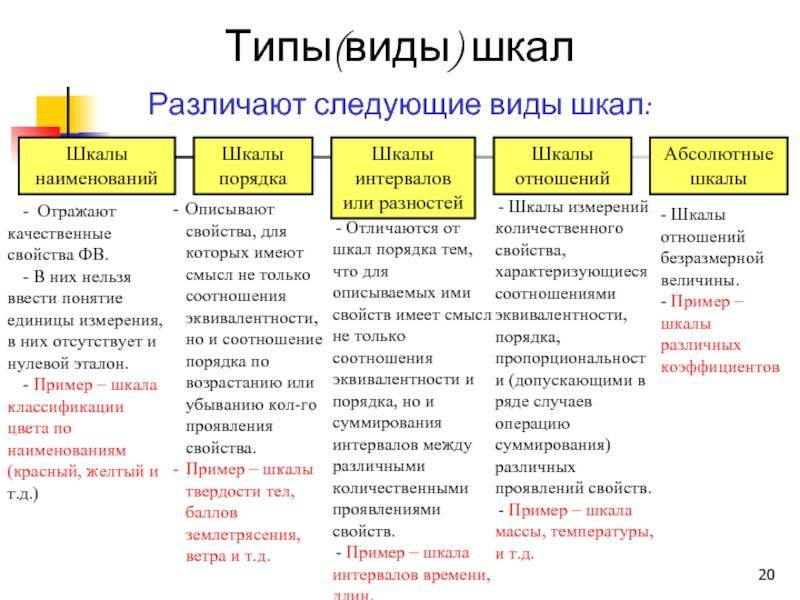
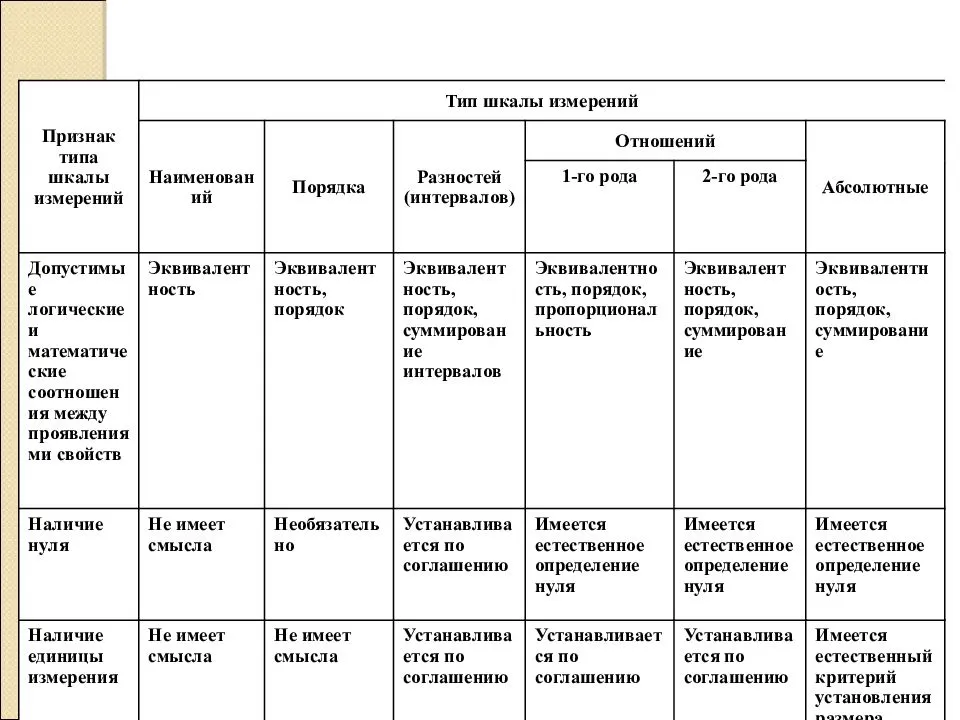
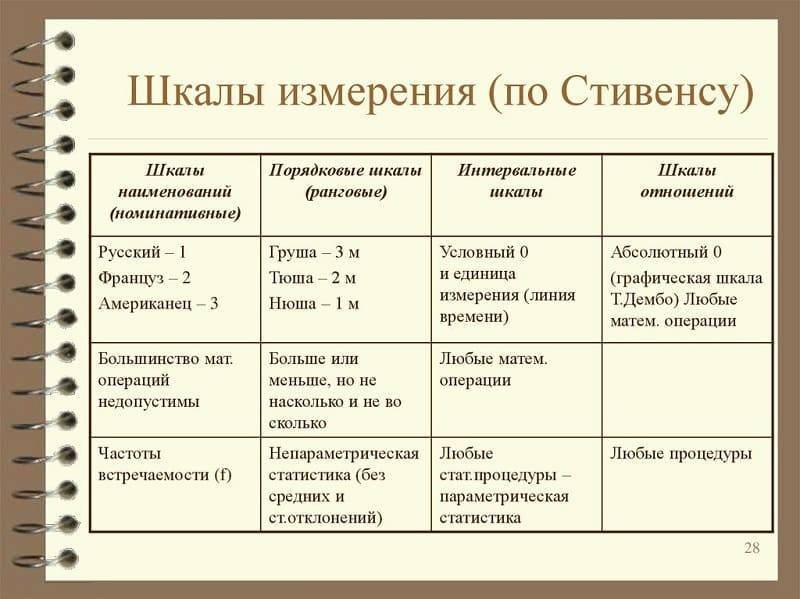
2.6.4. Относительная шкала

Шкала, в которой есть
определенная точка отсчета и
возможны отношения между значениями
шкалы. Относительные переменные очень похожи на интервальные переменные. В
дополнение ко всем свойствам переменных, измеренных в интервальной шкале, их
характерной чертой является наличие определенной точки абсолютного нуля, таким
образом, для этих переменных являются обоснованными предложения типа: X в два раза больше, чем Y. Типичными примерами шкал отношений являются
измерения времени или пространства. Например, температура по Кельвину образует
шкалу отношения, и вы можете не только утверждать, что температура 200 градусов
выше, чем 100 градусов, но и что она вдвое выше. Интервальные шкалы (например,
шкала Цельсия) не обладают данным свойством шкалы отношения. Заметим, что в
большинстве статистических процедур не делается различия между свойствами
интервальных шкал и шкал отношения.

Для этой шкалы применимы
операции: равно (=), не равно (≠), больше (>), меньше (<), сложения
(+), вычитания (-), умножения (*) и деления (/).

Относительные и
интервальные шкалы являются числовыми.

Примеры:

1)Вес
новорожденных детей 4 кг и 3 кг. Первый ребенок в 1,33 раза тяжелее второго.

2)Цена на
картофель в супермаркете в 1,2 раза выше, чем на базаре.

Интервальная шкала

Интервальная шкала обладает метрическими свойствами — она характеризуется значением интервала и допускает арифметическое сложение.
 

Интервальные шкалы часто называют шкалами высокого типа, количественными, числовыми. Смысл таких определений очевиден: числа, полученные с помощью шкал высокого типа, больше похожи на те числа, которые знакомы каждому из нас со школьной скамьи.
 

Интервальная шкала обладает также характеристикой расстояния между отдельными градациями шкалы, измеряемого с помощью определенной единицы измерений. На этой шкале оцениваются разности между отдельными градациями шкалы и можно решить, равны они или нет, а если не равны, то какая из двух больше.
 

Интервальная шкала обладает также характеристикой расстояния между отдельными градациями шкалы, измеряемого с помощью определенной единицы измерений, то есть используется количественная информация. На этой шкале уже не бессмысленны разности между отдельными градациями шкалы. В данном случае можно решить, равны они или нет, а если не равны, то какая из двух больше.
 

Они представляют собой интервальные шкалы с естественным началом.
 

Простейшим примером интервальной шкалы может служить шкала измерения температуры по Цельсию.
 

При использовании интервальной шкалы адекватным является сравнение расстояний между парами одной и той же системы.
 

Непрерывный континуум интервальной шкалы позволяет рассчитывать средневзвешенные величины, коэффициент дисперсии, характеризующий степень разбросанности признака. При этом средневзвешенные величины используются в качестве разного рода индексов, выполняющих функцию классификации, измерения и сравнения.
 

Условием применения интервальной шкалы является регулярность классов интервалов.
 

Если в интервальной шкале масштаб зафиксирован, то измерение происходит в шкале разностей. Шкала разностей допускает операции равенство-неравенство, больше-меньше, равенство-неравенство интервалов и операцию вычитания, на основе которой устанавливается величина интервала в фиксированном масштабе. К шкале разностей относятся логарифмические шкалы, а также процентные и аналогичные им шкалы измерений, задающие безразмерные величины.
 

Измерения в интервальных шкалах в известном смысле более совершенны, чем в порядковых. Применение этих шкал дает возможность не только упорядочить объекты по количеству свойства, но и сравнить между собой разности количеств.
 

Это справедливо для любых интервальных шкал.
 

Если начало в интервальной шкале является абсолютной нулевой точкой, то возникает возможность отразить в шкале, во сколько раз одно измерение отличается от другого. Соответствующая шкала называется шкалой отношений.
 

Частично-упорядоченное множество типов шкал, наиболее часто использующихся в социологических.

Наиболее типичные способы получения интервальной шкалы фактически описаны выше.
 

Измерение и качество продукции

Как уже было сказано ранее, если успешно решить вопросы, которые связаны с точностью измерения качественных параметров материалов и прочих изделий, а также поддержания режимов в технологии производства, качество продукции значительно улучшится. Если говорить простыми словами, контроль качества – это замеры всех параметров технологических процессов. Результаты их измерений нужны для управления процессом. Чем точнее результаты, тем лучше контроль.

У состояния измерений есть следующие основные свойства:

• Воспроизводимость измерительных результатов.
• Точность.
• Сходимость.
• Скорость получения.
• Единство измерений.

Воспроизводимость результатов – это близость измерительных результатов одной величины, которые были получены в различных местах, при помощи разных методов и средств, в разное время и разными людьми, но при одинаковых условиях (влажности, давлении, температуре).

Сходимость измерительных результатов – это когда результаты измерений одной величины, которые проводились повторно с помощью одних и тех же средств, тем же методом, в одних и тех же условиях, с одинаковой тщательностью, близки.

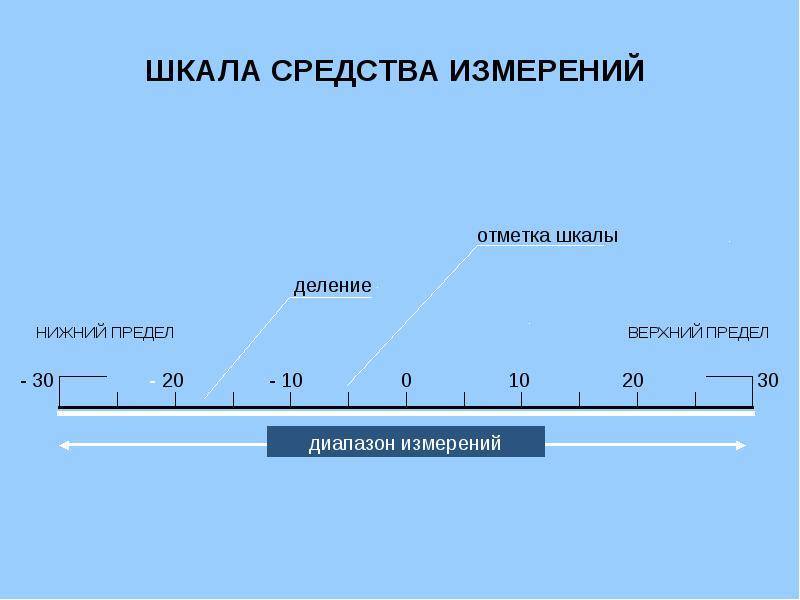
Любое измерение осуществляют с использованием соответствующих шкал.

2.2. Условия упорядоченности

Номера так же, как и числа, упорядочены; первые — произвольные образом, вторые — на основании двух отношений, существующих между упорядоченными объектами, — отношений, специальное название которых транзитивность и антисимметричность.

Транзитивность — если А находится в некотором отношении к В, а В к С, то А находится в том же отношении к С.

Симметричность — если А находится в некотором отношения к В, то В находится в том же отношении к А.

Антисимметричность — если А больше В, то В меньше А.

Отношение порядка применимо к свойству твердости: все тела, к которым применимо это понятие, связаны между собой транзитивным и антисимметричным отношением „тверже, чем» или обратным отношением „мягче, чем»; каждое тело, твердость„которого мы хотим определить, либо тверже любого другого тела того же класса, либо мягче него.

Отношение „тверже, чем» является транзитивным и антисимметричным.

Оно транзитивно потому, что если Аоставляет царапину на В, а В — на С, то Аоставляет царапину на С.

Оно антисимметрично потому, что если Аоставляет царапину на В, то Вне оставляет царапину на А.

Использование в психометрии

Основная статья: Психометрия

Используя различные шкалы, можно производить различные психологические измерения. Самые первые методы психологических измерений были разработаны в психофизике. Основной задачей психофизиков являлось то, каким образом определить, как соотносятся физические параметры стимуляции и соответствующие им субъективные оценки ощущений. Зная эту связь, можно понять, какое ощущение соответствует тому или иному признаку. Психофизическая функция устанавливает связь между числовым значением шкалы физического измерения стимула и числовым значением психологической или субъективной реакцией на этот стимул.

Шкалы и их классификации

Шкалы используются как для первичных измерений, так и для перевода разных измерений (в нашем случае — различных показателей) в единую шкалу. Как выбрать единую шкалу? Начнём с трёх определений.

Шкалой называют систему чисел или иных элементов и отношений между ними, принятых для измерения или оценки каких-либо величин (объектов, качеств и т. д.).

Шкалирование — это:

• выбор шкалы для первичных измерений;
• перевод измерения из одной шкалы в другую.

Нормирование (или единообразное шкалирование) — это перевод всех переменных, показателей, отражающих разные объекты измерений, в одну шкалу.

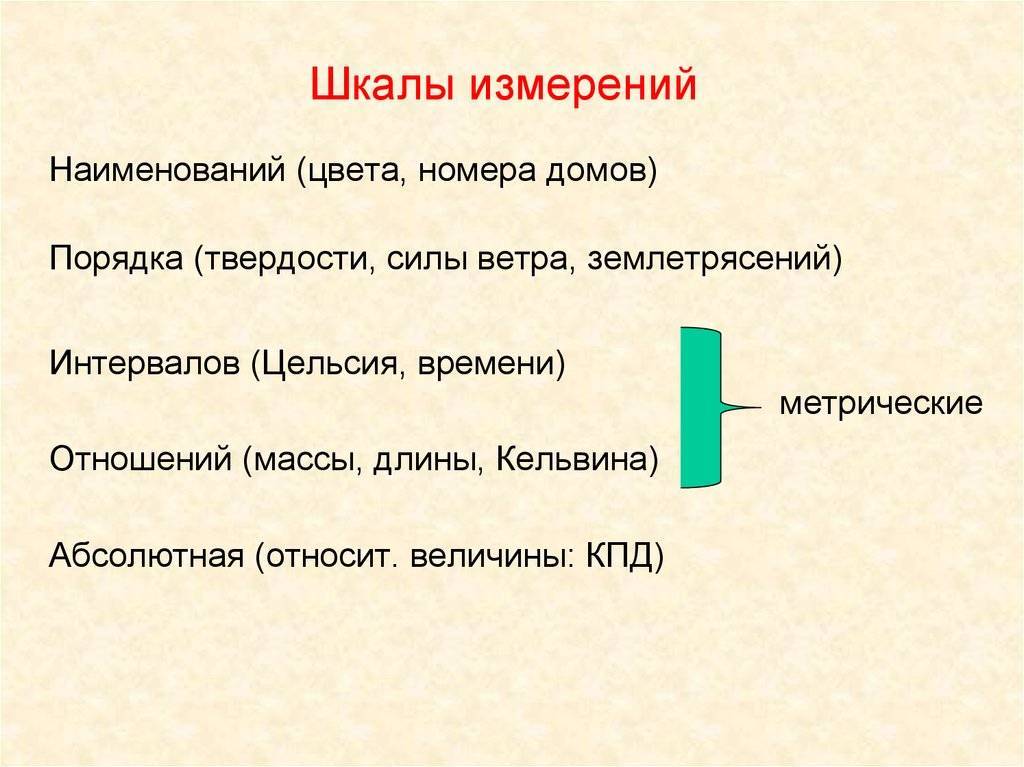
Первая классификация шкал была предложена С. Стивенсом в 1946 г. и от современной общепринятой классификации принципиально не отличается.Шкалы, как правило, объединяют в три основные группы:

• номинальные — для качественных измерений;
• порядковые — для отражения отношения порядка (больше, лучше, важнее, проще, правильнее и т. п.);
• количественные — оперируют с числами так, как мы привыкли со школьных времен (например, 10 в 2 раза больше, чем 5).

Иногда все шкалы измерения делят на два класса:

• шкалы качественных признаков (порядковая шкала и шкала наименований);
• шкалы количественных признаков (количественные шкалы).

Далее мы последовательно разберём все типы шкал.

Как считать очки в десятиборье?

Сегодня в мужском легкоатлетическом десятиборье за удачное выступление в каждом виде спорта участнику начисляется около 1000 очков. Но какой результат, по вашему мнению, берётся за 1000? Первое, что приходит на ум, — взять за 1000 очков мировой рекорд для женщин. Но какой именно? Текущий не годится, так как он меняется, а хотелось бы иметь возможность сравнений во времени и измерять рекорды. Но допустим, мы зафиксируем раз и навсегда, за что дается 1000 очков: в прыжках в длину, например, за 7,90 м, в беге на 100 метров — за 11 секунд. Далее возникает другой вопрос: какой шаг указать? Результат 8,00 м в прыжках в длину — это 1050 или 1010 очков? И как справедливо сравнивать разные виды соревнований? Думается, у каждого специалиста будут на этот счёт своё мнение и своя шкала.

Соотношение

Шкалы коэффициентов являются конечной нирваной, когда речь заходит о шкалах измерения данных, потому что они говорят нам о порядке, они говорят нам точное значение между единицами, И они также имеют абсолютный нуль, который позволяет применять широкий спектр как описательных, так и предпочтительных статистических данных.  Рискуя повториться, все, что было сказано выше о интервальных данных, относится к шкалам коэффициентов, плюс шкалы коэффициентов имеют четкое определение нуля.  Хорошими примерами переменных коэффициентов являются рост, вес и продолжительность.

Шкалы коэффициентов предоставляют массу возможностей, когда речь заходит о статистическом анализе. Эти переменные можно осмысленно добавлять, вычитать, умножать, делить (соотношения). Центральная тенденция может быть измерена по режиму, медиане или среднему значению; меры дисперсии, такие как стандартное отклонение и коэффициент вариации, также могут быть рассчитаны по шкалам коэффициентов.

Шкалы коэффициентов являются определяющей нирваной в отношении шкал оценки информации, поскольку они просветляют нас в отношении запроса, раскрывают нам точный стимул между единицами, и они также имеют прямой нуль, который принимает во внимание широкий спектр как графических, так и преимущественных представлений, которые должны быть применены. При опасности перефразировать себя, все вышеперечисленное о промежуточной информации относится к пропорционным шкалам, в дополнение к пропорционным шкалам, которые имеют безошибочное значение “ноль”

Подлинные примеры факторов пропорций включают в себя рост, вес и продолжительность.

Пропорциональные шкалы дают обилие потенциальных результатов в отношении поддающегося измерению расследования. Эти переменные могут быть значимо добавлены, вычтены, умножены, разделены (соотношения). Очаговое наклонение можно оценить по способу, середине или среднему значению; пропорции рассеяния, например, стандартное отклонение и коэффициент разнообразия также могут быть определены по шкалам пропорций.

Литература

Нормативно-техническая документация

• РМГ 29-2013 ГСИ. Метрология, Основные термины и определения
• ГОСТ 5365-83 Приборы электроизмерительные. Циферблаты и шкалы. Общие технические требования
• ГОСТ 25741-83 Циферблаты и шкалы манометрических термометров. Технические требования и маркировка

Блок: 6/7 | Кол-во символов: 391

Абсолютные шкалы

Абсолютные шкалы — это шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Примером абсолютной шкалы могут стать шкалы с относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.

Отметим, что шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений — метрическими (материальными). Метрические и абсолютные шкалы относятся к разряду линейных. Практическая реализация шкал измерений в метрологии осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.

Блок: 7/8 | Кол-во символов: 862

Изготовление измерительной шкалы своими руками

Видео о том, как самостоятельно сделать шкалу стрелочного прибора на примере изготовления шкалы амперметра.

Блок: 8/8 | Кол-во символов: 153

Кол-во блоков: 14 | Общее кол-во символов: 13188

Количество использованных доноров: 3

Информация по каждому донору:

1. https://www.lcutting.ru/content/shkaly-izmereniy: использовано 7 блоков из 8, кол-во символов 7899 (60%)
2. https://studopedia.ru/2_119506_vidi-izmereniy.html: использовано 1 блоков из 2, кол-во символов 2149 (16%)
3. https://ru.wikipedia.org/wiki/%D0%A8%D0%BA%D0%B0%D0%BB%D0%B0_%D1%81%D1%80%D0%B5%D0%B4%D1%81%D1%82%D0%B2%D0%B0_%D0%B8%D0%B7%D0%BC%D0%B5%D1%80%D0%B5%D0%BD%D0%B8%D0%B9: использовано 4 блоков из 7, кол-во символов 3140 (24%)

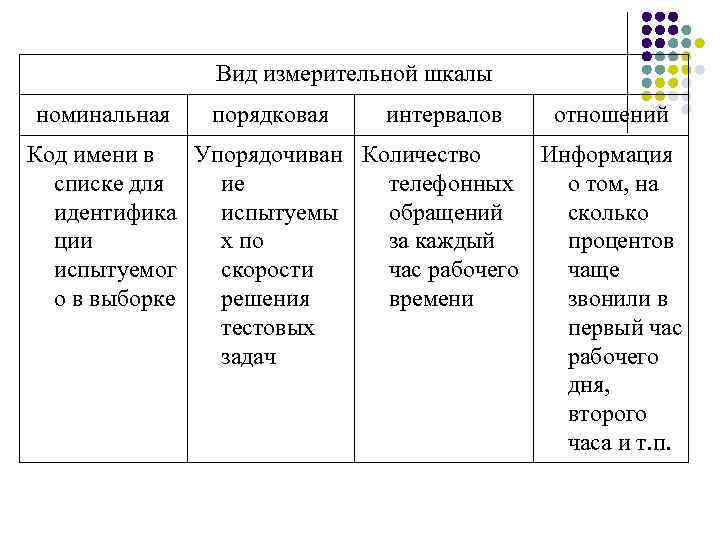
Шкалы измерений

Рассмотрим шкалы измерений подробнее.

Номинальная

Самые простые измерительные шкалы – номинальные. Они относятся к качественным и отражают те или иные свойства объекта, выраженные словесно. Их элементы могут только совпадать или не совпадать друг другом, Их нельзя сопоставлять по принципу «больше-меньше». Недопустимы также и арифметические действия.

Характерным примером может служить группа крови. Первая группа не больше третьей и не может быть сложена с четвертой. У человека может быть только одна группа крови, и измерение

Порядковая

По ней можно ранжировать и сравнивать объекты, по какому — либо признаку, например, расположить людей в строю по росту. Иванов больше Сидорова, а Сидоров больше Кузнецова.

Шкала порядка

Из этих данных можно сделать вывод о том, что Иванов выше Кузнецова, но нельзя определить, насколько именно.

Интервалов

Она состоит из заранее определенных и равных между собой интервалов. И является намного более информативной. Свойство объекта соотносится с одним из таких интервалов.

Характерным примером такой шкалы измерений может служить принятое у людей исчисление времени. Период оборота Земли вокруг Солнца делится на 365 дней, дни делятся на часы, далее на минуты и секунды. Мы можем соотнести событие с одним из таких интервалов: «эта статья была написана в 2018 году» или «Дождь начнется в 14 часов»

Шкалы интервалов

Значения в этом случае можно сравнивать друг с другом не только качественно, но и количественно, становятся доступны операции сложения и вычитания. «Заход солнца произойдет на 12 часов позже восхода». «Фильм А длиннее фильма В на 25 минут»

Однако поскольку начало отсчета не установлено, невозможно определить, во сколько раз одно значение больше другого.

Отношений

Точкой начала отсчета является точка, в которой значение параметра равно нулю. Появляется возможность отсчитывать от нее абсолютное значение параметра, определять разницы значений и во сколько раз одно больше другого. Характерный пример — температурная шкала Кельвина. За начало отчета взята точка «абсолютного нуля», при которой прекращается тепловое движение материи. Второй опорной точкой выбрана температура таяния льда при нормальном давлении. Разница между этими точками по Цельсию составляет 273 °C, и один градус Кельвина равен одному градусу Цельсия. Таким образом, можно сказать, что лед тает при 273К.

Шкала отношений

Отношений – наиболее информативная. На ней возможны все арифметические операции-

• сложение;
• вычитание;
• умножение ;
• деление.

Деление, умножение сложение и вычитание значений параметра будет иметь физический смысл. Мы можем вычислить не только насколько одно значение больше другого, но и во сколько раз.

Разностей

Представляет собой частный случай интервальных. Для них значение не меняется при произвольном числе сдвигов на определенный параметр. Другими характерными признаками являются

• единицы измерений и точка отсчета определяется по соглашению;
• существует понятие размерности;
• доступны операции линейных преобразований;
• осуществляется путем создания системы эталонов.

В качестве примера можно привести циферблат часов – каждые сутки значение времени будет, например, «7 часов», хотя это разные дни.

Циферблат часов

Другим примером может служить компас, показывающий направление из одной точки. Сама эта точка может иметь различные координаты.

Важно помнить, что в этом случае при измерении мы можем вычислять разницу между двумя значениями, но должны все время помнить о том, что начальное значении задано произвольно. Например, при переходе на летнее время придется задать новое начальное значение

Абсолютная

Абсолютная шкала занимает высшую ступень в шкальной иерархии. Единицы их естественные и не основаны на соглашениях и допущениях. Кроме того, эти единицы не имеют размерности, не служат производными системы СИ или какой-либо другой. Они всегда безразмерны:

• разы;
• проценты;
• доли;
• полные углы.

Абсолютная шкала

Абсолютные подразделяют на

• ограниченные. Диапазон от 0 до 1. Сюда относятся КПД, оптические коэффициенты поглощения т.д.
• неограниченные – предел упругости, коэффициент усиления в радиотехнике и т.д. Все они нелинейные и не имеют единиц измерений.

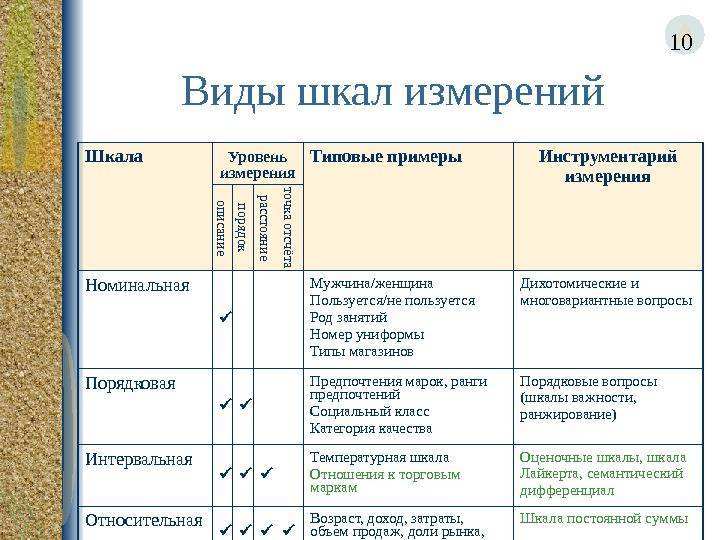
Виды шкал измерений

Суть измерения состоит в том, что текущему состоянию объекта ставится в соответствие некоторое число, порядковый номер или символ.

Что такое шкала

Совокупность таких чисел, номеров или символов и называется шкалой измерений

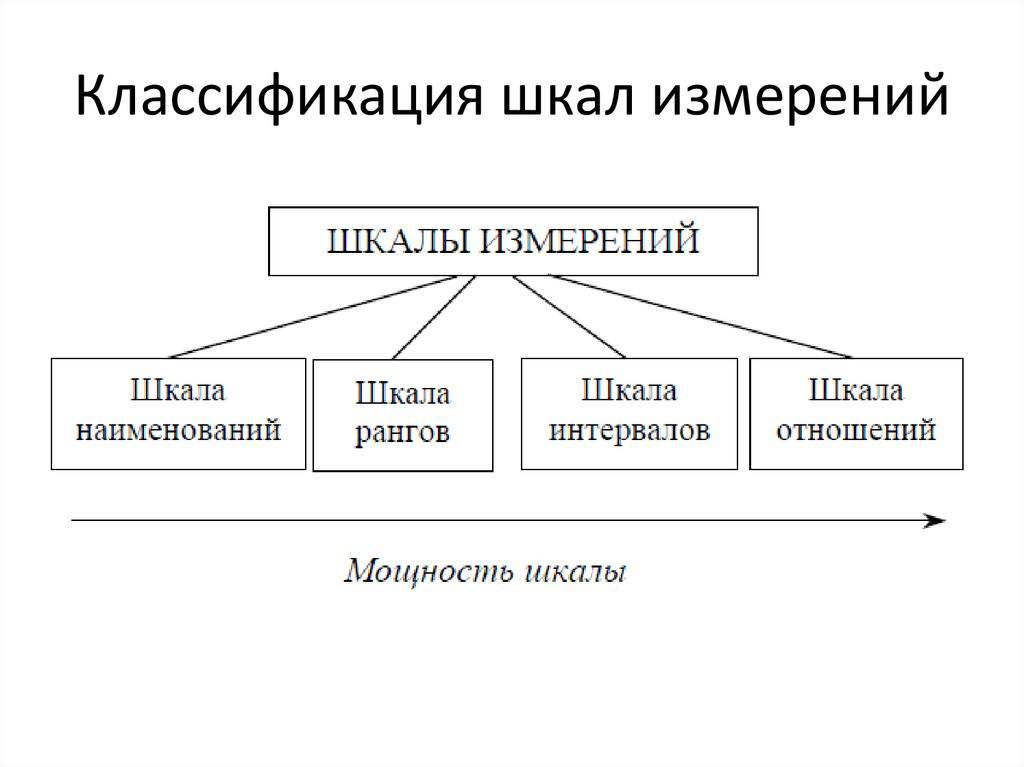
Классификация измерительных шкал

По своему типу выделяют следующие виды шкал:

• номинальная (наименований);
• порядковая;
• интервальная;
• отношений;
• абсолютная.

Шкалы также относят к одной из двух групп:

• качественные, для которых не существует единиц измерений;
  • номинальная;
  • порядковая;
• количественные, выражающие значения в определенных единицах;.
  • интервалов;
  • отношений;
  • абсолютная .

Шкалы также делятся по их силе. Чем больше сведений об объекте измерений можно извлечь из результатов измерений по ней. Самыми сильными считаются абсолютные шкалы, самыми слабыми — номинальные. Иногда исследователи усиливают шкалу, характерным примером является «оцифровка» номинальных шкал. Качественным признакам присваивают некое их числовое выражение. Это облегчает обработку результатов, особенно компьютерную

Важно помнить, что оцифровка не придает качественным признакам всех свойств, которыми обладают числа. К такой шкале можно применять операции сравнения, но нельзя — сложения, вычитания и т.п. Шкалы измерения по Стивенсу

Шкалы измерения по Стивенсу

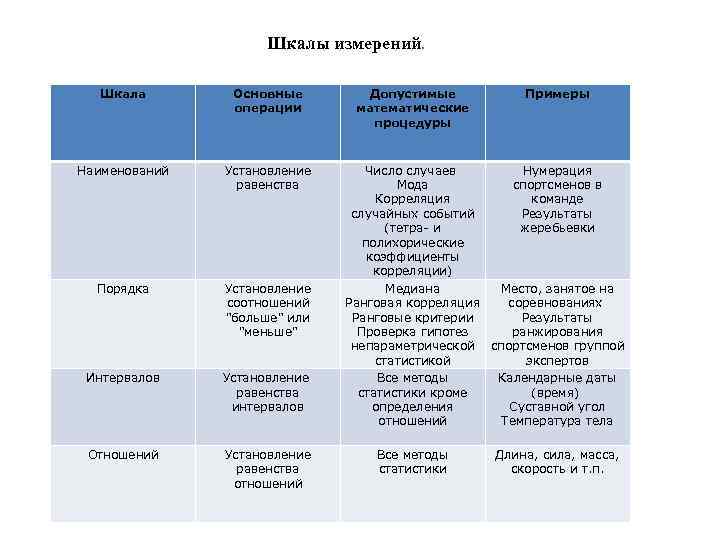
Типы шкал

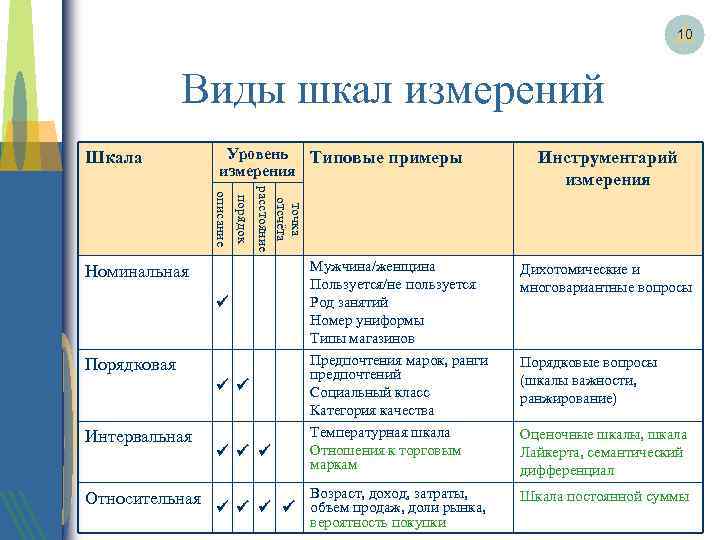
На сегодняшний день различают четыре основных типа шкал измерений: номинальная, порядковая, интервальная и относительная. Каждый тип шкалы обладает определенными признаками, которые рассматриваются ниже; сейчас же рассмотрим какую роль играет техника измерений в процессе классификации.

Часто при классификации исследователь не имеет возможности численно измерить исследуемый параметр. Например, отношение человека к чему-либо, степень его предпочтения и т.д. Способы измерения в данном случае отличаются от традиционных способов. Измерением в данном случае будет считаться любой способ приписывания числовых значений символам, которые отражают качественные характеристики объектов. При этом должны существовать устойчивые взаимосвязи между символами и качествами, которые они отражают. Иными словами, для осуществления кластеризации объекта с качественными характеристиками необходимо использовать приемы техники шкалирования.

В процессе использования техники шкал традиционно выделяют ряд стадий, качество выполнения которых оказывает непосредственное влияние на результат выделения кластеров. На первом этапе необходимо дать четкое определение тому, что собираются измерять. Далее следует указать, как измерение будет осуществлено на практике или что/кто конкретно подлежит измерению. После чего выбирают тип шкалы измерения, который предопределяет метод сбора информации. Любые измерения связаны с ошибками, но поскольку измерение в данном случае имеет специфику, то исследователь может самостоятельно оценить некоторые случайные отклонения исследуемого параметра и исключить его из кластера. Традиционно объекты наблюдения могут быть представлены в следующих типах шкал.

1 тип: номинальная или шкала наименований

Этот базовый и самый примитивный тип шкалы. При его использовании каждому объекту присваивается только идентификационный номер, как, например, номера игроков в спортивной команде, номера телефонов и т.д.

Операции в данной шкале:

2 тип: порядковая шкала

Этот тип шкалы определяет порядок или ранг объектов наблюдения. Расстояния между объектами, которые следуют друг за другом (по убыванию или по возрастанию) не являются равными. На основании результата ранжирования нельзя сказать, что расстояние между свойствами объектов и равны расстоянию между свойствами объектов и . Часто данный тип шкалы еще называют шкалой восприятия. Например, оценка качества вина по десятибалльной шкале – наиболее понравившееся качество 10 баллов, наименее – 1 балл.

Операции в данной шкале:

3 тип: интервальная шкала

В отличие от порядковой шкалы, здесь имеет значение не только порядок следования величин, но и величина интервала между ними. Пример для данного типа шкалы: температура воды в море утром – 18 градусов, вечером – 24, т.е. вечерняя на 5 градусов выше, но нельзя сказать, что она в 1.33 раз выше.

Операции, которые можно выполнять на базе этой шкалы:

4 тип: относительная или шкала отношений

В отличие от интервальной шкалы может отражать то, во сколько один показатель больше другого. Относительная шкала имеет нулевую точку, которая характеризует отсутствие измеряемого качества. Например: цена на товар. Здесь за точку отсчета можно взять «ноль» рублей. Отметим, что на практике не часто удается привести измерения к данному типу шкалы.

Операции для данной шкалы:

Примечания

1. Журавлев Ю.И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. ISBN 5-7036-0108-8.
2. ↑ Анфилатов В. С., Емельянов А. А., Кукушкин А. А. Системный анализ в управлении. — М. Финансы и статистика, 2002. — 368 с.
3. Перегудов Ф. И., Тарасевич Ф. П. Введение в системный анализ. — М.: Высшая школа, 1989. — 367 с.
4. ↑ Бахрушин В.Є. Методи аналізу даних. — Запоріжжя, КПУ, 2011
5. ↑
6. Mosteller, Frederick. Data analysis and regression : a second course in statistics (англ.). — Reading, Mass: Addison-Wesley Pub. Co, 1977. — ISBN 978-0201048544.
7. Wolman, Abel G. Measurement and meaningfulness in conservation science (англ.) // Conservation biology : journal. — 2006.
8. . Institute for Digital Research and Education. University of California, Los Angeles. Дата обращения: 7 февраля 2016.
9. Суппес П., Зиннес Д. Основы теории измерений // Психологические измерения. М.: 1967. С. 9-110.

библиография

Постановление Правительства Российской Федерации от 31 октября 2009 г. № 879 «Об утверждении Положения о единицах величин, допускаемых к применению в Российской Федерации»

РМГ83—2007 [31 И)

МБМВ. 8-е издание. 2006 (BIPM.8* Edition 2006)

Техническая запись МСВЗ.

№32

(IERS Technical Note. No. 32) (International Earth

Рекомендации no межгосударственной стандартизации. Государственная система обеспечения единства измерений. Шкалы измерений. Термины и определения Международная система единиц СИ (The international System of Units SI. Pans)

Международная службе вращения Земли и опорных систем. Соглашения МСВЗ (2003)

Rotation and Reference Systems Service. IERS

Conventions (2003))

(5) Постановление Правительства Российской Федерации от 28 июля 2000 г. № 668 «Об установлении единых государственных систем координат»

(6) Распоряжение Правительства Российской Федерации от 20.06.2007 г. № 797-р

(7) Постановление Правительства Российской Федерации от 3 марте 2007 г. № 139 «Об утверждении Правил установления местных систем координат»

14

ГОСТ P 8.69ft—2010

УДК 53.081:006.354 ОКС 17.020 Т80 ОКСТУ 0008

Ключевые слова: глобальная навигационная спутниковая система, величины, единицы измерения, шкалы величин, шкалы измерений, шкалы времени, координаты, системы координат

15

Редактор Л.В. Афанасенко Технический редактор И.С. Гришемоеа Корректор U.B. Вучная Компьютерная верстка В.И. Грищенло

Сдано а набор 28.04.2010. Подписано а печать 08.06.2010. Формат 60×84’/•. Бумага офсетная. Гарнитура Ариал. Печать офсетная. Уел. печ. п. 2.32. Уч.-иад. л. 2.00. Тираж 111 экэ. Зак. 460.

. 123995 Москва. Гранатный лер.. 4. info^goalinfo.iu Набрано во на ПЭВМ

Отпечатано е филиале — тип. «Московский печатник». 105062 Москва. Лялин лер.. 6

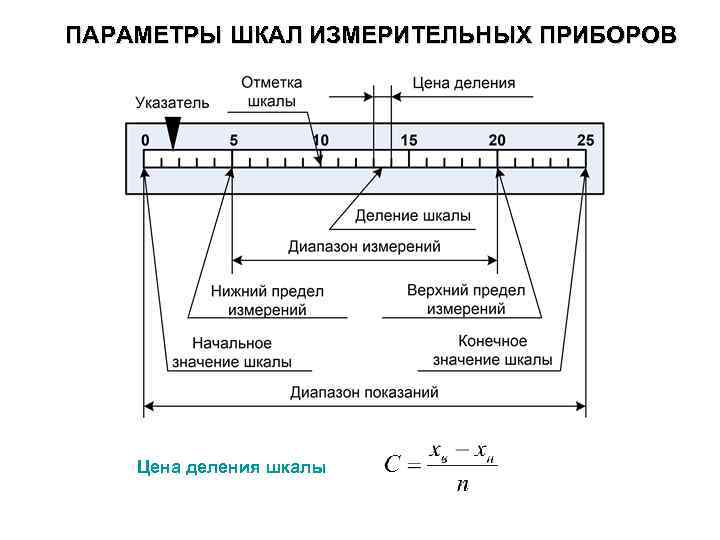
Свойства шкал

Неравномерная шкала омметра

• Начальное значение шкалы — наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений. Во многих случаях шкала начинается с нулевой отметки, однако могут быть и другие значения — например, у медицинского термометра это 34,3 °C.
• Конечное значение шкалы — наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.
• Характер шкалы — функциональная зависимость a = f(x) между линейным (или угловым) расстоянием a какой-либо отметки от начальной отметки шкалы, выраженным в долях всей длины шкалы, и значением x измеряемой величины, соответствующим этой отметке:
  • Равномерная шкала — шкала, отметки на которой нанесены равномерно.
  • Неравномерная шкала — шкала, отметки на которой нанесены неравномерно.
  • Логарифмическая или гиперболическая шкала — шкала с сужающимися делениями, характеризуемыми тем, что отметка, соответствующая полусумме начального и конечного значений, расположена между 65 и 100 % длины шкалы. Следует заметить, что выражение «логарифмическая шкала» используется и по отношению к другому значению понятия «шкала» (см.: Шкала физической величины, Логарифмический масштаб).
  • Степенная шкала — шкала с расширяющимися или сужающимися делениями, но не подпадающая под определение логарифмической (гиперболической) шкалы.

Шкала интервалов (разностей)

Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов — летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.

Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)

На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.

Шкала интервалов величины Q описывается уравнением Q = Qо + q, где q — числовое значение величины; Qо — начало отсчета шкалы;  — единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Qо шкалы и единицы данной величины .

Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1 ~ Qо) — основным интервалом. Точка Qо принимается за начало отсчета, а величина (Q1 -Qо)/n= за единицу Q. При этом n выбирается таким, чтобы было целой величиной.

Рисунок – Пример шкалы отношений

При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.

Шкала отношений

Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Пример шкалы отношений — шкала массы (второго рода), термодинамической температуры (первого рода).

В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета

К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин

Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)

Шкалы отношений — самые совершенные. Они описываются уравнением Q = q, где Q — ФВ, для которой строится шкала, — ее единица измерения, q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1/.

Порядковые шкалы

Порядковая шкала отражает более высокий уровень измерений, учитывающий, к какой категории принадлежит объект и в каком отношении он находится с другими объектами. В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между ними.Пример. Простейшим примером порядковой шкалы служат оценки знаний учащихся. Символично, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе тот же смысл выражается словесно — «неудовлетворительно», «удовлетворительно», «хорошо», «отлично». Этим подчёркивается «нечисловой» характер оценок знаний студентов.Фактически измерение по порядковой шкале представляет собой операцию упорядочения. Предполагаются сравнения «больше — меньше» или «лучше — хуже». Например, мнения экспертов часто выражаются в порядковой шкале, то есть эксперт может сказать (и обосновать), что один показатель качества продукции важнее, чем другой; первый технологический объект опаснее, чем второй, и т. д. Но он не в состоянии сказать, во сколько раз или насколько он более важен, или, соответственно, более опасен.Допустимые преобразования. Порядковая шкала допускает любое возрастающее преобразование, то есть такое, которое не меняет порядок шкалы.Типы порядковых шкал. Используют два типа порядковых шкал, которые различны с практической точки зрения:

• ранговая шкала, которая предполагает присвоение объектам рангов (ранжирование);
• балльная шкала, в которой применяются баллы.

Обдумывание измерений некоторых показателей следует начать с выбора между ранговым и балльным типами шкал.

Примеры

• Шкала атомного длина метра и определяется размером атома водорода ( то есть , то радиус Бора (приблизительно 53  мкм )) , который устанавливается с помощью электрона комптоновского длины волны раза в постоянной тонкой структуры : . ℓ а ∼ 10 — 10 { displaystyle ell _ {a} sim 10 ^ {- 10}} ℓ а ∼ 1 / α м е { displaystyle ell _ {a} sim 1 / alpha m_ {e}}
• Масштаб длины для сильных взаимодействий (или полученный из КХД посредством пространственной трансмутации ) составляет около метров (или в натуральных единицах 1000 МэВ или 1 ГэВ), а «радиусы» сильно взаимодействующих частиц (таких как протон ) примерно равны сопоставимы. Этот масштаб длины определяется диапазоном потенциала Юкавы . Время жизни сильно взаимодействующих частиц, таких как ро-мезон , дается этой шкалой длины, деленной на скорость света: секунды. Массы сильно взаимодействующих частиц в несколько раз превышают соответствующий энергетический масштаб (от 500 МэВ до 3000 МэВ). ℓ s ∼ 10 — 15 { displaystyle ell _ {s} sim 10 ^ {- 15}} 10 — 23 { displaystyle 10 ^ {- 23}}
• Шкала электрослабой длины короче, примерно в метрах, и определяется массой покоя слабых векторных бозонов, которая составляет примерно 100 ГэВ. Этот масштаб длины будет расстоянием, на котором сила Юкавы передается через слабые векторные бозоны. Величина слабой шкалы длины первоначально определялась константой Ферми, измеренной по распадам нейтронов и мюонов . ℓ ш ∼ 10 — 18 { displaystyle ell _ {w} sim 10 ^ {- 18}}
• Длина Планка (масштаб Планка) намного короче , пока — около метра ( ГэВ в естественных единицах), и происходит от Ньютона гравитационной постоянной , которая имеет единицы длины в квадрате. ℓ п ∼ 10 — 35 год { displaystyle ell _ {P} sim 10 ^ {- 35}} 10 19 { displaystyle 10 ^ {19}} — 1 { displaystyle ^ {- 1}}
• Мезоскопическая шкала представляет собой длину , при которой квантовые поведения в жидкости или твердого тела можно описать с помощью макроскопических понятий.