Эвольвентное зубчатое зацепление

Определение усилий в кинематических парах

. На первом этапе вычисляем значения равнодействующих систем сил:

.
Вычерчиваем наиболее удаленную группу Ассура (звенья 5 и 4), с сохранением всех
геометрических размеров.

На
группу Ассура начерченную дополнительно помимо сил реакции связей наносят
направления линейных ускорений центров масс, угловых ускорений и
равнодействующих соответствующих систем сил используя план ускорений. Сила P₅₄ – действие звена 5 на звено 4, P₃₄ – действие звена 3 на звено 4.

Выполнив
выше описанное, записываем уравнение моментов для 4-ого и 5-ого звеньев
относительно точки С, используя теорему Вариньона:

Так как используется графический метод для решения последнего уравнения
необходимо ввести масштаб сил

Строем план сил и находим неизвестные величины:

4. Рассмотрим звенья 3 и 2. Вычерчиваем группу Ассура с сохранением всех
геометрических размеров.

На группу Ассура начерченную дополнительно помимо сил реакции связей
наносят направления линейных ускорений центров масс, угловых ускорений и
равнодействующих соответствующих систем сил используя план ускорений. Cила Р₄₃ – действие звена 3
на звено 4, сила P₃₂ – действие звена 2 на звено 3.
Записываем уравнение моментов для 2го звена относительно точки A, используя теорему Вариньона:

|

Так как используется графический метод для решения последнего уравнения
необходимо ввести масштаб сил К=279 Н/мм

Строем
план сил и находим неизвестные величины:

. Рассмотрим кривошип 1, для чего вычертим его с сохранением
геометрических размеров. P₂₁ – давление шатуна 2 на кривошип 1,
так как центр масс лежит на оси вращения О (кривошип уравновешен), то уравнение
сил будет иметь вид:

Выполнив второй лист курсового проекта произвел исследование
шарнирно-рычажного механизма. Выполнил кинематический и динамический анализ
механизма, графическим методом при помощи плана скоростей, ускорений и сил,
нашёл соответственно скорости, ускорения точек механизма и возникающие в
кинематических парах усилия.

Исследование кривошипно-ползунного механизма

Исходные данные

lOA=	0.1 м
lAB=	0.45 м
lAS2=	0.15 м
n*=	700 об/мин
KL=	0.002 м/мм
Ki=	15000 Па/мм
D=	0.15 м
d=	0.0 м
m2=	3.84кг
m3=	5.0 кг
=0.00625

Заключение

Данный курсовой проект по теории машин и механизмов является первой
самостоятельной расчетно-графической работой в процессе обучения в
университете. Он научил нас самостоятельно решать инженерные задачи, связанные
с анализом и синтезом механизмов.

В графической части проекта были спроектированы три механизма: зубчатый
механизм, где производилось исследование эвольвентного зацепления зубьев и
проектирование зубчатой передачи из условия получения наименьших её габаритов и
определение некоторых характеристик этой передачи; шарнирно – рычажный
механизм, где производился кинематический и динамический анализ конкретного
плоского шарнирно-рычажного механизма и кривошипно-ползунный механизм, для
которого были построены графики скорости и ускорения поршня, силы давления на
поршень, силы действующей на палец шатуна и моментов, действующих на кривошип.

В расчетно-пояснительной записке был произведен расчет характеристик
обоих механизмов. В исследовании эвольвентного зацепления зубьев мы нашли
наименьшее число зубьев и определили скорости скольжения зубьев. В исследовании
шарнирно-рычажного механизма мы определили скорости, угловые скорости,
ускорения, угловые ускорения звеньев механизма и усилия в кинематических парах.

В целом нами была произведена объемная работа, и знания, полученные нами
в ходе её выполнения, пригодятся в процессе дальнейшего обучения в
университете.

Список
литературы

. Исследование шарнирно-рычажных механизмов: Метод. Указания
к курсовому проектированию / Казан. гос. технол. ун-т; Сост.: Б.В. Крапоткин,
А.Г. Замалиев. Казань 2008. – 52 с.

. Методические указания к выполнению первого раздела
курсового проекта «Исследование эвольвентного зацепления» / Казан. гос. технол.
ун-т; Сост.: Б.В. Крапоткин, А.Г. Замалиев. Казань 1987. – 20 с.

. Артоболевский И.И. теория машин и механизмов: Учеб. Для
втузов. – 4-е изд., перераб. И доп. – М.: Наука, 2005. – 640 с.

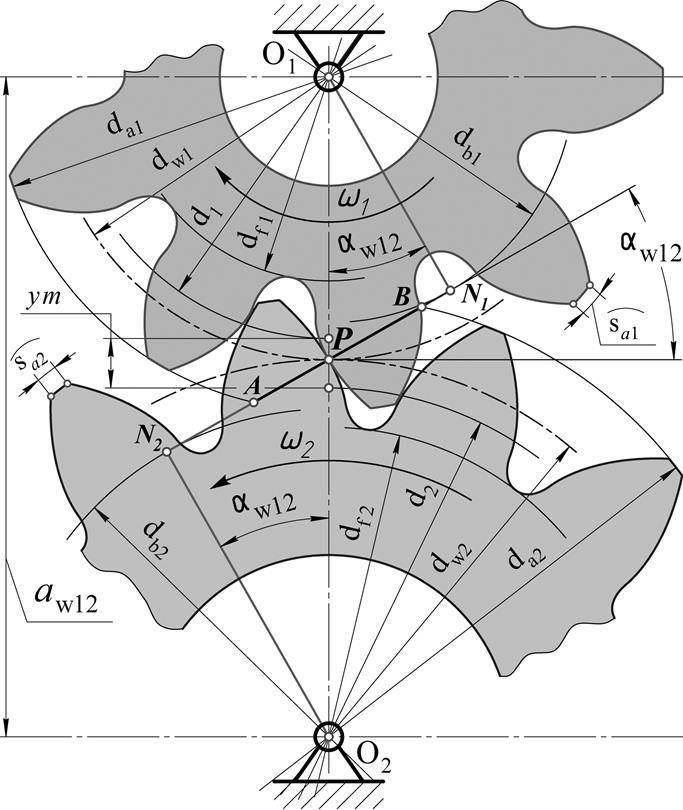
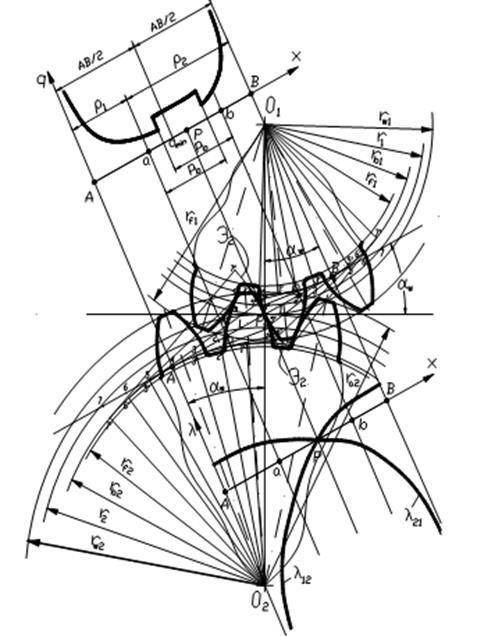
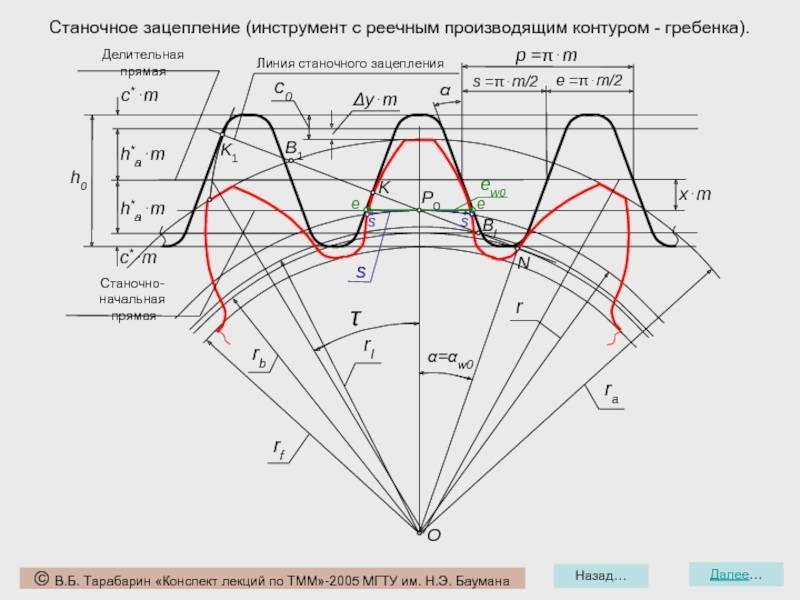
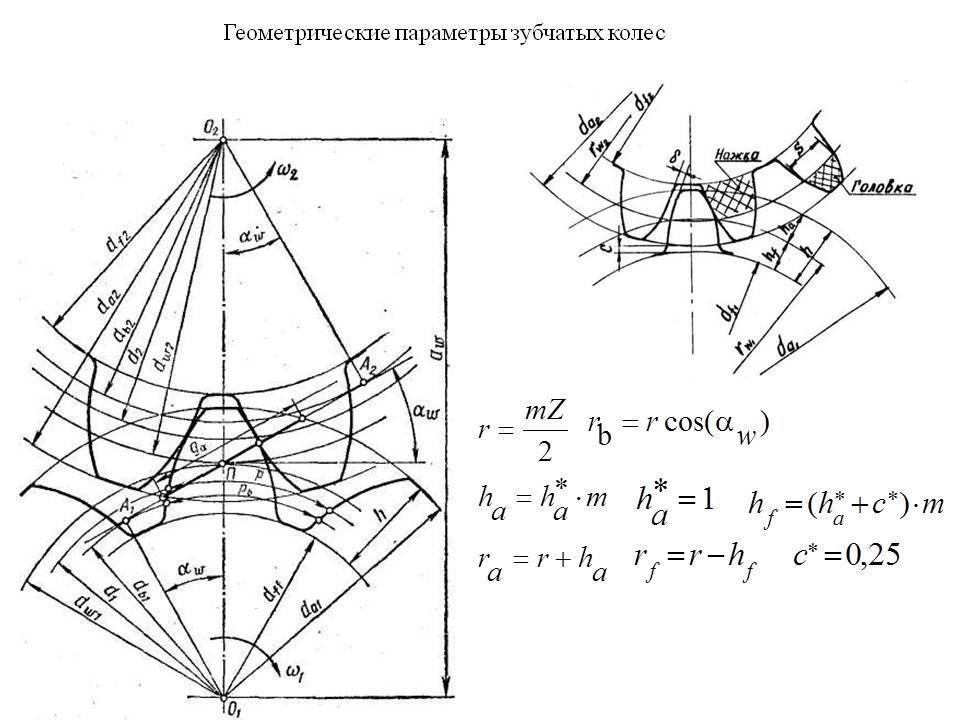
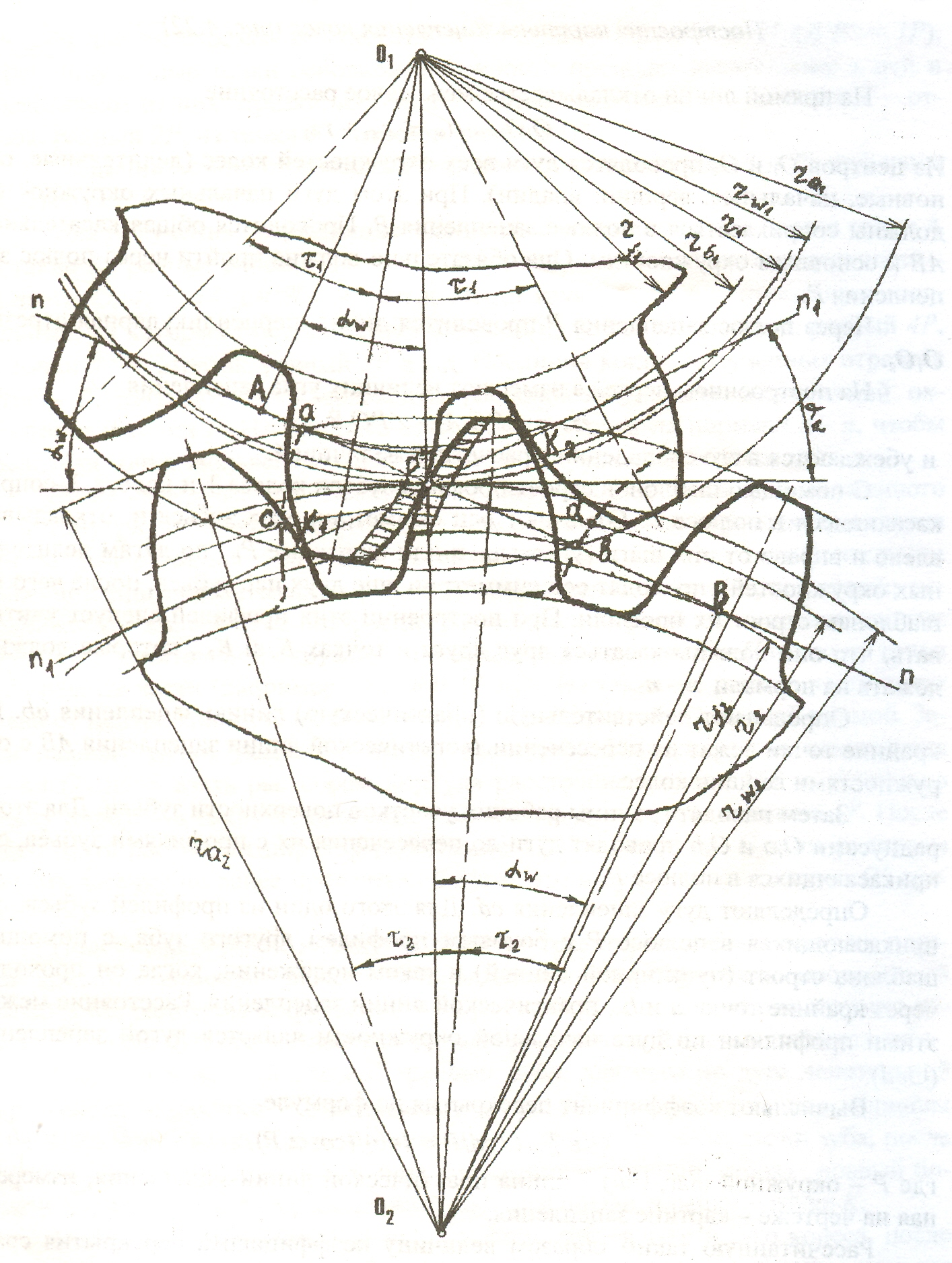
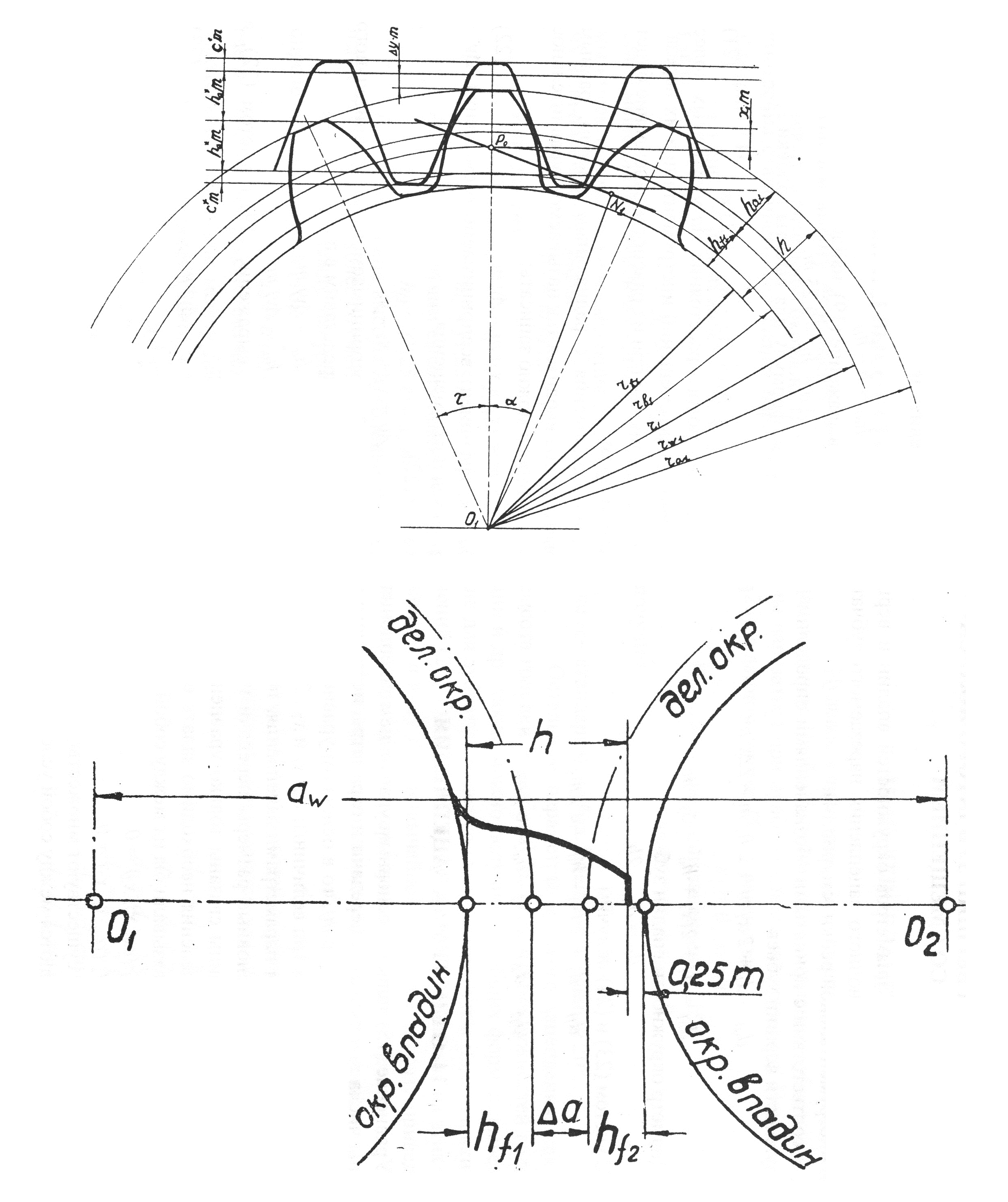
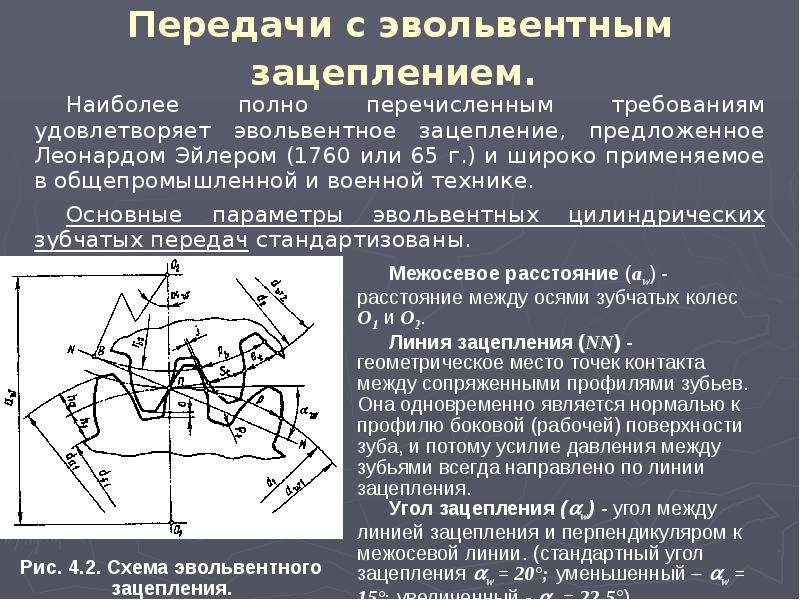
Построение эвольвентного зацепления

Способ приближённого построения эвольвентного зубчатого зацепления. Подходит для технических рисунков, построенных от руки или с помощью САПР.

Перед построением необходимо задать следующие размеры:

• высота ножки зуба hf{\displaystyle h_{f}} (на рис. обозначена a);
• высота головки зуба ha{\displaystyle h_{a}} (на рис. обозначена b);
• диаметр начальной окружности dw{\displaystyle d_{w}} (на рис. обозначен D);
• угол зацепления α{\displaystyle \alpha } (на рис. обозначен φ);
• окружная толщина зуба s_t;
• радиус кривизны переходной кривой в граничной точке профиля ρ_f.

	Изобразите начальную окружность (pitch circle) с диаметром D, и центром шестерни O. Окружность показана красным цветом. Изобразите окружность вершин зубьев (outside diameter) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета). Изобразите окружность впадин зубьев (root diameter) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета).
	Проведите касательную к начальной окружности (розовая). В точке касания под углом φ проведите линию зацепления (line of action), оранжевого цвета. Изобразите окружность, касательную к линии зацепления, с центром в точке O. Эта окружность является основной (base circle) и показана синим цветом.
	Отметьте точку A на окружности вершин зубьев. На прямой соединяющие точки A и O отметьте точку B находящуюся на основной окружности. Разделите расстояние AB на 3 части и отметьте точкой C полученное значение от точки A в сторону точки B на отрезке AB.
	От точки C проведите касательную к основной окружности. В точке касания отметьте точку D. Разделите расстояние DC на четыре части и отметьте точкой E полученное значение от точки D в сторону точки C на отрезке DC.
	Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба (показана оранжевым цветом). Изобразите дугу окружности с центром в точке C и радиусом, равным толщине зуба. Место пересечения с начальной окружностью (pitch circle) отметьте точкой F. Эта точка находится на другой стороне зуба.
	Изобразите скругление (fillet) между стороною зуба и окружностью впадин зубьев (root diameter). Изобразите радиус профиля зуба — дугу окружности радиусом EC из точки F (отмечено темно зеленым). Отметьте место пересечения радиуса профиля зуба с основной окружностью точкой G (точка G на изображении показана не верно)
	Изобразите радиус профиля зуба — дугу окружности радиусом EC из точки G — это другая сторона зуба. Добавьте скругление у основания зуба к окружности впадин зубьев (как в предыдущем шаге)
	Зуб готов. Наружная окружность между двумя боковыми поверхностями – это вершина зуба. Повторите операцию для каждого зуба.

Перед построением эвольвентного зацепления необходимо рассчитать его геометрические параметры. Предположим, что даны числа зубьев колеса z1{\displaystyle z_{1}} и шестерни z2{\displaystyle z_{2}}, указан тип зацепления: нулевое, равносмещенное или неравносмещенное. Сначала исходя из типа по таблицам или блокирующему контуру нужно выбрать коэффициенты смещения x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}.

Формула изобретения

1. Зубчатое колесо смешанного или эвольвентного зацепления с торцовым профилем зубьев, содержащим эвольвентные участки или, в сочетании, эвольвентные и неэвольвентные участки с образованием в парном зацеплении по эвольвентным участкам угла зацепления _tw, отличающееся тем, что в парном зацеплении реализует угол зацепления эвольвентных участков _tw, выбранный из условия взаимозаменяемости с заменяемым, например ремонтируемым, эвольвентным колесом, отличным по его значению от угла зацепления заменяемого колеса в его парном зацеплении _tw°, и/или образует в окрестности, как минимум, одной из фаз торцового пересопряжения зубьев участки с выпукло-вогнутыми торцовыми профилями зубьев, при этом значения коэффициентов торцового и суммарного перекрытия зубьев уменьшены соответственно относительно номинальных коэффициентов перекрытия ° и ° заменяемого колеса в его парном зацеплении вплоть до <1 и <1, а неэвольвентные участки выполнены с отклонениями в сторону утолщения зуба относительно эвольвентного профиля.

2. Зубчатое колесо эвольвентного зацепления по п.1, отличающееся тем, что число его зубьев выбрано меньшим числа зубьев заменяемого зубчатого колеса, а в парном зацеплении оно образует увеличенный угол зацепления _tw>_tw° из условия уменьшения значения коэффициента торцового перекрытия <° как _min, где 1,04 _min 1,1.

3. Зубчатое колесо эвольвентного зацепления по п.1, отличающееся тем, что число его зубьев выбрано большим числа зубьев заменяемого зубчатого колеса, а с парным, предельно изношенным колесом оно образует зацепление с уменьшенным углом зацепления _tw<_tw° из условия увеличения значения коэффициента торцового перекрытия относительно фактического значения коэффициента торцового перекрытия заменяемого колеса в его парном зацеплении _f°·> _f° как _max, где 1,04 _max 1,3.

4. Зубчатое колесо смешанного зацепления по п.1, отличающееся тем, что максимальные значения отклонений каждого выпуклого неэвольвентного участка зубьев от эвольвентного торцового профиля примерно равны максимальным величинам глубины износа по соответствующим участкам, а их текущие значения монотонно, по мере удаления от точки максимума, уменьшаются относительно глубины износа в соответствующих точках каждого участка зубьев неравномерно изношенного парного колеса.

5. Зубчатое колесо смешанного зацепления по п.1, отличающееся тем, что минимальные значения отклонений зубьев каждого вогнутого неэвольвентного участка от эвольвентного торцового профиля примерно равны минимальным величинам глубины износа по соответствующим участкам, а их текущие значения монотонно, по мере удаления от точки минимума, увеличиваются относительно глубины износа в соответствующих точках каждого участка зубьев неравномерно изношенного парного колеса.

6. Зубчатое колесо смешанного зацепления по п.1, отличающееся тем, что боковая сторона торцового профиля зубьев содержит два неэвольвентных участка у головки зуба с кривизной разного знака и с точкой перегиба примерно соответствующей точке максимальной глубины износа парного колеса, и неэвольвентный участок у ножки зуба, описанный вогнутыми кривыми с возрастающими к основанию зубьев отклонениями от эвольвентного профиля.

7. Зубчатое колесо по п.1, отличающееся тем, что боковая сторона торцового профиля зубьев содержит соединенные между собой малоразмерным технологическим участком два эвольвентных участка – участок у головки зубьев с большим радиусом основной окружности, и участок у ножки зубьев с меньшим радиусом основной окружности, выполненные с отклонениями в сторону утолщения зубьев относительно номинального профиля заменяемого колеса, возрастающими к их верхней граничной точке у головки зуба и к нижней граничной точке у ножки зуба.

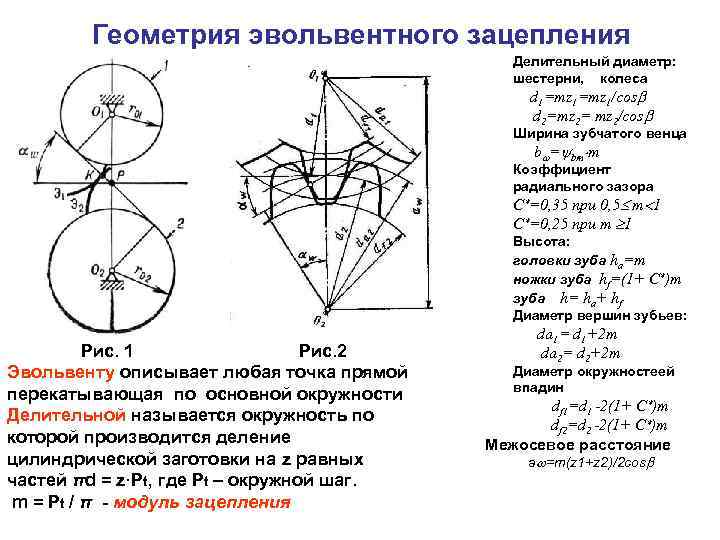
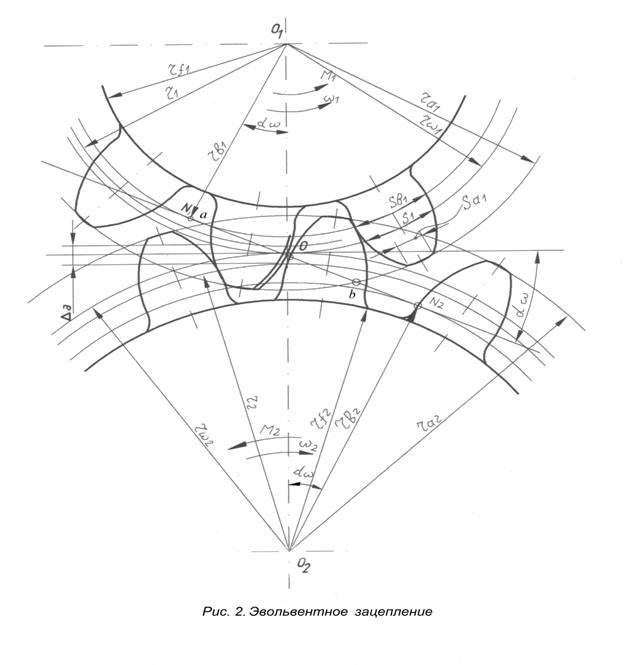
Эвольвентное зацепление

Эвольвентное зацепление, как внешнее, так и внутреннее, допускает изменение межосевого расстояния с сохранением ранее предусмотренного передаточного отношения.
 

Эвольвентное зацепление ( качение прямой) предпочтительнее, так как некоторое изменение во взаимном расстоянии валов не отражается на работе трансмиссии, и так как образованные таким образом зубья имеют наибольшую ширину у своего основания в месте сопряжения с телом шестерни; это обстоятельство позволяет им хорошо сопротивляться действию усилий, передающихся при соприкасании зубьев.
 

Эвольвентное зацепление также имеет некоторые недостатки, которые начинают выявляться в современных мощных передачах

В связи с этим особое внимание уделяется внутреннему эвольвентному зацеплению, где происходит соприкасание выпуклых и вогнутых профилей зубьев.
 . Эвольвентное зацепление, как внешнее, так и внутреннее, допускает изменение межосевого расстояния с сохранением ранее предусмотренного передаточного отношения.
 

Эвольвентное зацепление, как внешнее, так и внутреннее, допускает изменение межосевого расстояния с сохранением ранее предусмотренного передаточного отношения.
 

Образование эвольвентных профилей.

Эвольвентное зацепление малочувствительно к отклонениям межосевого расстояния. Эволь-вентные зубчатые колеса могут нарезаться простым инструментом, имеющим прямолинейный профиль зубьев, и они удобны для контроля.
 

Эвольвентное зацепление обладает технологическими и эксплуатационными достоинствами; эвольвентные зубья могут быть нарезаны простым инструментом, причем одним инструментом можно нарезать колеса с разным числом зубьев; правильность эвольвентного зацепления не нарушается при изменении межосевого расстояния; рабочий профиль зубьев в эвольвентном зацеплении может быть исправлен, что приводит к обеспечению наилучшей работоспособности, повышению КПД и других характеристик.
 

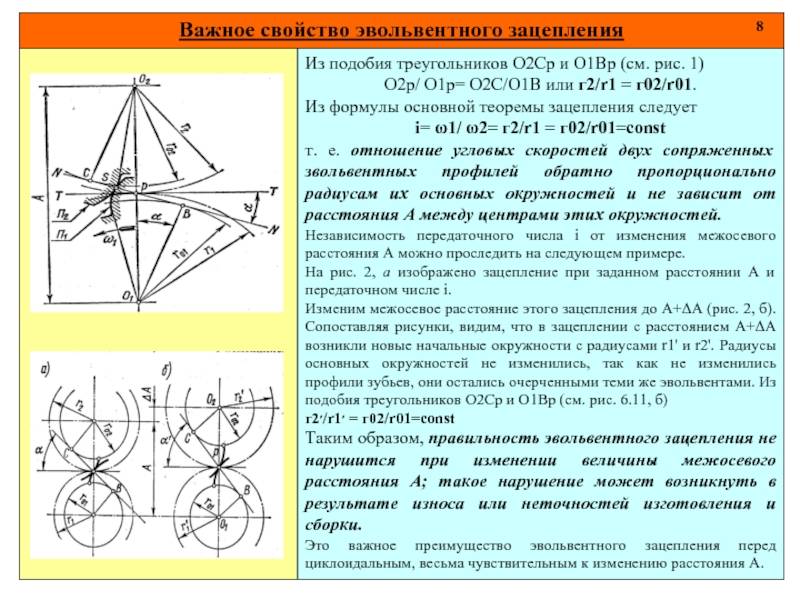
Эвольвентное зацепление нашло преимущественное применение в приборе – и машиностроении благодаря простоте образования профиля, а также тому обстоятельству, что на правильность зацепления не оказывает влияния изменение межцентрового расстояния, как это имеет место при всех разновидностях циклоидального зацепления. Здесь боковая поверхность зубьев по всей их рабочей высоте очерчивается эвольвентой, поэтому линия зацепления ( траектория движения точек касания зубьев двух колес – линия р Pz на рис. 38) есть прямая, касательная к основным окружностям с радиусами г0 и го2 зубчатых колес. Угол зацепления а ( угол между линией зацепления и нормалью к линии Oi O2 центров колес) постоянен. Делительная окружность разбивает высоту зуба ка головку и ножку.
 

Эвольвентное зацепление имеет ряд преимуществ перед циклоидальным, и до последнего времени оно в общем машиностроении имело исключительное распространение. Лишь в последнее время эвольвентному зацеплению приходится в ряде случаев сдавать свои позиции.
 

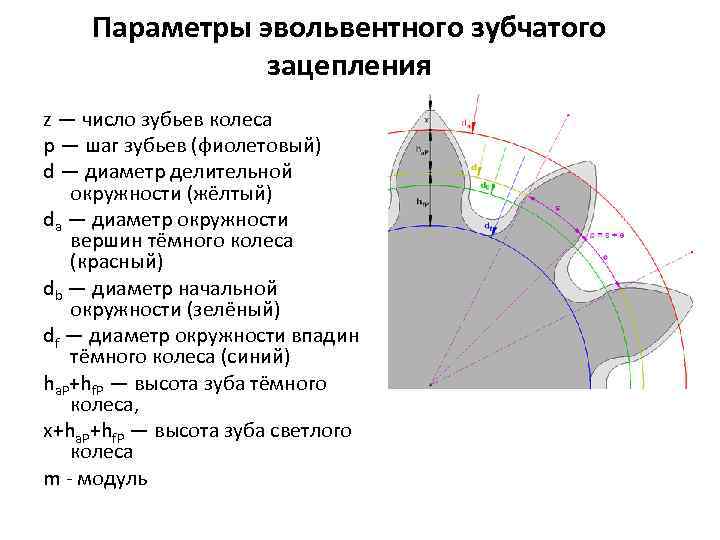
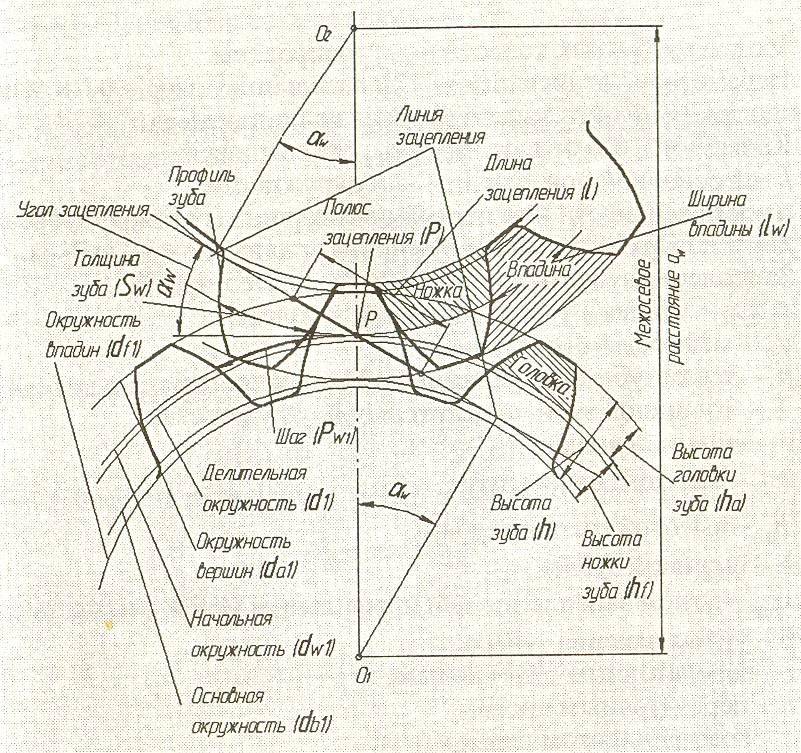
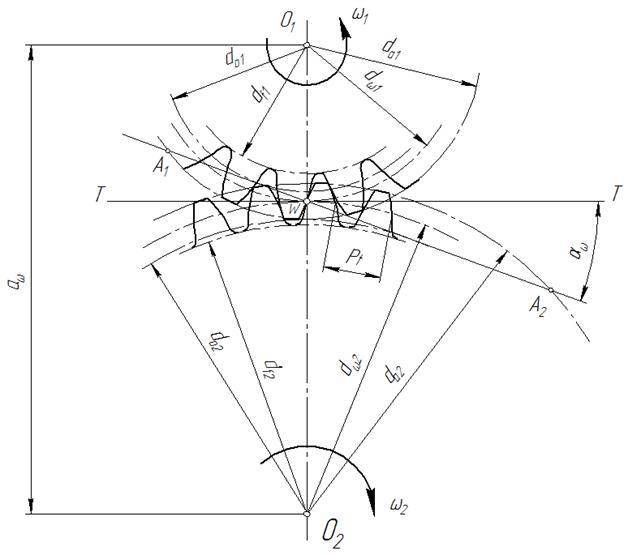
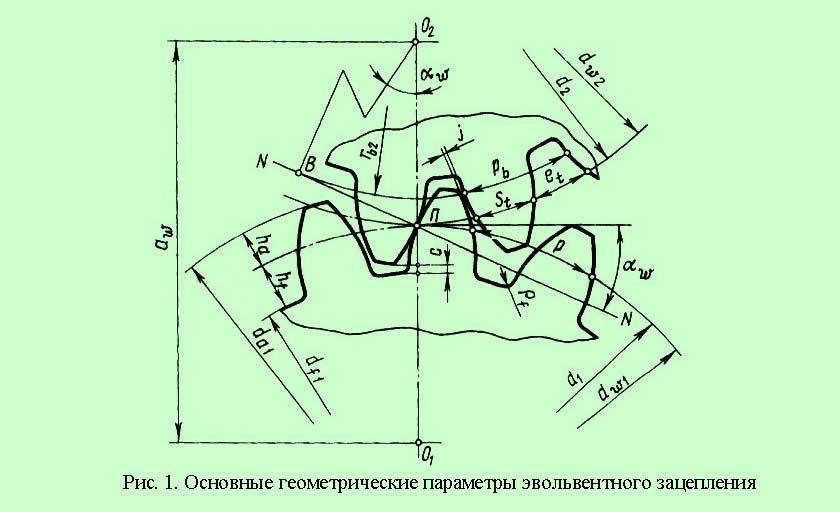
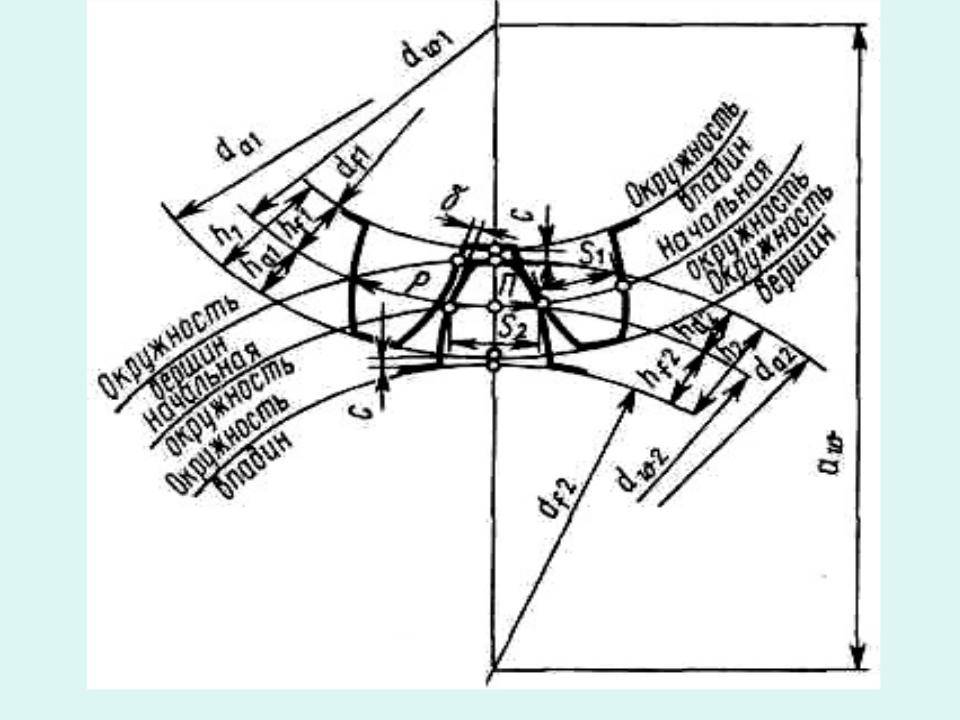
Эвольвентное зацепление колес характеризуется следующими основными элементами и параметрами.
 

Эвольвентное зацепление колес характеризуется следующими основными элементами и параметрами.
 

Эвольвентному зацеплению предшествовало циклоидальное. Часовое зацепление, являющееся разновидностью циклоидального зацепления, до сих пор применяется в часовой промышленности и вряд ли в этой отрасли приборостроения будет вытеснено эвольвентным зацеплением. В машиностроении циклоидальное зацепление применяется в винтовых насосах и компрессорах.
 

Почему эвольвентное зацепление является наиболее распространенным.
 

Почему эвольвентное зацепление имеет преимущественное применение.
 

Почему эвольвентное зацепление является наиболее распространенным.
 

Зубчатые передачи

Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут из­готавливаться на одном оборудовании, не­зависимо от количества зубьев и размеров головки.

Модули зацепления цилиндрических и ко­нических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных пе­редач по DIN 780; модули шлицевых соедине­ний по DIN 5480; модули зубчатого зацепле­ния нормального профиля для шестерен со спиральными зубьями по DIN 780.

Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; чер­вячных передач — DIN 3975; шлицевых соеди­нений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).

Форма зубьев гипоидных передач регла­ментируется стандартом DIN 867. В допол­нение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы заце­пления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.

Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (из­менение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подреза­ния у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.

Зубчатые передачи с точно заданным межосевым расстоянием

У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса произво­дится на одинаковую величину, но в противо­положных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.

Зубчатые передачи с изменяемым межосевым расстоянием

Изменение высоты головки зуба для ше­стерни и зубчатого колеса производится независимо друг от друга, поэтому межосе­вое расстояние передачи может изменяться. Допускаемые отклонения линейных разме­ров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.

Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры за­цепления без зазора между зубьями. Для определения зазора между зубьями допу­скаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в за­висимости от требуемой степени точности зубчатой передачи.

Следует отметить, что не обязательно стремиться к нулевому за­зору между зубьями. Для компенсации имею­щихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.

Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.

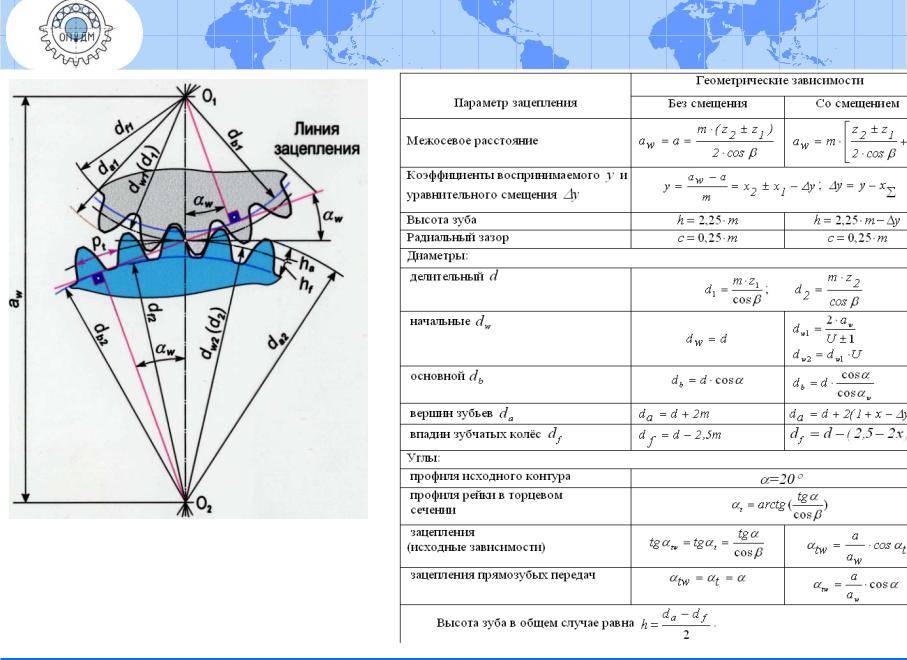
Геометрические параметры

Построенные проекта будущего колеса начинается с расчета его параметров.

Рассмотрим параметры эвольвентного зацепления:

• шаг;
• модуль;
• число зубьев;
• угол профиля;
• коэффициент смещения.

Шаг бывает двух видов:

1. Окружной — длина между равнорасположенных точек на соседних зубьях.
2. Угловой – центральный угол, характеризрующий дугу делительной окружности.

Модуль — диаметр круга шестерни в миллиметрах, измеряемый к одному зубу. Делится на три вида: начальный (показатель окружности колеса начальной поверхности), основной и делительный (окружность колеса со стандартными значениями модуля и шага).

Число зубьев может быть разное, и зависит от диаметра шестерни, технических параметров и свойств готового механизма. К их параметрам можно отнести:

• толщина зуба;
• ширина впадины;

Угол профиля определяется между определенной точкой зуба, которая лежит на делительной окружности шестерни и вектором, прочерченным к точке от центра круга.

Подобное сцепление используется в различных сферах. Его легко встретить в машиностроении (в коробках передач автомобилей, в строительной, военной, сельскохозяйственной технике, судостроении, гидронасосах, лебедках и часовых механизмах).

На сегодняшний день можно найти множество разновидностей подобных шестерен, которые имеют различные свойства и геометрию

При выборе зубчатых колес в первую очередь нужно обращать внимание на прочность и шумовые характеристики

Особого внимания требует твердость метала, что особо важно для нормальной работы соответствующего механизма

Выбор оборудования и инструмента

Нарезка выполняется на станках:

• фрезерных;
• строгальных;
• долбежных;
• токарных;
• протяжных.

Затем детали подвергают шлифовке на шлифовальных станках.

В мелкосерийном и единичном производстве очень часто нарезание шлицев осуществляется на шлицефрезерном или зубофрезерном оборудовании с использованием червячной фрезы и метода обкатки. Использование такого инструмента эффективно как для прямобочных, так и для эвольвентных шлицев.

Горизонтально-фрезерный станок для нарезания шлицев используется в паре с фасонной дисковой фрезой. Для одновременной нарезки нескольких пазов используют делительную головку. Стоит отметить, что для изготовления шлицов такой способ используют крайне редко из-за неточностей по шагу и ширине. Целесообразно будет провести на горизонтально-фрезерном станке с дисковой фрезой черновую обработку детали, оставив припуск на чистовую обработку и шлифовку. Чистовую обработку пазов проводят специальными торцевыми фрезами, а для треугольного шлицевого соединения применяют треугольные фрезы.

Используется метод обкатки с применением долбяка. За высокое качество, получаемых поверхностей зубодолбежное оборудование используются в массовом производстве.

Помимо долбежных станков, широкое распространение в массовом и крупносерийном производстве шлицевых соединений получили строгальные и протяжные станки. Такое оборудование в несколько раз эффективнее и производительнее фрезерных станков. Нарезка строганием осуществляется с применением набора резцов, количество и размеры которых зависят от числа зубьев, ширины и глубины пазов соединения. При протягивании используют инструмент под названием протяжка. Этот инструмент имеет несколько режущих зубьев разной высоты, которые при поступательном движении срезать часть металла с заготовки.

Для изготовления эвольвентных соединений применяют холодную накатку с использованием специальных роликовых головок. Таким инструментом изготавливают изделия с большим количеством зубьев. По своей эффективности метод холодной накатки выше фрезерования в 10 раз.

После нарезки зубьев и термической обработки, все изделия подвергают шлифовке. Это позволяет добиться требуемой шероховатости и избежать зацепления сопрягаемых деталей в работе. Для шлифования используют следующий инструмент:

• фасонный круг;
• дисковый круг;
• конический круг.

Для шлифования внутренних поверхностей в некоторых случаях применяют оправку.

Геометрический расчет элементов цилиндрической зубчатой передачи

Исходные данные для расчета:

• Модуль m = 4 мм;
• Число зубьев шестерни Z1 = 18;
• Число зубьев колеса Z2 = 30;
• Диаметр вала (ведущий) DB1 = 22 мм;
• Тип шпонки – Призматическая;
• Число шлицев Z – 8;
• Внутренний диаметр шлицев d = 22 мм;
• Диаметр вала (ведомый) DB2 = 30 мм;
• Ширина шлица b = 6 мм;
• Тип – D.

Результаты геометрического расчета цилиндрической зубчатой передачи

• Делительный диаметр шестерни d1=mz1=4×18=72 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Высота головки зуба ha=m =4 мм;
• Высота ножки зуба hf=1,25m=1,25×4=5 мм;
• Высота зуба h=ha+hf=2,25m=2,25×4=9 мм;
• Диаметр вершин зубьев шестерни da1=d1+2ha1=72+2×4=80 мм;
• Диаметр впадин шестерни df1=d1-2hf=72-2×5=62 мм;
• Длина ступицы шестерни Lст1=1,5DB1=1,5×22=33 мм;
• Наружный диаметр ступицы шестерни Dст1=1,6DB1=1,6×22=35,2 мм;
• Диаметр вала шестерни D1=1,2×22=26,4 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Диаметр вершин зубьев колеса da2=d2+2ha=120+2×4=128 мм;
• Диаметр впадин колеса df2=d2-2hf2=120-2×5=110 мм;
• Длина ступицы колеса Lст2=1,5DB2=1,5×30=45 мм;
• Наружный диаметр ступицы колеса Dст2=1,6DB2=1,6×30=48 мм;
• Диаметр вала колеса D2=1,2DB2=1,2×30=36 мм;
• Ширина зубчатого венца b=6m=6×4=24 мм;
• Толщина обода зубчатого венца δ1=2,25m=2,25×4=9 мм;
• Толщина диска δ2=1/3b=8 мм;
• Межосевое расстояние a=0,5(d1+d2)=0,5(72+120)=96 мм;
• Длина шлицев Lшл=(1,5. 2)Lст2=(1,5. 2)45=72 мм.

Обозначение шлицевых эвольвентных соединений

Варианты условных обозначений эвольвентных шли­цевых соединений на чертежах показаны на рис 17.

Центрирование по боковым сторонам

Рисунок 17. Шлицевое эвольвентное соединение при центрировании по боковым сторонам зубьев.

Шлицевое эвольвентное соединение с D = 65мм; т = 3 мм, при центрировании по боковым сторонам зубьев с посадкой 9H/9g.

Центрирование по наружному диаметру:

Центрирование по внутреннему диаметру:

здесь: D=65, m=3, центрирование по внутреннему диаметру с посадкой H7/g6, посадки остальных поверхностей предусмотрены в табл.5.

Предельные значения радиального биения должны соответствовать значениям табл…., а ориентировочно это половина суммарного допуска

T ( т.е. Fr = 0,5 T ).

Пример выбора параметров эвольвентного шлицевого соединения.

Для подвижного шлицевого соединения D = 50 мм, с модулем т = 2 мм, без повышенных требований к соосности, выбрать геометрические параметры, определить предельные размеры вала и втулки, представить схему расположения полей допусков с оценкой предельных зазоров.

Принимаем центрирование шлицевого соединения по боковым поверхностям зубьев. По номинальному (исходному) диаметру соединения D = 50 мм и модулю т = 2 мм, по табл. 2 определяем число зубьев z = 24.

• Геометрические параметры получаем в соответствии с табл. 1,
• где:
• для вала толщина зуба по делительной окружности
• s =(π/2) m+2 Xm tgα,
• здесь смещение исходного контура будет:

Xm=0.5(D — m z -1.1 m)

Xm=0.5 · (50 — 2·24 -1.1·2) = -0,1мм

1. Теперь:
2. s =(3,1415/2) · 2+2· (-0,1) · 0,5773
3. s =3,1415+(-0,11547)=3,026мм
4. для шлицевой втулки ширина впадины по делительной окружно­сти
5. s=e=3,026мм
6. диаметр окружности вершин зубьев:
7. da =d-0,2m
8. da =50-0,2·2=49,6 мм.
9. диаметр окружности вершин зубьев втулки
10. Da = D – 2m
11. Da = 50 – 2·2 = 46мм.
12. Диаметр делительной окружности вычисляем
13. d = mz = 2·24 =48мм.

Принимаем плоскую форму дна впадины и согласно примечанию к табл. 4. определяем, диаметр окружности впадин вала

• df тах = D­- 2,2т = 50 — 2,2·2 = 45,6 мм
• Диаметр окружности впадины втулки будет
• Df = D = 50 мм.

Учитывая заказанную подвижность соединения выбираем посадки с зазорами. на каждый размер шлицевых деталей по табл.4.

Для центрирования по боковым сторонам предусмотрены предпочтительные посадки 9H/9h и 9H/9g,больший зазор у 9H/9g, её принимаем и получаем формулу соединения.

По таблице приложения 22 выписываем параметры, для шлицевой втулки c полем 9H при D = 50 мм, и модуля т = 2 мм, ES=+71, ESe=+26, EI=0, для шлицевого вала c с полем 9g: es=-11, ese=-37, ei=-82.

Для большего диаметра примем посадку H16/d9 по таблице 4. Параметры шлицевой втулки по Df=50 ,будут определены по таблицам приложения: EI=0, ES=+1600, шлицевого вала по da= 49,6,es=-80,ei=-142.

Для меньшего диаметра по табл. 4 принимаем посадку H11/h16 определяя характеристики по таблицам допусков и посадок, приложения. Параметры шлицевой втулки при Da=46, будут EI=0, ES=+160, шлицевого вала при df= 45,6, es=0, ei=-1600мкм,

По полученным значениям отклонений не трудно получить предельные размеры поверхностей соединения. Результаты удобно представить в виде таблицы табл.6. Подсчитываем предельные размеры и допуски, занося в таблицу.

Таблица 6. Результаты.

Параметр мм	Поле допуска	Предельные отклонения мкм	Предельные размеры мм	Допуск мм
ES (es)	ESe (ese)	EI (ei)	max	min
Шлицевый вал
s=3,026	9g	-11	-37	-82	2,989	2,944	0.045
da=49,6	d9	-80	—	-142	49,520	49,458	0,062
df=45,6	h16	—	-1600	45,6	44,0	1,6
Шлицевая втулка
e=3,026	9H	+71	+26	3,097	3,052	0,045
Df=50	H16	+1600	—	51,6	50,0	1,6
Da=46	H11	+160	—	46,16	46,0	0,16

Схемы расположения полей допусков изображены на рис.9.

1. Рисунок 18. Графическое представление посадок шлицевого соединения 65x3x 9H/9g Гост 6033-60
2. Определяем наибольший Smax и наименьший Smin зазоры для посадки 9H/9g по боковым поверхностям зубьев:
3. Smax =eimax — Smin = 3,097 — 2,944 = 0,153мм;
4. Smin =eimin — Smax = 3,052 — 2,989 =0,063 мм.