Линейчатые поверхности

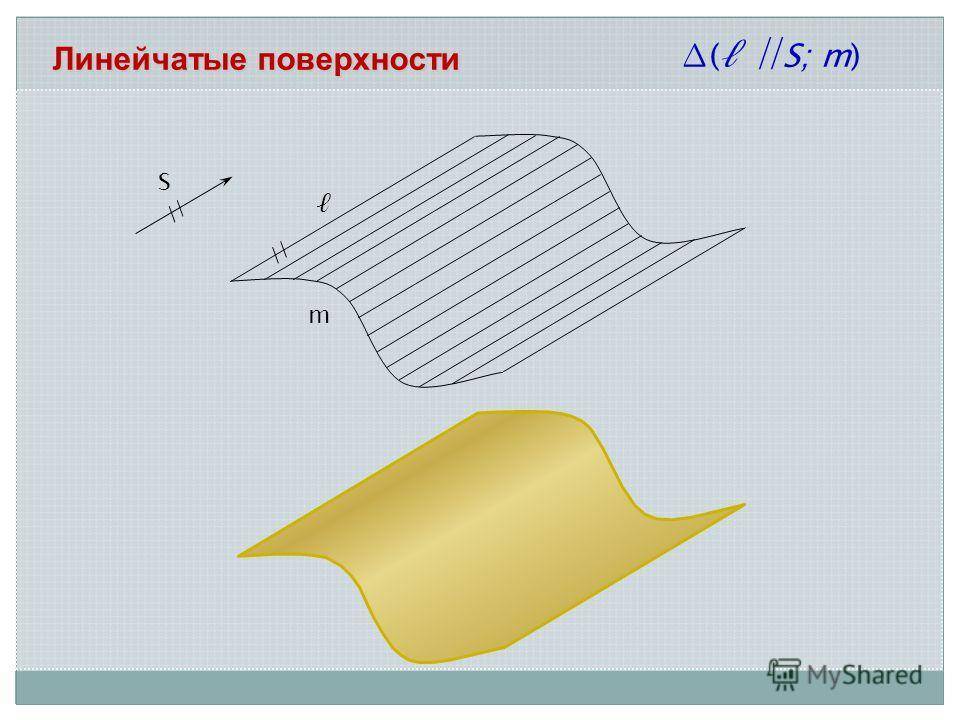
Определение и параметрическое представление

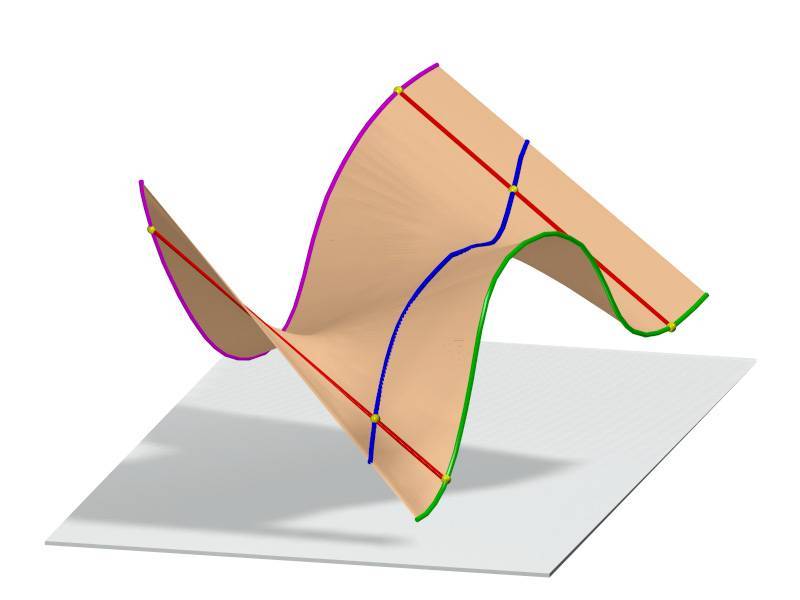
Линейчатая поверхность, образованная двумя кривыми Безье как направляющими (красный, зеленый)

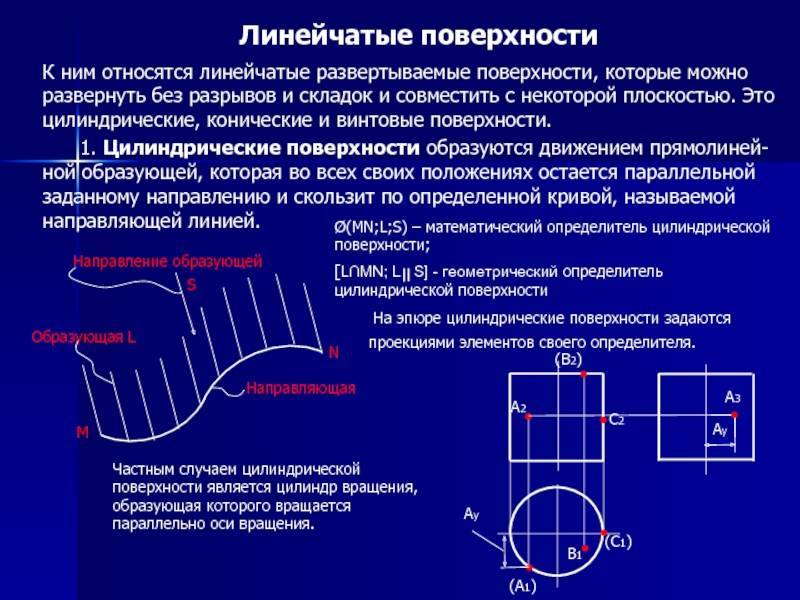
Двумерный называется линейчатая поверхность, если это однопараметрического семейства линий. Линии этого семейства являются генераторы линейчатой ​​поверхности.

Линейчатая поверхность может быть описана параметрическое представление формы

(CR) Икс(ты,v)=c(ты)+vр(ты) , v∈р ,{ displaystyle quad mathbf {x} (u, v) = { color {красный} mathbf {c} (u)} + v ; { color {blue} mathbf {r} (u)} , v in mathbb {R} ,}.

Любая кривая v↦Икс(ты,v){ Displaystyle ; v mapsto mathbf {x} (u_ {0}, v) ;} с фиксированным параметром ты=ты{ displaystyle u = u_ {0}} образующая (линия) и кривая ты↦c(ты){ Displaystyle ; и mapsto mathbf {c} (и) ;} это директриса представительства. Векторы р(ты)≠{ Displaystyle ; mathbf {r} (и) neq { bf {0 ;}}} Опишите направления генераторов.

Директриса может свернуться в точку (в случае конуса см. Пример ниже).

В качестве альтернативы линейчатая поверхность (CR) можно описать

(CD) Икс(ты,v)=(1−v)c(ты)+vd(ты) { displaystyle quad mathbf {x} (u, v) = (1-v) ; { color {красный} mathbf {c} (u)} + v ; { color {зеленый} mathbf {d} (u)} }

со второй директрисой d(ты)=c(ты)+р(ты){ Displaystyle ; mathbf {d} (u) = mathbf {c} (u) + mathbf {r} (u) ;}.

Как вариант, можно начать с двух непересекающихся кривых. c(ты),d(ты){ Displaystyle mathbf {с} (и), mathbf {d} (и)} в качестве директрис и обойтись (CD) линейчатая поверхность с направлением линий р(ты)=d(ты)−c(ты) .{ Displaystyle ; mathbf {r} (u) = mathbf {d} (u) – mathbf {c} (u) .}

Для создания линейчатой ​​поверхности двумя направляющими (или одной направляющей и векторами направлений линий) важна не только геометрическая форма этих кривых, но и их специальные параметрические представления влияют на форму линейчатой ​​поверхности (см. Примеры ), г)).

Для представления теоретических исследований (CR) более выгодно, потому что параметр v{ displaystyle v} появляется только один раз.

Применение и история разворачивающихся поверхностей [ править ]

Развивающееся соединение двух эллипсов и его развитие

Детерминантное условие для развертывающихся поверхностей используется для определения численно складываемых связей между пространственными кривыми (директрисами). На схеме показана развивающаяся связь между двумя эллипсами, находящимися в разных плоскостях (одна горизонтальная, другая вертикальная), и ее развитие.

Впечатление об использовании развертываемых поверхностей в автоматизированном проектировании ( САПР ) дается в документе « Интерактивное проектирование развертываемых поверхностей»

Историческое исследование по развёртывающимся можно найти в развертывающейся поверхности: их история и применение

7.6. Сферическая поверхность

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

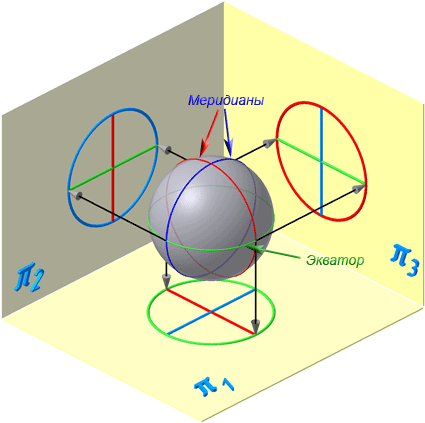Рисунок 7.10 – Проецирование сферической поверхности

Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.

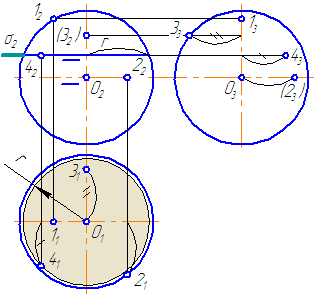Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек

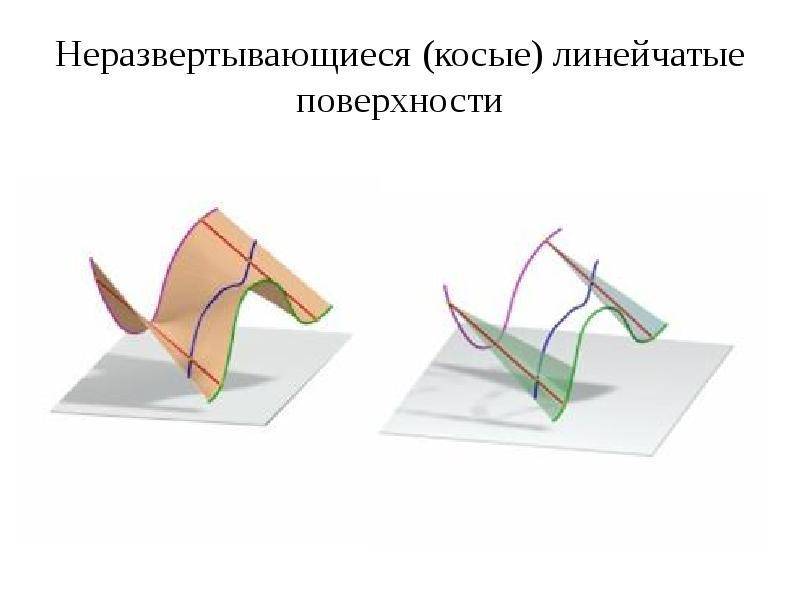
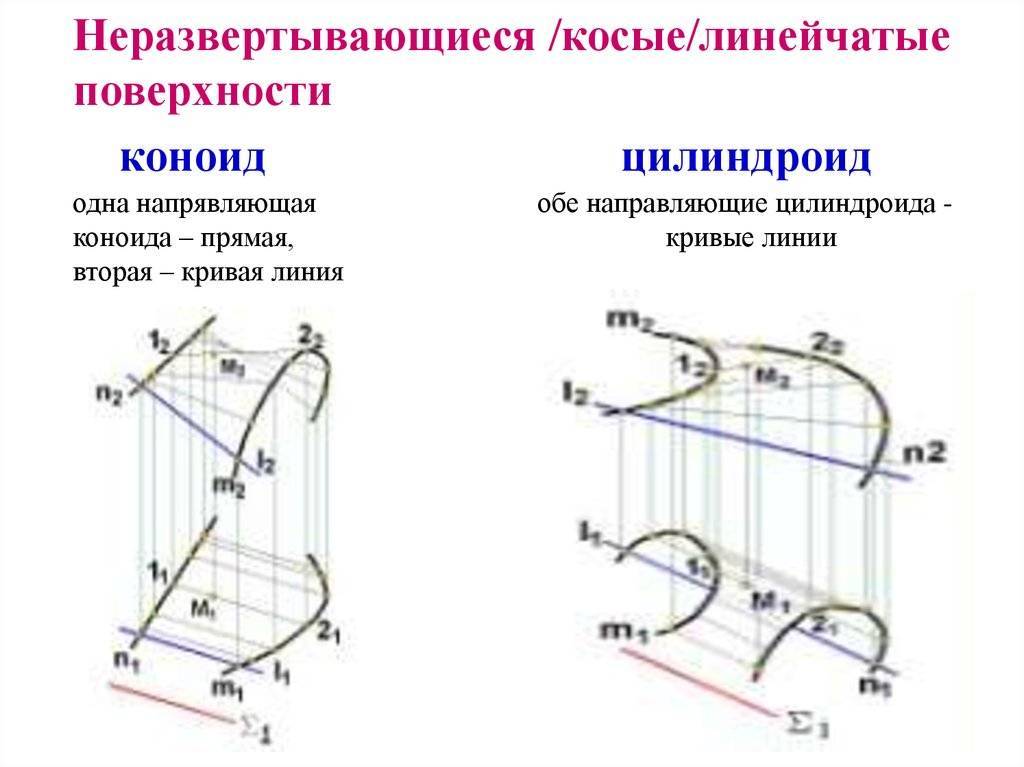
Неразвертывающиеся или косые поверхности

Их возникновение часто обусловлено передвижением прямолинейной образующей вдоль траектории, сформированной тремя направляющими. Они конкретно определяют закон перемещения и бывают прямыми или кривыми. Есть частные случаи, когда траектория движения определяется:

• двумя направляющими и произвольной плоскостью;
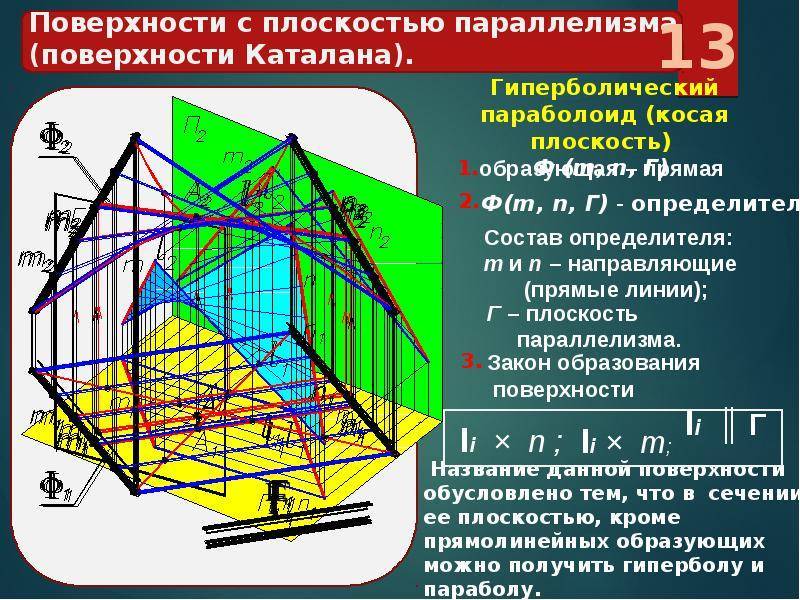
• направляющими произвольной формы и плоскостью параллелизма (например, область проекции).

Направляющая плоскость замещает одну из линий траектории. С ней движущаяся прямая составляет постоянный угол.

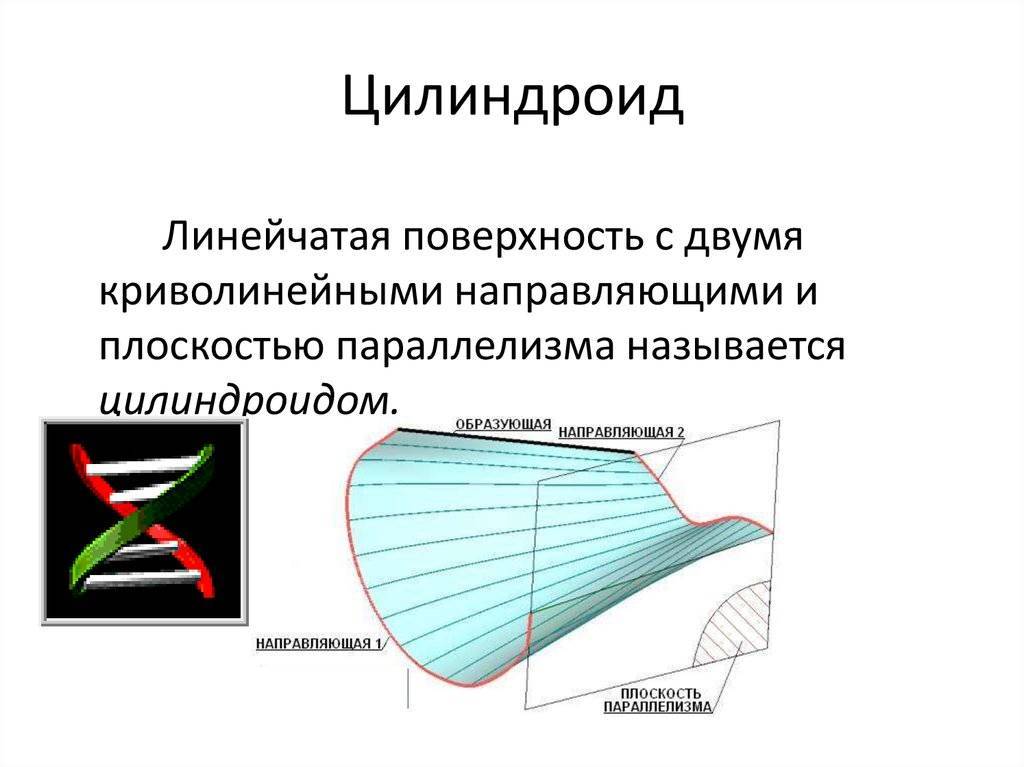
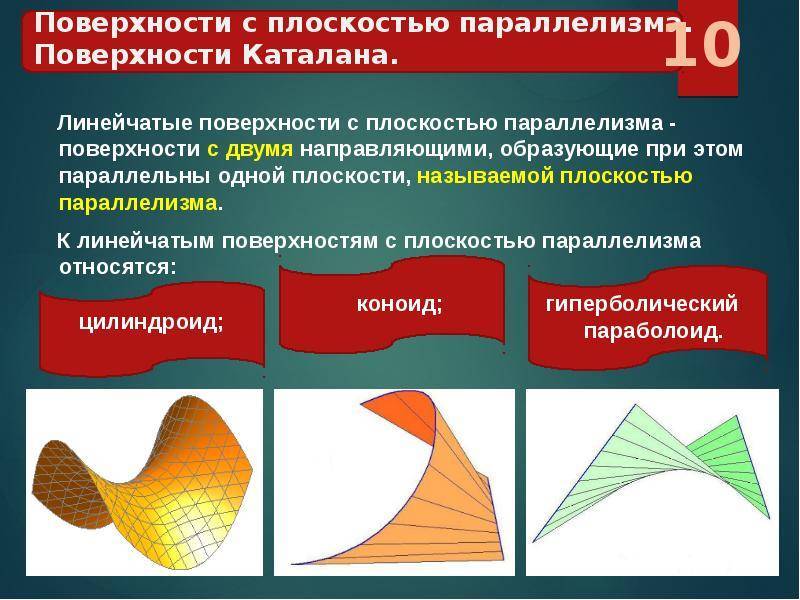
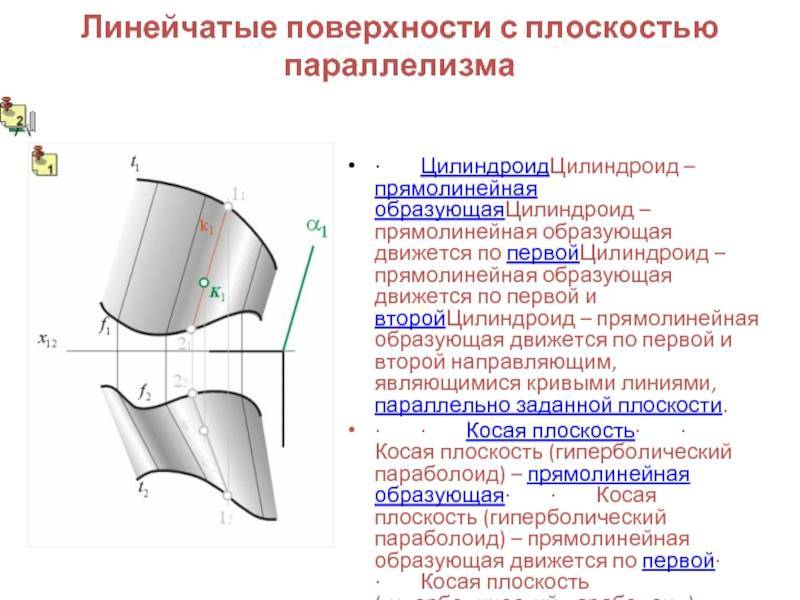
Примеры таких объектов: цилиндроид, коноид, гиперболический параболоид. Их основные характеристики приведены в таблице.

Вид	Определители (наряду с плоскостью параллелизма)	Характеристика	Некоторые области применения
Цилиндроид	2 кривые направляющие	Изобразить образующие на комплексных чертежах можно так: 1.Параллельно параллелизму провести серию плоскостей. 2.Определить точки, в которых кривые направляющие цилиндроида пересекаются с плоскостями. Если за параллелизм принять одну из плоскостей уровня, что облегчает построение, то линии будут соответствовать линиям уровня.	Проектирование габаритных, большого диаметра, воздуховодов
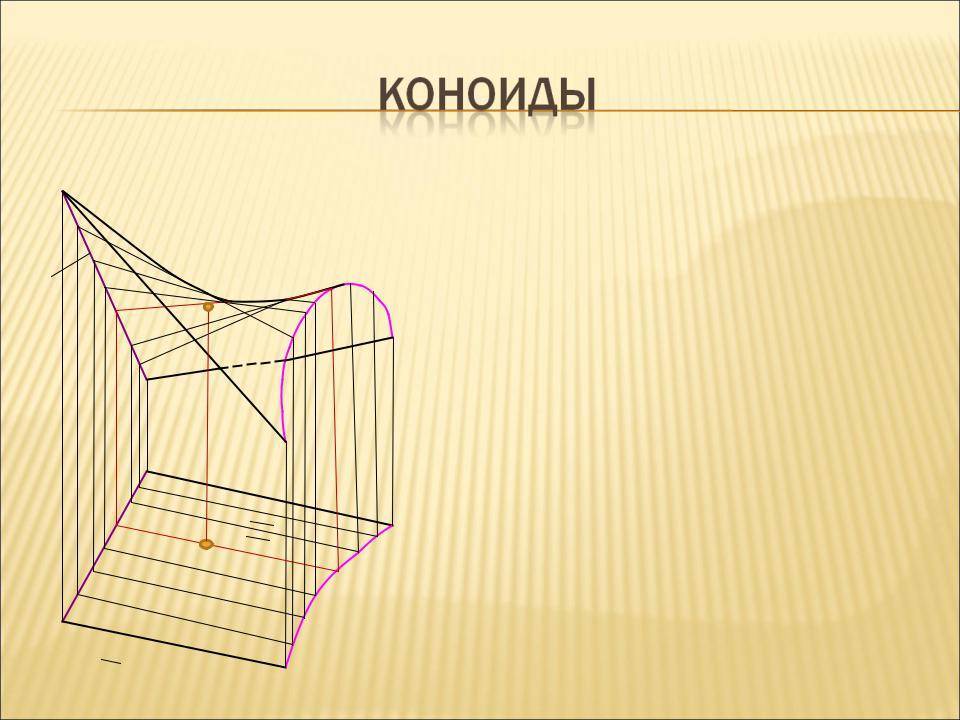
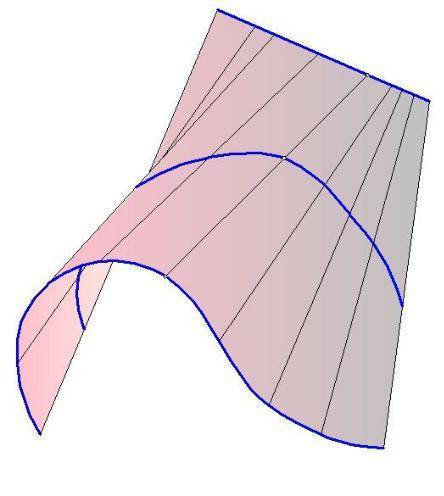
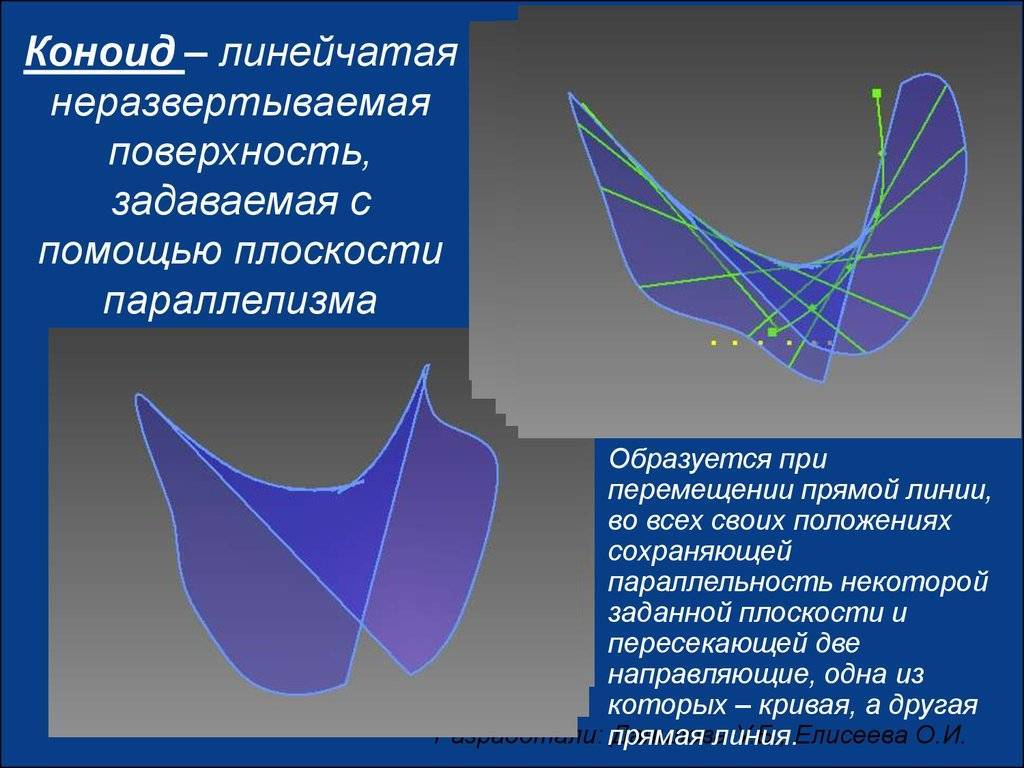
Коноид	2 направляющие: · прямолинейная	1. Особый случай цилиндроида. 2. Прямой коноид имеет направляющую прямолинейную, расположенную под прямым углом к области параллелизма.	Гидротехническое строительство, при конструировании опор мостов
Параболоид гиперболический (синонимично понятию косой плоскости)	2 пересекающиеся прямые направляющие	1. Изображается как несколько прямых согласно закону: образующая должна пересекать направляющие и проходить параллельно установленной области параллелизма. 2. При пересечении определенными плоскостями в сечениях получаются гиперболы и параболы.	При разработке конструкций гидротехнических сооружений, дорог, откосов, шлюзов, каналов, крыльев ветряков

Линейчатые поверхности представляют собой математические абстракции, благодаря которым можно получить представление о свойствах предметов.

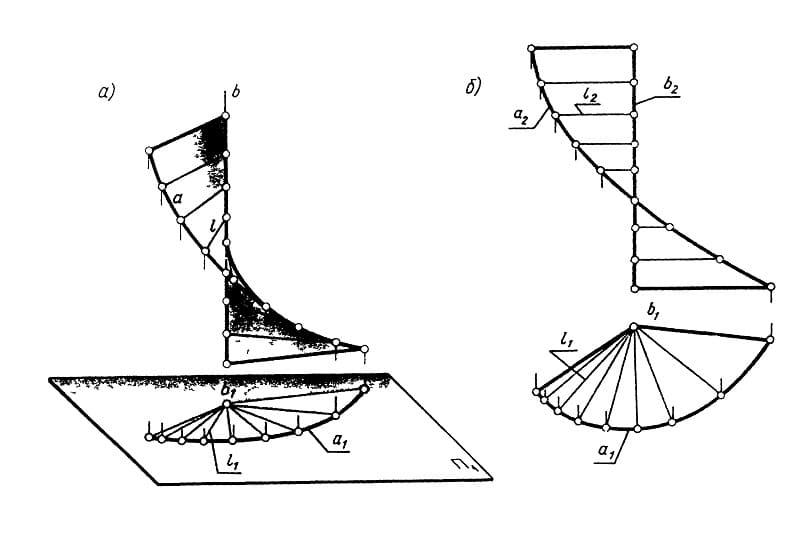
Их моделирование, математическое, геометрическое описание позволяют проектировать различные тела и конструкции в машиностроении, архитектуре. Современные программы компьютерного проектирования, например КОМПАС 3D, облегчают и автоматизируют процесс моделирования таких объектов.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

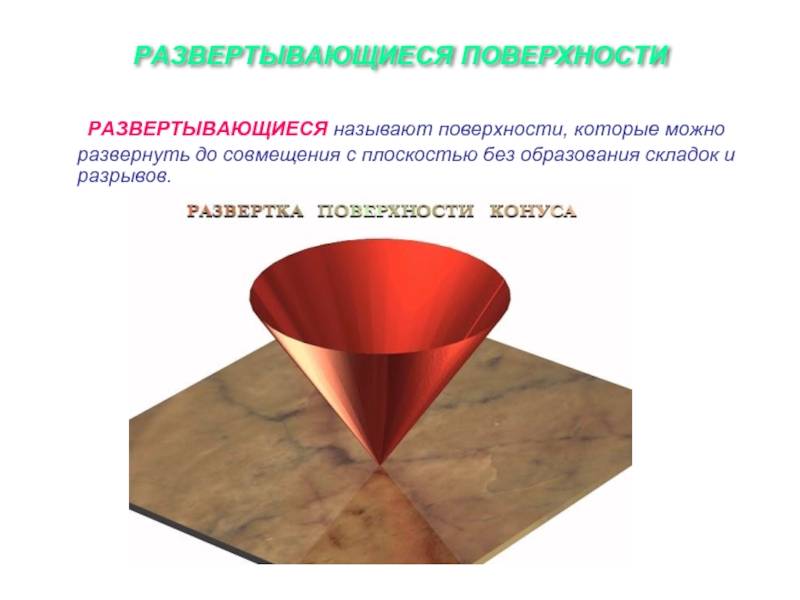
Развертывающиеся поверхности

Эти объекты важны для листопрокатного производства, текстильной промышленности, авиа- и автомобилестроения. Представление о них основывается на допущении, что они обладают гибкостью, но они нерастяжимы и несжимаемы. Под развертывающимися понимают области, которые, изгибая, можно совмещать с плоскостью без порывов, перегибов и складок. Таким образом получается развертка. Это свойство характерно для многогранных объектов и объектов, которые имеют ребра возврата.

Ребро возврата – это направляющая кривая в пространстве, которую касается прямая при передвижении. В системе отсчета развертывающаяся линейчатая поверхность определяется ребром возврата. Указанными характеристиками обладают: торс, а также его частные случаи: объекты, имеющие форму конуса, цилиндра, призмы, пирамиды.

Торс

Торсы используются при проектировании деталей и узлов в машиностроении. Образование линейчатых поверхностей, имеющих вид торса, происходит при передвижении образующей, которая во всех позициях проходит по касательной относительно ребра возврата. Оно, совместно с движущейся прямой, определяет торс в пространстве. Этот геометрический объект составляют две полости, граничащие по ребру возврата.

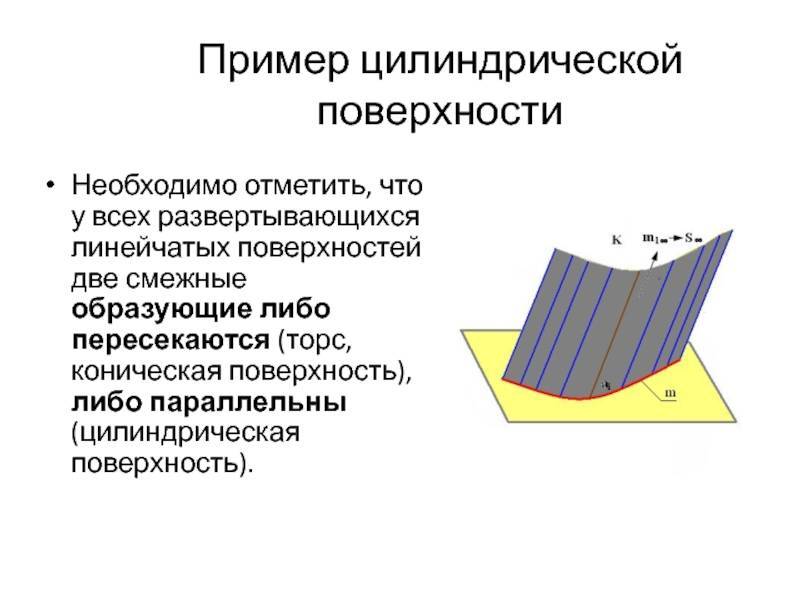
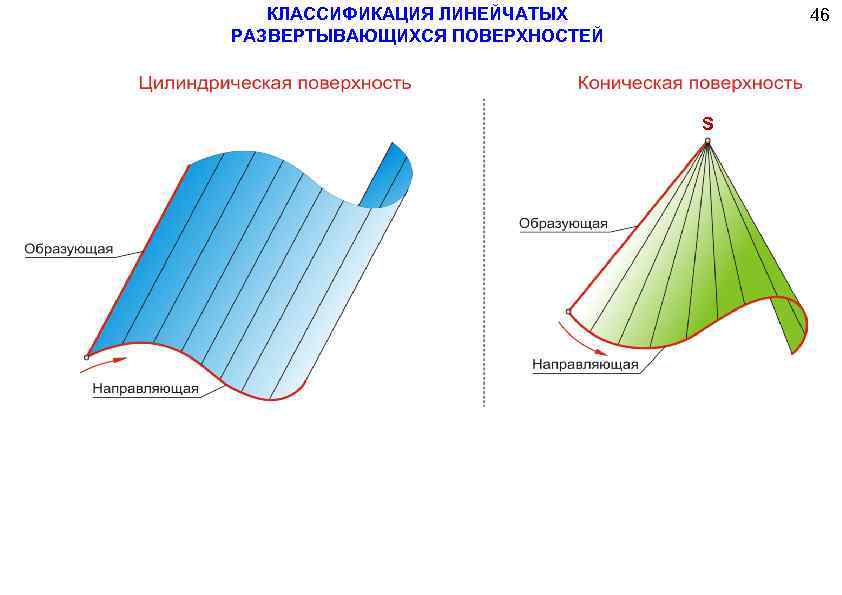
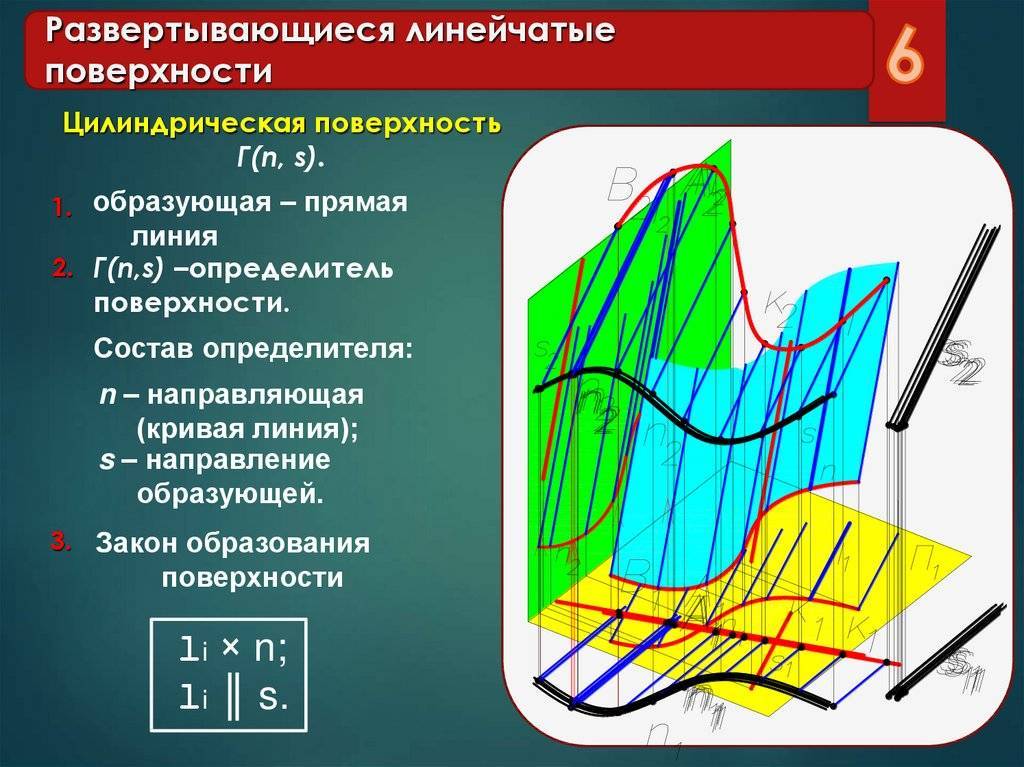
Цилиндрическая

Это особый вид торса. При этом ребро возврата переродилось в несобственную точку, удаленную на бесконечное расстояние. Построенная прямая образующая движется параллельно самой себе по установленной кривой. Чтобы определить цилиндрическую поверхность надо задаться: вектором перемещения и криволинейной траекторией движения.

Коническая

В ней ребро возврата преобразовалось в собственную точку, через которую, по определенной кривой, проходит образующая. Эта точка служит вершиной конуса. Такой объект может складываться из двух полостей. Для его определения задаются указанными точкой и кривой.

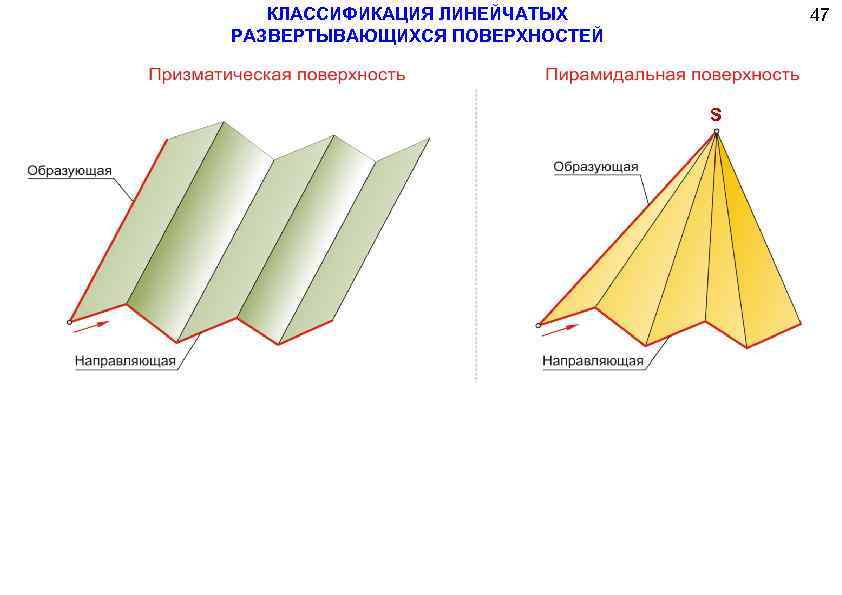
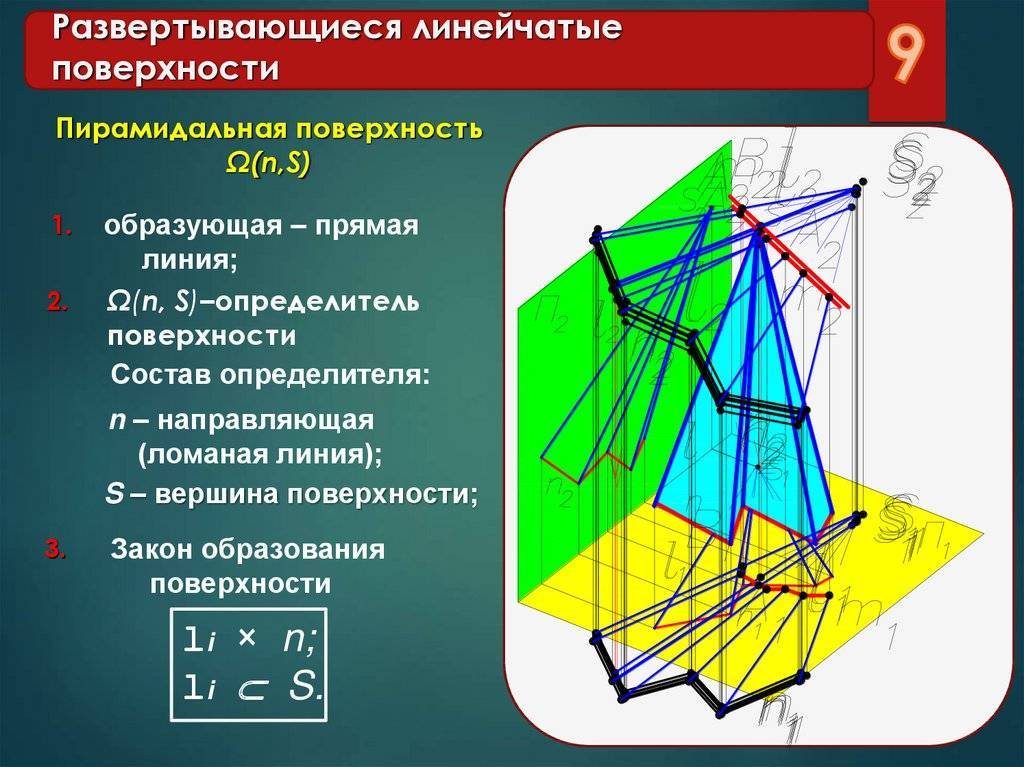
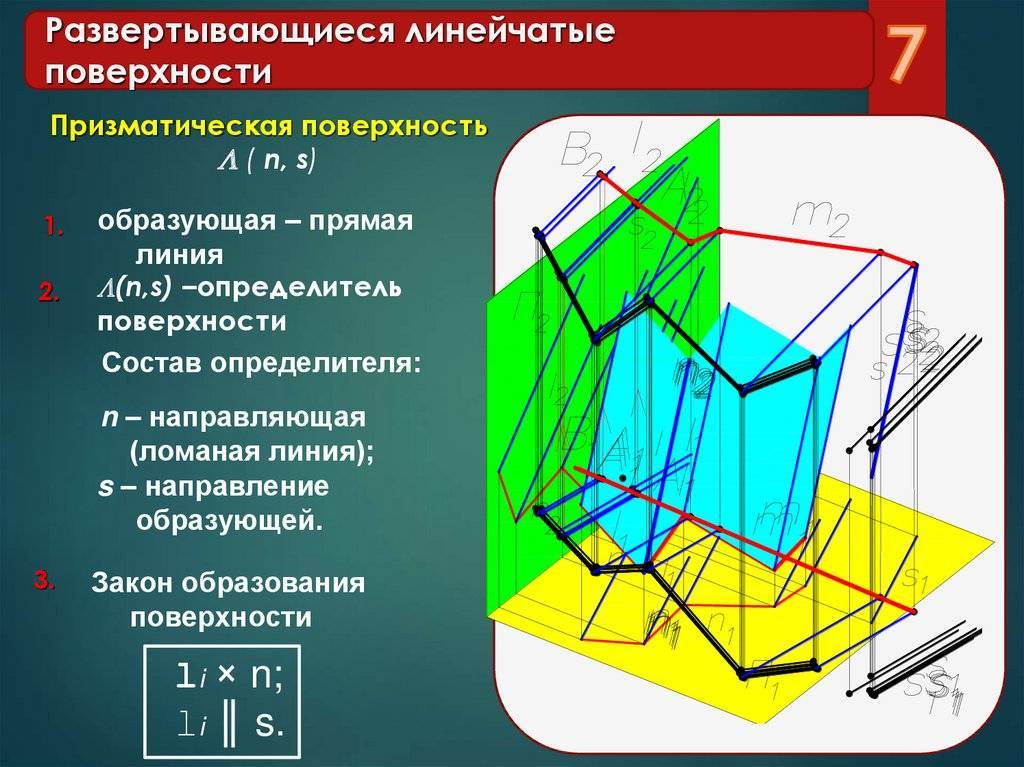
Призматическая и пирамидальная

Призматическая отличается от цилиндрической тем, что движение прямой происходит не по кривой траектории, а по ломанной. Ребро возврата преобразовалось в несобственную точку, которая находится на бесконечном расстоянии.

Пирамидальная и конусная различаются формой траектории движения прямой. У конусной — траектория движения криволинейная, у пирамидальной – ломанная.

У перечисленных видов две смежные прямые могут:

• пересекаться (торс, коническая, пирамидальная);
• быть параллельными (цилиндрическая, призматическая).

Чтобы получить уравнение поверхности развертывающейся надо решить систему двух уравнений:

1. уравнения образующей.
2. уравнения направляющей.

Рассмотренные объекты могут быть замкнутыми, если траектория имеет форму окружности или замкнутого многоугольника.

Параметрическое представление

Пример линейчатой ​​поверхности.

Мы можем описать линейчатую поверхность S , рассматривая его как в виде семейства линий D ( U ) в зависимости от параметра у обхода части I множества действительных чисел . Для этого достаточно , чтобы дать для каждого U в I точку P ( U ) и направляющий вектор из D ( ¯u ). Тогда мы получим параметрическое представление поверхности S  :
V(ты)→{\ displaystyle {\ overrightarrow {V (u)}}}м∈S⟺∃ты∈я∃v∈рM(ты,v)знак равноп(ты)+vV(ты)→.{\ Displaystyle м \ в S \ iff \ существует и \ в я \ четырехъядерный \ существует v \ в \ mathbb {R} \ четырехъядерный M (u, v) = P (u) + v \, {\ overrightarrow {V ( u)}}.}

Дуга установлено с помощью называется директрисой кривой из S .
ты∈я↦п(ты)∈р3{\ Displaystyle и \ ин I \ mapsto P (u) \ in \ mathbb {R} ^ {3}}

В примере напротив мы взяли
п(ты)знак равно(ты,-ты2,ты3)етV(ты)→знак равно(-ты2,1,ты).{\ Displaystyle P (u) = (u, -u ^ {2}, u ^ {3}) \ quad {\ rm {et}} \ quad {\ overrightarrow {V (u)}} = (- u ^ {2}, 1, u).}

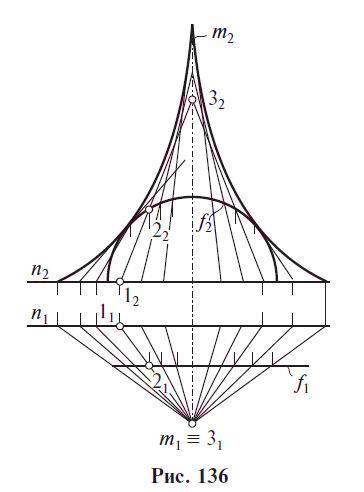
Линейчатые и нелинейчатые поверхности.

Линейчатые поверхности — поверхности, которые образуются с помощью прямой линии. Нелинейчатые поверхности — поверхности, которые образуются с помощью кривой линии. Развертывающиеся поверхности — поверхности, которые после разреза их по образующей могут быть совмещены с плоскостью без наличия разрывов и складок. Неразвертывающиеся поверхности — поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок. Поверхности с постоянной образующей — поверхности, образующая которых не изменяет своей формы в процессе образования поверхности. Поверхности с переменной образующей — поверхности, образующая которых изменяется в процессе образования поверхности.

Линейчатые развертываемые поверхности:

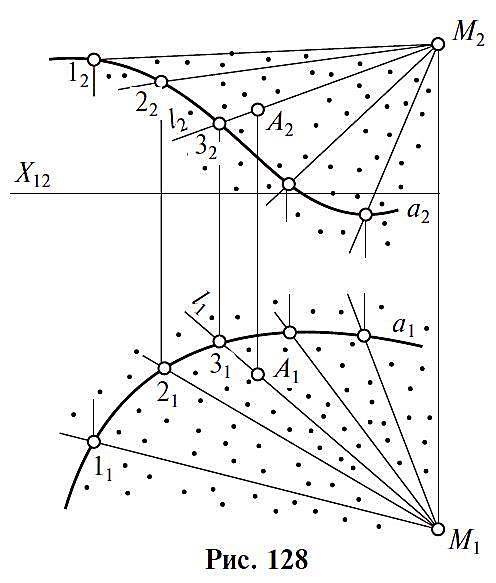
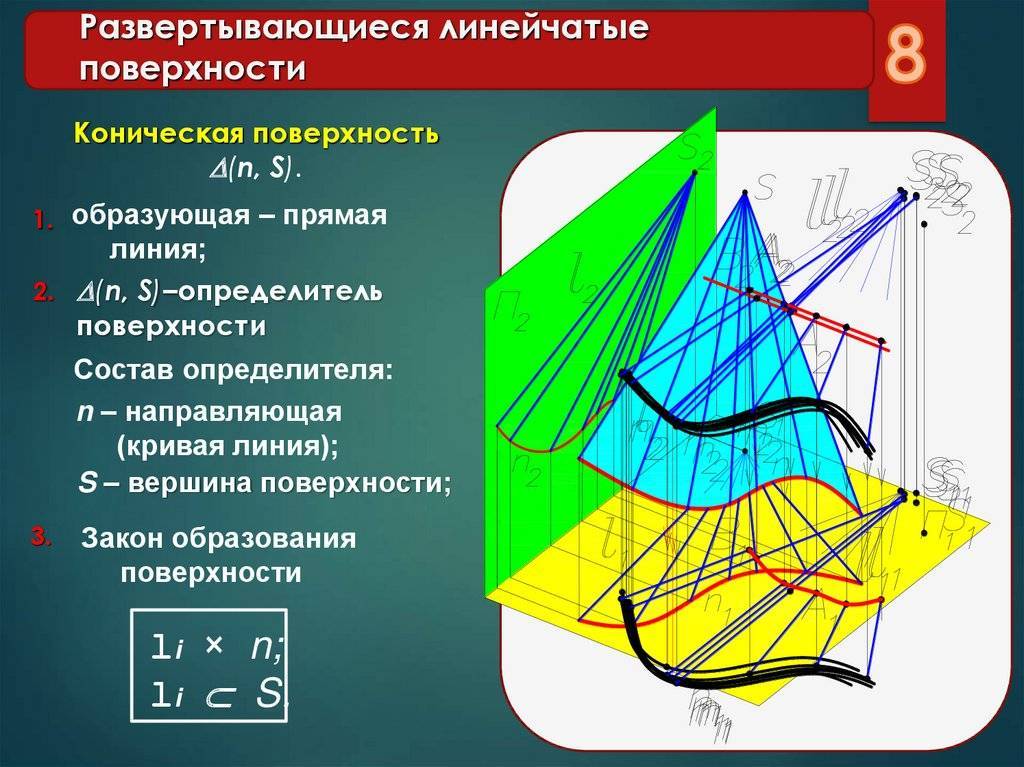
1. Конические поверхности задаются движением прямой линии l, проходящей через неподвижную точку М, по некоторой направляющей кривой линии а. (рис 128)

2. Цилиндрические поверхности задаются движением прямой, параллельной некоторому направлению, по заданной направляющей кривой. (рис 129)

3.

Поверхность с ребром возвратаа

Линейчатые неразвертываемые поверхности:

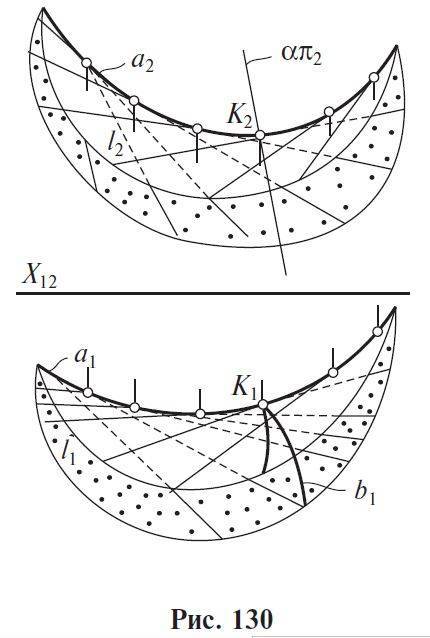
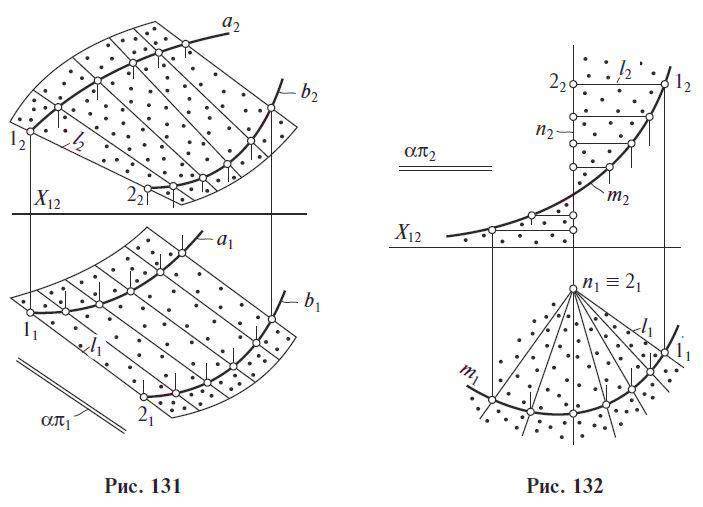
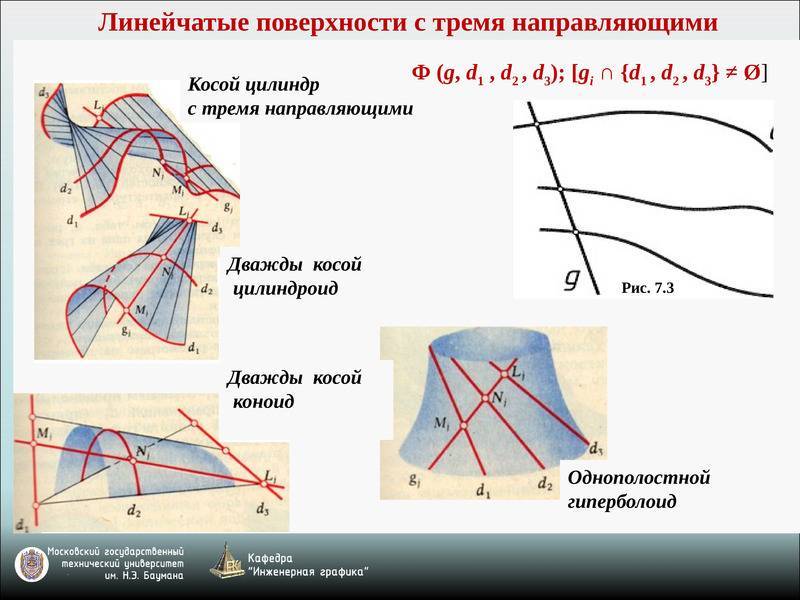
1) Цилиндроидобразован движением прямой, параллельной заданной плоскости параллелизма α, по двум пространственным кривым a и b.

2) Коноид образован движением прямой по одной прямолинейной направляющей n, по другой криволинейной направляющей m, оставаясь параллельной некоторой плоскости параллелизма α || π₁.

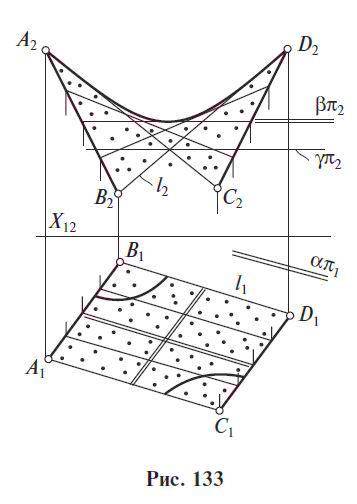
3) Гиперболический параболоид, или косая плоскость, задается двумя скрещивающимися прямыми направляющими АВ, CD и плоскостью параллелизма α(απ₁).

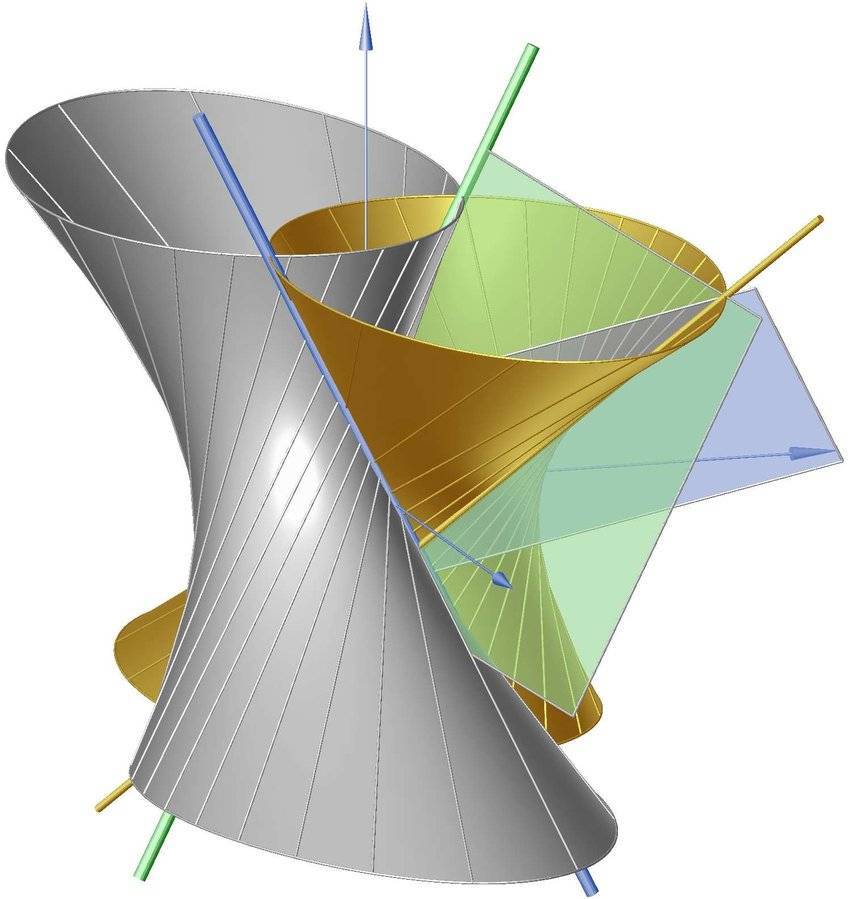
4) Однополостный гиперболоид образуется движением прямолинейной образующей l по трем прямолинейным скрещивающимся направляющим а, b, c.

5) Косой цилиндр с тремя направляющими образуется движением прямолинейной образующей по трем направляющим, одна из которых обязательно кривая.

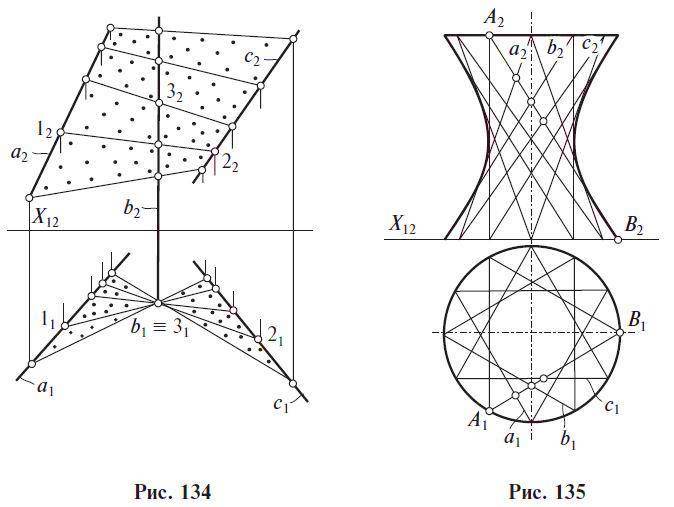
Нелинейчатые неразвертываемые поверхности:

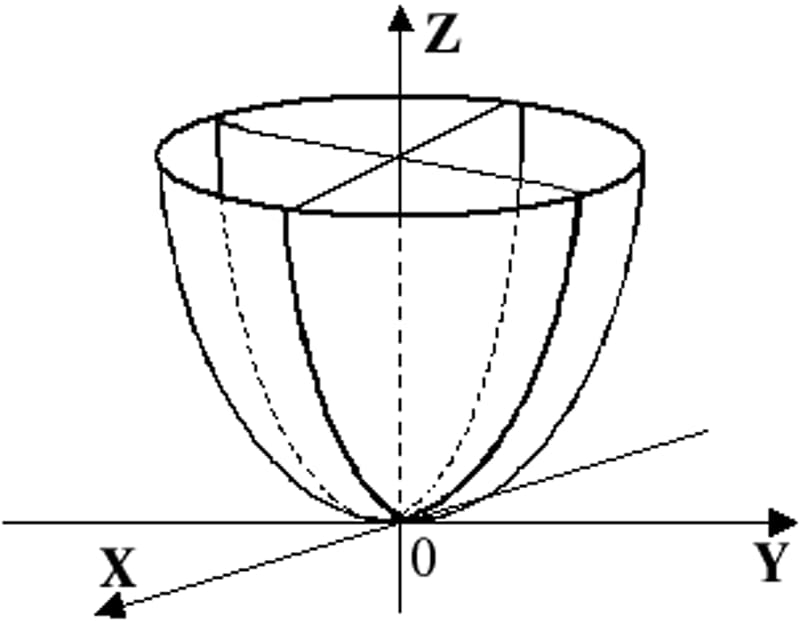
1) Эллипсоид трехосный образован движением переменного эллипса вдоль одной из трех его осей Х, Y, Z . Образующие эллипсы подобны.

2) Эллиптический параболоид образуется движением деформирующегося эллипса по двум направляющим параболам m и n

3) Двуполостный гиперболоид образуется движением изменяющегося эллипса по направляющей гиперболе вдоль действительной оси.

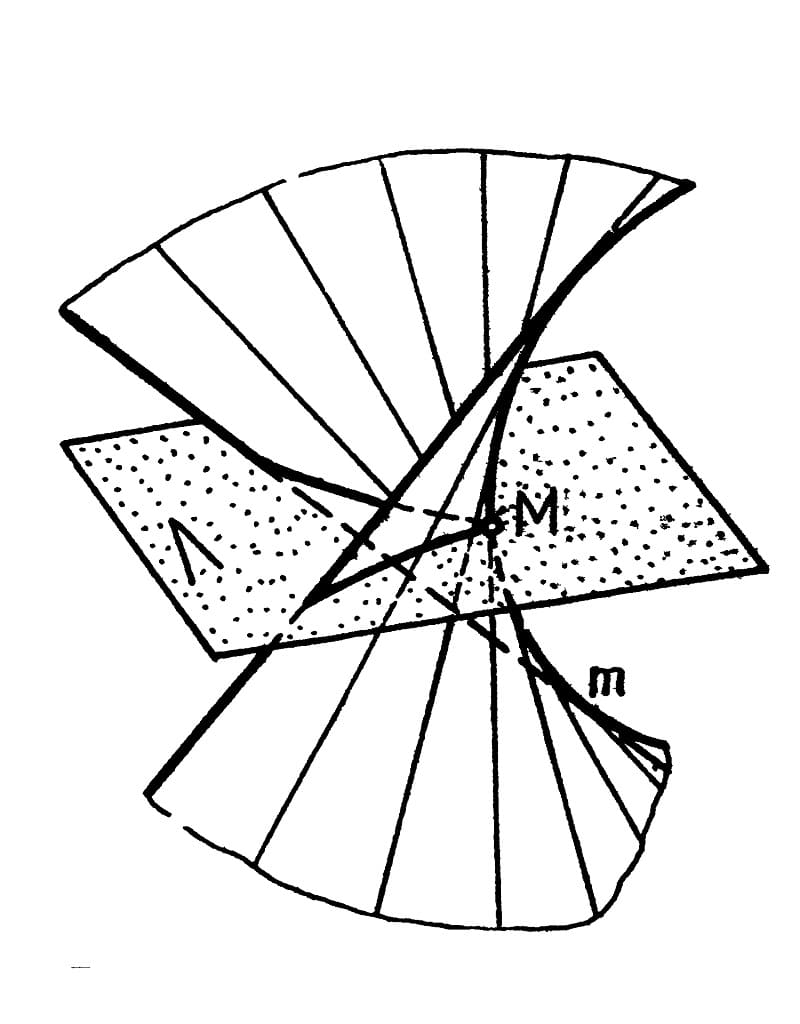
18. Точки и линии на поверхности.

Точка принадлежит поверхности, если она расположена на линии, принадлежащей поверхности. На поверхностях вращения в качестве таких линий удобно использовать параллели. Если на поверхности вращения (рис. 8.9) дана проекция М₂, то для нахождения параллели, которой принадлежит точка М, проводим через М фронтально-проецирующую плоскость s (М₂ ϵ s), такую что s ⊥ m. Тогда линия пересечения кривой поверхности с плоскостью s и даст искомую параллель. Радиус параллели равен расстоянию от оси вращения m₁ до точки поверхности 1₁. Этим радиусом проводим окружность с центром в точке m₁ (горизонтальной проекции оси вращения) и получаем горизонтальную проекцию параллели. На ней находим горизонтальные проекции точки М: М₁ — на видимой стороне кривой поверхности, а М’₁ — на невидимой.

Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности. Исключение составляет случай, когда линия представлена прямой, а поверхность — плоскостью. В этом случае для принадлежности прямой плоскости достаточно, чтобы хотя бы две точки ее принадлежали этой поверхности.

Если линия не принадлежит поверхности, то они пересекаются. Простейшим случаем является пересечение с поверхностью прямой линии. Задача решается путем заключения данной линии в какую-либо проецирующую плоскость и построением натуральной величины сечения, из которого легко определить точку входа и выхода прямой.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10654 —

Касательные плоскости, развертываемые поверхности

Для необходимых здесь выводов всегда предполагается, что они также существуют.

Чтобы вычислить вектор нормали в точке, нужны частные производные представления  : Икс(ты,v)знак равноc(ты)+vр(ты){\ displaystyle \ quad \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \; \ mathbf {r} (u)}

Икстызнак равноc˙(ты)+vр˙(ты) {\ displaystyle \ mathbf {x} _ {u} = \ mathbf {\ dot {c}} (u) + v \; \ mathbf {\ dot {r}} (u) \} ,Иксvзнак равнор(ты){\ displaystyle \ quad \ mathbf {x} _ {v} = \; \ mathbf {r} (u)}

пзнак равноИксты×Икстызнак равноc˙×р+v(р˙×р) .{\ displaystyle \ mathbf {n} = \ mathbf {x} _ {u} \ times \ mathbf {x} _ {u} = \ mathbf {\ dot {c}} \ times \ mathbf {r} + v (\ mathbf {\ dot {r}} \ times \ mathbf {r}) \.}

Поскольку скалярное произведение (позднее произведение с двумя равными векторами всегда равно 0!), В каждой точке есть касательный вектор . Касательные плоскости вдоль этой прямой идентичны, если они кратны . Это возможно только в том случае, если три вектора лежат в одной плоскости, т.е. ЧАС. линейно зависимы. Линейную зависимость трех векторов можно определить с помощью определителя этих векторов: п⋅рзнак равно{\ Displaystyle \ mathbf {п} \ cdot \ mathbf {r} = 0}р(ты){\ Displaystyle \ mathbf {r} (и_ {0})}Икс(ты,v){\ Displaystyle \ mathbf {х} (и_ {0}, v)}р˙×р{\ displaystyle \ mathbf {\ dot {r}} \ times \ mathbf {r}}c˙×р{\ displaystyle \ mathbf {\ dot {c}} \ times \ mathbf {r}}c˙,р˙,р {\ Displaystyle \ mathbf {\ точка {с}} \ ;, \; \ mathbf {\ точка {r}} \ ;, \; \ mathbf {r} \}

Касательные плоскости вдоль прямой совпадают, еслиИкс(ты0,v)знак равноc(ты0)+vр(ты0){\ displaystyle \ mathbf {x} (u_ {0}, v) = \ mathbf {c} (u_ {0}) + v \; \ mathbf {r} (u_ {0})}

Det(c˙(ты),р˙(ты),р(ты))знак равно .{\ displaystyle \ det (\ mathbf {\ dot {c}} (u_ {0}) \ ;, \; \ mathbf {\ dot {r}} (u_ {0}) \ ;, \; \ mathbf {r } (u_ {0})) \; = \; 0 \.}

Генеративная форма, к которой это применимо, называется торсальной .

Линейчатая поверхность точно тогда раскручивается в плоскость, когда для всех точек гауссова кривизна равна нулю. Это так тогда и только тогда, когдаИкс(ты,v)знак равноc(ты)+vр(ты){\ displaystyle \ quad \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \; \ mathbf {r} (u)}

Det(c˙,р˙,р)знак равно{\ displaystyle \ det (\ mathbf {\ dot {c}} \; \; \ mathbf {\ dot {r}} \ ;, \; \ mathbf {r}) \; = \; 0 \ quad}

применяется в каждой точке, d. т. е. если каждый образующий – торсальный. Поэтому развивающуюся область также называют торсом .

Свойства развертывающейся поверхности:

• Генераторы представляют собой семейство асимптотических линий , а также семейство линий кривизны .
• Разворачивающаяся поверхность – это либо (общий) цилиндр, либо (общий) конус, либо касательная поверхность (поверхность, состоящая из касательных пространственной кривой).

Определение и параметрическое представление [ править ]

Линейчатая поверхность, образованная двумя кривыми Безье как направляющими (красный, зеленый)

Двумерное дифференцируемое многообразие называется линейчатой ​​поверхностью , если оно представляет собой объединение однопараметрического семейства прямых. Линии этого семейства являются образующими линейчатой ​​поверхности.

Линейчатая поверхность может быть описана параметрическим представлением вида

(CR) .Икс(ты,v)знак равноc(ты)+vр(ты) , v∈р ,{\ displaystyle \ quad \ mathbf {x} (u, v) = {\ color {красный} \ mathbf {c} (u)} + v \; {\ color {blue} \ mathbf {r} (u)} \, \ v \ in \ mathbb {R} \,}

Любая кривая с фиксированным параметром является образующей (линией), а кривая – директрисой представления. Векторы описывают направления генераторов.
v↦Икс(ты,v){\ Displaystyle \; v \ mapsto \ mathbf {x} (u_ {0}, v) \;}тызнак равноты{\ displaystyle u = u_ {0}}ты↦c(ты){\ Displaystyle \; и \ mapsto \ mathbf {c} (и) \;}р(ты)≠{\ Displaystyle \; \ mathbf {r} (и) \ neq {\ bf {0 \;}}}

Директриса может схлопнуться в точку (в случае конуса см. Пример ниже).

В качестве альтернативы линейчатая поверхность (CR) может быть описана как

(CD) Икс(ты,v)знак равно(1-v)c(ты)+vd(ты) {\ displaystyle \ quad \ mathbf {x} (u, v) = (1-v) \; {\ color {красный} \ mathbf {c} (u)} + v \; {\ color {зеленый} \ mathbf {d} (u)} \}

со второй директрисой .
d(ты)знак равноc(ты)+р(ты){\displaystyle \;\mathbf {d} (u)=\mathbf {c} (u)+\mathbf {r} (u)\;}

В качестве альтернативы, можно начать с двух непересекающихся кривых в качестве директрис и получить по (CD) линейчатую поверхность с направлениями линийc(u),d(u){\displaystyle \mathbf {c} (u),\mathbf {d} (u)}r(u)=d(u)−c(u) .{\displaystyle \;\mathbf {r} (u)=\mathbf {d} (u)-\mathbf {c} (u)\ .}

Для создания линейчатой ​​поверхности двумя директрисами (или одной директрисой и векторами направлений линий) существенна не только геометрическая форма этих кривых, но и их специальные параметрические представления влияют на форму линейчатой ​​поверхности (см. Примеры a ), г)).

Для теоретических исследований более выгодно представление (CR) , поскольку параметр появляется только один раз.
v{\displaystyle v}

Линейчатые поверхности

Одним из объектов трехмерного пространства являются поверхности. Это непрерывное, бесконечное множество точек, которые имеют определенную, строго установленную, зависимость между координатами. Основными инструментами трехмерного моделирования служат различные способы их отражения.

В инженерной графике, начертательной геометрии есть метод, когда поверхность рассматривается как комплекс последовательных расположений линии, которая, подчиняясь определенному закону, перемещается в пространстве. Это кинематический способ, благодаря которому образуются геометрические объекты. Примером выступают технологические процессы, связанные с обработкой материала режущим инструментом. Плоскость получаемого изделия рассматривается как множество линий, эквивалентных (конгруэнтных) форме профиля резца режущего инструмента.

Для описания процесса образования используются два основных термина:

1. Образующая – это подвижная линия. Она, перемещаясь, может иметь постоянную форму. Если это кривая — получается нелинейчатая поверхность. Она относится к I классу. Когда образующая представлена прямой, это ведет к формированию линейчатой поверхности (II класс).
2. Направляющая – это неподвижная линия или плоскость, по ней движется образующая. Однозначно определить рассматриваемый объект возможно тремя линиями, задающими траекторию движения. Но, должно выполняться требование: две из трех линий задаются произвольно, третья – должна быть внутри конгруэнции, которая определяется уже выбранными двумя.

Такое перемещение не является хаотичным, оно подчиняется определенному закону. Законом может выступать перемещение вдоль неподвижных линий. Иными словами, образующая все время занимает конкретное установленное положение.

Определены следующие два вида линейчатых поверхностей:

• развертывающаяся;
• неразвертывающаяся (косая).

В пределах класса эти объекты, образованные перемещением прямой линии, подразделяются на:

1. Группы. Классификация на группы зависит от внешних условий движения образующей, то есть от количества направляющих.
2. Виды. Деление на виды по каждой группе определяется внутренними характеристиками движения – формой и относительным положением траекторий, по которым движется прямая.

Их образование может происходить вращением или поступательным передвижением образующей прямой. Цилиндры, конусы – примеры геометрических тел, образованных пересечением линейчатой поверхности вращения с областью, называемой основанием. Гранные объекты формируются поступательным передвижением образующей вдоль ломанных траекторий. Так образуются призмы и пирамиды.

7.12. Пересечение конуса плоскостью

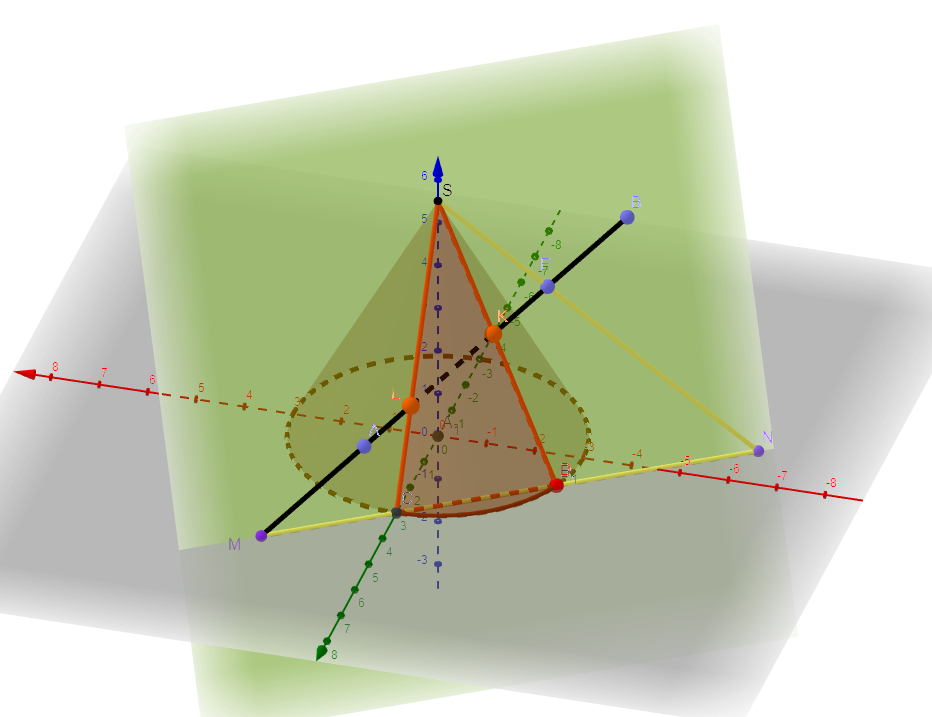
Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π₂ (Рисунок 7.16).

Рисунок 7.16

1. Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
2. Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
3. Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
4. Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
5. Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).

Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса

Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.

Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)

Рассмотрим пример построения сечения конической поверхности плоскостью.

Рисунок 7.19 – Построение пересечения конической поверхности плоскостью

Пусть задана секущая проецирующая плоскость σ⊥π₂ (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.

1. Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
2. Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π₂ и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π₁. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π₁ и π₃ совпадают с линиями проекционной связи.
3. На пересечении этих двух сечений на плоскости проекций π₁ строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
4. Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
5. Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.

На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.

7.10. Пересечение цилиндра плоскостью

Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).

1. Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
2. Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
3. Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.

Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):

Рисунок 7.15 – пересечение цилиндра плоскостью

1. Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
2. Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π₁ произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
3. Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π₃. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ₁ и откладываем его по соответствующей линии связи на π₃. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.

Линейчатые поверхности

Первыми известными человечеству поверхностями были плоскость (рис. 3.46 а), цилиндр (рис. 3.46 б), конус (рис. 3.46 в) и сфера (рис. 3.46 г). Архимед присоединил к этому списку «коноиды» (рис. 3.46 д) и «сфероиды» (рис. 3.46 е).

Виды поверхностей

Только П. Ферма у 1643 г. сделал существенный шаг в теорию поверхностей. Он рассматривал любую поверхность как упорядоченную совокупность точек и линий пространства и дал классификацию поверхностей по их характерным признакам.

В 1655 р. Дж. Уоллис определил объёмы и центры тяжести тел, ограниченных кривыми поверхностями.

Наиболее применимыми являются такие способы задания поверхностей:

а) аналитический, в котором поверхность задаётся уравнением f(x,y,z) = 0,  связывающим координаты х, у, z каждой точки поверхности;

б) кинематический, согласно которому поверхность создаётся непрерывным движением одной линии l (образующей) вдоль неподвижной линии  (направляющей);

в) каркасный – с помощью множеств характерных точек А (1) , А (2) , … и линий l (1) , l (2) , … поверхности.

Примеры геометрического, кинематического и каркасного способов задания поверхности Ф приведены на рис. 3.47 а – в.

Комплексный чертёж поверхности Ф считается заданным, если одновременно выполняются такие условия:

а) можно построить три проекции l1, l2, l3 образующей линии l;

б) по одной проекции М1 точки М поверхности можно определить другие две её проекции;

в) по двум проекциям А1, А2 точки А на комплексном чертеже можно определить,  принадлежит ли она поверхности Ф, или не принадлежит.

Джон Уоллис (John Wallis) – английский математик, один из предшественников математического анализа, тригонометрии, теории чисел. В 1655 г. издал трактат «Арифметика бесконечного», где ввёл символ бесконечности  и рассчитал интегральные суммы (ещё до существования понятия про интеграл). Ввёл современное понятие математической операции  логарифмирования.

Способы задания поверхностей

Комплексный чертёж поверхности

Например, на рис. 3.48 можно установить проекции образующей l, определить фронтальную проекцию М2 точки М по известной проекции М1. По комплексному чертежу точки А однозначно определяется, что она не принадлежит поверхности. Таким образом, удовлетворив все условия, делается вывод о том, что на рис. 3.48 построен чертёж поверхности Ф.

Разнообразие форм поверхностей создаёт трудности при их изучении. Поэтому целесообразно сделать систематизацию поверхностей. Современное развитие теории поверхностей позволяет классифицировать поверхности по многим критериям. С позиции начертательной геометрии классификация поверхностей такая:

а) линейчатые – поверхности, образованные прямолинейной образующей l:

1) с тремя направляющими – образованы движением образующей l, которая одновременно пересекает три направления 

– линейчатая поверхность общего вида;

– конусоид; – косой цилиндр;

– однополостной гиперболоид;

2) с двумя направляющими (див. п. 3.2.1.2):

– цилиндроид;

– коноид;

– гиперболический параболоид;

– геликоид;

3) с одной направляющей (см. п. 3.2.1.3):

– плоскость;

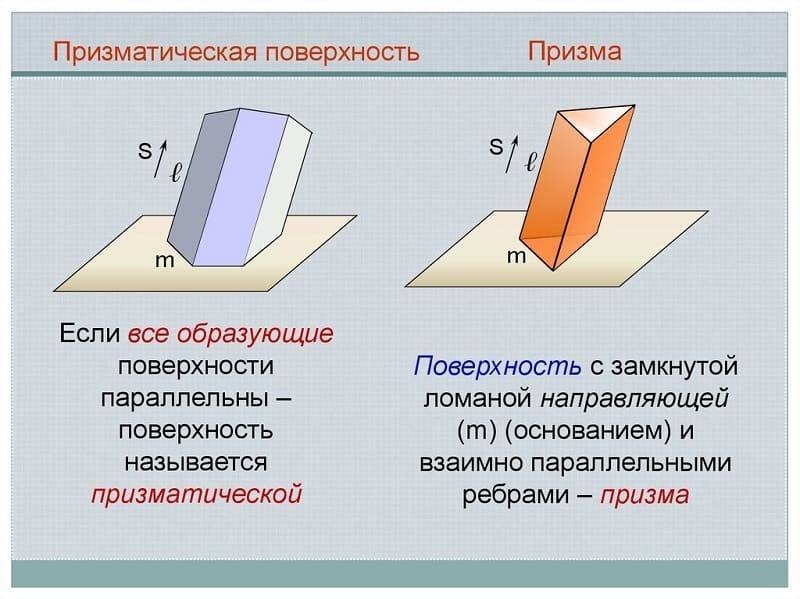
– цилиндр и призма;

– конус и пирамида;

– торс;

б) нелинейчатые:

1) с переменной образующей (см. п. 3.2.2.1);

– поверхность общего вида;

– каналовая поверхность;

2) с постоянной образующей (см. п. 3.2.2.2):

– трубчатая поверхность;

– поверхность перенесения;

– поверхность вращения.

Линейчатая поверхность общего вида – поверхность, образованная движением прямолинейной образующей l, которая в каждом своём положении пересекает три кривые направляющие  (рис. 3.49 а).

Линейчатые поверхности с тремя направляющими

Конусоид – поверхность, образованная движением прямолинейной образующей l,, которая в каждом своём положении пересекает две криволинейные направляющие  и одну прямолинейную направляющую  (рис. 3.49 б).

Косой цилиндр – поверхность, образованная движением прямолинейной образующей l,, которая в каждом своём положении пересекает одну криволинейную направляющую  и две прямолинейные направляющие  (рис. 3.49 в).

Однополостной гиперболоид – поверхность, образованная движением прямолинейной образующей l, которая в каждом своём положении пересекает три прямолинейные направляющие  (рис. 3.49 г).

Линейчатые поверхности широко используются в проектировании архитектурных сооружений башен, павильонов, каркасов крыш зданий и т.д..

На рис. 3.50 приведены примеры сооружений, построенных по методу В. Г. Шухова – ученого, который впервые предложил строить каркасы сооружений в форме однополостного гиперболоида.

Сооружения, построенные по методу В. Г. Шухова

7.2. Поверхности вращения

Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).

Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.

Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.

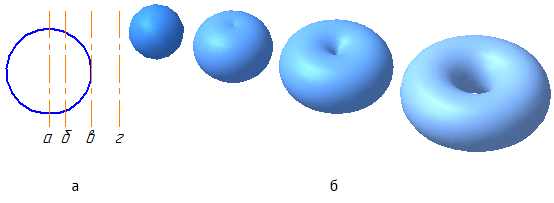
Рисунок 7.4 – Образование поверхностей вращения

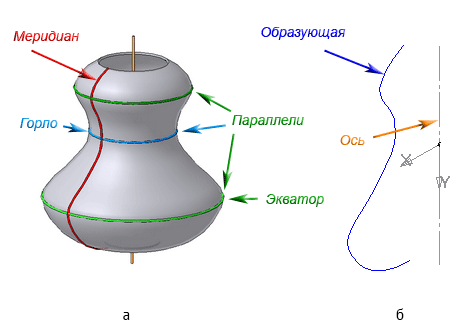
Рисунок 7.5 – Элементы поверхности вращения

Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).

Наименьшая параллель называется горлом, наибольшая – экватором.

Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом.

Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом.