Модуль зубьев зубчатого колеса

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Зубчатые передачи. Их достоинство и недостатки. область применение, классификации.

Зубчатые передачи.

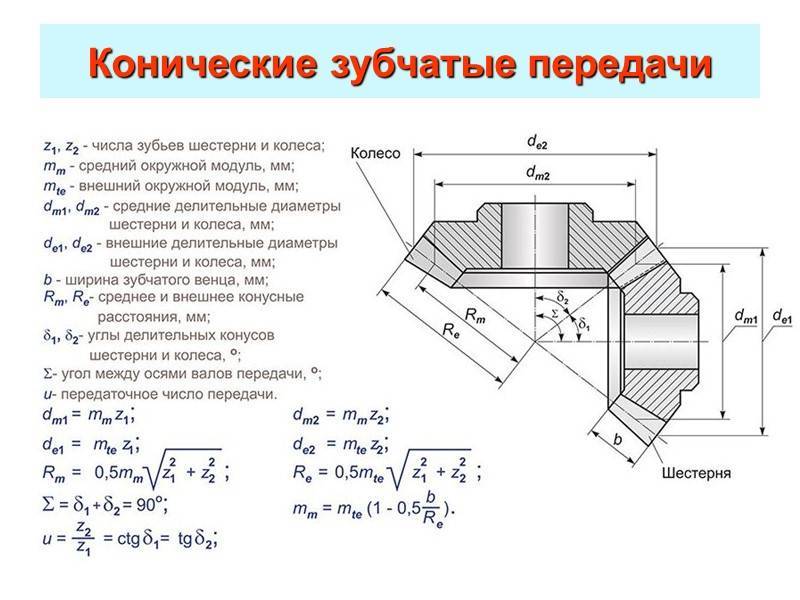
Зубчатая передача — это механизм или часть механизма в состав которого входят зубчатые колёса. Движение пе-редаётся с помощью зацепления пары зубчатых колёс. Меньшее зубчатое колесо принято называть шестерней, большее – колесом. Параметрам шестерни приписывают индекс 1, параметрам колеса – индекс 2.

Достоинства и недостатки зубчатых передач

Достоинства зубчатых передач: • Возможность применения в широком диапазоне скоростей, мощностей и передаточных отношений. • Высокая нагрузочная способность и малые габариты. • Большая долговечность и надёжность работы. • Постоянство передаточного отношения. • Высокий КПД (87-98%). • Простота обслуживания. Недостатки зубчатых передач: • Большая жёсткость не позволяющая компенсировать динамические нагрузки. • Высокие требования к точности изготовления и монтажа. • Шум при больших скоростях.

Классификация зубчатых передач

По передаточному отношению: • с постоянным передаточным отношением; • с переменным передаточным отношением. По форме профиля зубьев: • эвольвентные; • круговые (передачи Новикова); • циклоидальные. По типу зубьев: • прямозубые; • косозубые; • шевронные; • криволинейные. По взаимному расположению осей валов: • с параллельными осями (цилиндрические передачи с прямыми, косыми и шевронными зубьями); • с пересекающимися осями (конические передачи); • с перекрещивающимися осями. По форме начальных поверхностей: • цилиндрические; • конические; • гиперболоидные; По окружной скорости колёс: • тихоходные; • среднескоростные; • быстроходные. По степени защищенности: • открытые; • закрытые. По относительному вращению колёс и расположению зубьев: • внутреннее зацепление (вращение колёс в одном направлении); • внешнее зацепление (вращение колёс в противоположном направлении).

Виды разрушений зубьев

2. Заедание зубьев наблюдается в высоконагруженных и высокоскоростных зубчатых, а также червячных передачах.

В местах контакта из-за трения развивается высокая температура, способствующая снижению вязкости масла, разрыву масляной пленки и образованию металлического контакта зубьев. Происходит молекулярное сцепление (микросварка) частиц металла. Растет сопротивление вращению, наросты металла на зубьях задирают рабочие поверхности сопряженных зубьев.

3. Поломка зубьев. Причина – напряжение изгиба σ_F. Это основной вид разрушения высокотвердых (Н ≥ 56 HRC) и открытых передач.

В открытых передачах в результате плохой смазки и абразивного истирания поверхностей зубьев от грязи выкрашивание не успевает развиться, но уменьшаются размеры сечений зубьев, растут напряжения изгиба σ_F. Возрастают зазоры, удары, шум. Усталостная поломка в этом случае связана с развитием трещин 3 на растянутой стороне ножки зуба (рис.4.3, б). В высокотвердых передачах зубья хрупкие, поверхность их имеет хорошее сопротивление выкрашиванию, но хуже противостоит прогрессирующему трещинообразованию в основании зуба.

4. Смятие рабочих поверхностей (пластические сдвиги) или хрупкое разрушение (Н ≥ 56 HRC) зубьев при кратковременных значительных перегрузках или ударном приложении нагрузки.

5. Отслаивание твердого поверхностного слоя при значительных контактных напряжениях и зарождении усталостных трещин в глубине под упрочненным слоем.

Обозначения для расчёта шестерней по формулам.

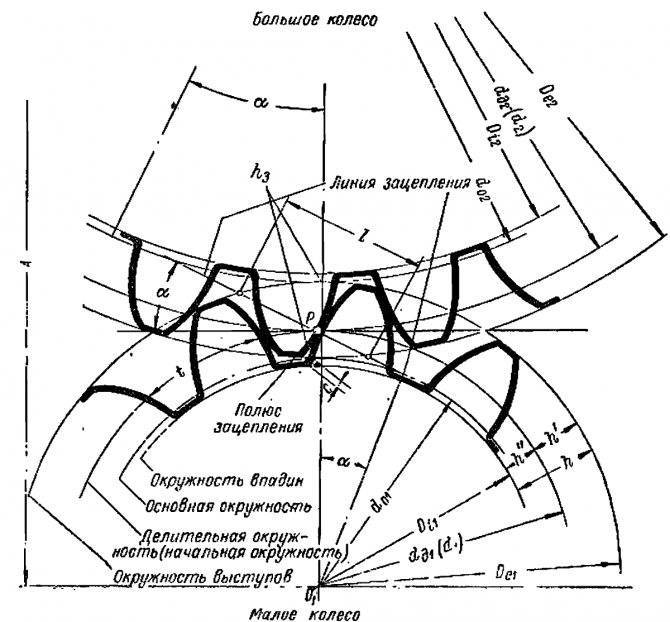
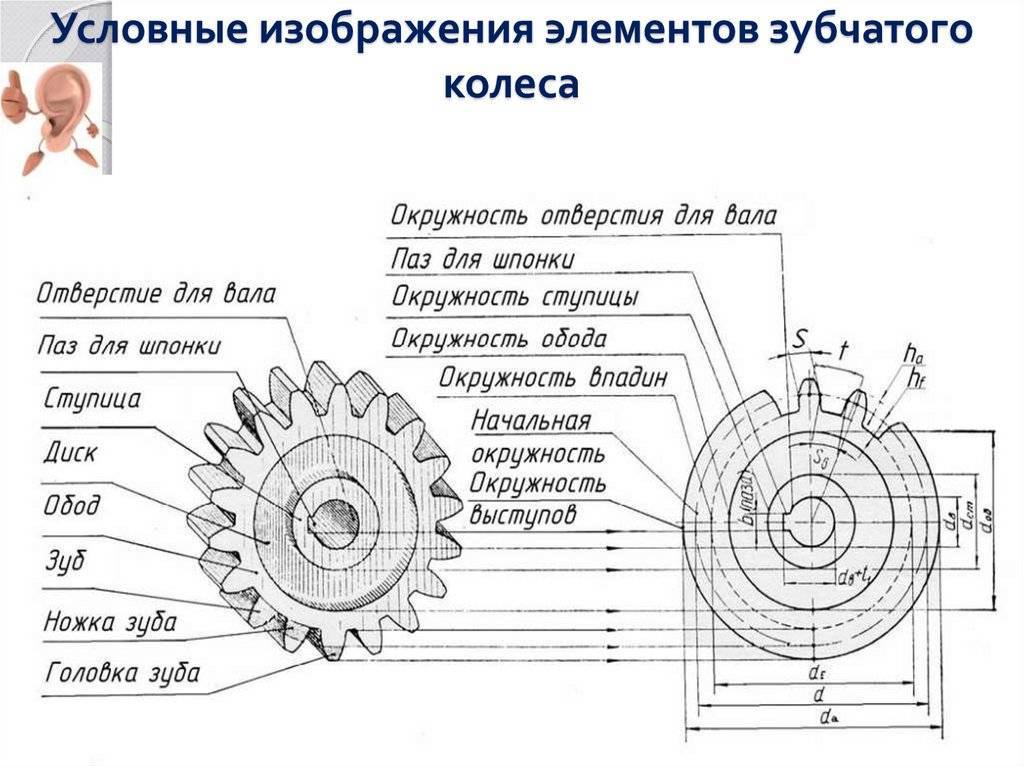
К вашему вниманию все обозначения какие вам понадобятся для расчета по формулам параметров шестерней. В данной таблице представлены основные обозначения параметров цилиндрических зубчатых колес:

• Высота зуба (полная).
• Высота головки зуба от окружности выступов до делительной окружности.
• Высота ножки зуба от делитель-ной окружности до окружности впадин.
• Глубина замера толщины зуба.
• Глубина захода зубьев, равная сумме высот головок зубьев (рабочая высота зуба).
• Диаметр начальной окружности.
• Диаметр делительной окружности.
• Диаметр основной окружности.
• Диаметр окружности выступов.
• Диаметр окружности впадин.
• Длина зацепления.
• Зазор радиальный в зубчатой паре.
• Зазор боковой в зубчатой паре.
• Зазор боковой в торцовом сечении.
• Зазор боковой в нормальном сечении.
• Коэффициент сдвига осей.
• Коэффициент высоты зуба инструмента (исходного контура).
• Коэффициент высоты зуба инструмента по отношению к модулю в нормальном, сечении.
• Коэффициент высоты зуба инструмента по отношению к модулю в торцовом сечении.
• Коэффициент сдвига исходного контура (инструмента).
• Коэффициент сдвига исходного контура (инструмента) минимальный при котором нет подрезания.
• Коэффициент сдвига исходного контура максимальный.
• Коэффициент сдвига исходного контура (инструмента) при заостренных зубьях.
• Коэффициент перекрытия.
• Коэффициент перекрытия в торцовой плоскости для косозубых колес.
• Модуль торцовый.
• Модуль нормальный.
• Межцентровое (межосевое) расстояние сцепляющейся пары колес.
• Межцентровое расстояние фаузацепления .
• Питч диаметральный.
• Питч окружной.
• Половина угловой толщины зуба на делительной окружности.
• Разность сдвигов—разность коэффициентов коррекции при внутреннем зацеплении.
• Сумма сдвигов исходного контура.
• Сумма коэффициентов коррекции сцепляющихся колес.
• Сумма чисел зубьев сцепляющихся колес при внутреннем зацеплении.
• Сумма чисел зубьев сцепляющихся колес при наружном зацеплении.
• Толщина зуба номинальная по хорде делительной окружности.
• Толщина зуба по дуге делительной окружности номинальная (без обязательного утонения) — для прямозубых колес.
• Толщина зуба номинальная по постоянной хорде для прямозубых колес.
• Толщина зуба номинальная по постоянной хорде для косозубых колес в нормальном сечении.
• Толщина зуба номинальная по постоянной хорде для косозубых колес в торцовом сечении.
• Толщина зуба по дуге окружности выступов.
• Толщина, зуба по постоянной хорде верхний предельный размер.
• Толщина зубьев по общей нормали для прямозубых колес .
• Толщина зубьев по общей нормали для прямозубых колес (или реек) — верхний предельный размер.
• Толщина зубьев по общей нормали для косозубых колес в нормальном сечении.
• Толщина зубьев по общей нормали для косозубых колес в нормальном сечении — верхний предельный размер.
• Угол зацепления пары колес.
• Угол зацепления косозубых колес в торцовом сечении.
• Угол инструмента профильный (исходного контура).
• Угол инструмента в нормальном сечении профильный.
• Угол инструмента в,торцовом сечении профильный.
• Угол наклона зубьев на основном цилиндре.
• Угол наклона зубьев на делительном цилиндре.
• Число зубьев.
• Число зубьев колеса, свободного от подрезания, минимальное.
• Число зубьев колеса практически допускаемое минимальное.
• Число зубьев, охватываемых размером.
• Шаг по делительной окружности.
• Шаг основной.
• Шаг торцовый.
• Шаг нормальный.
• Ширина зубчатого венца.

Заказ: Шестерня, диск. Модуль шесть.

Предыдущая запись

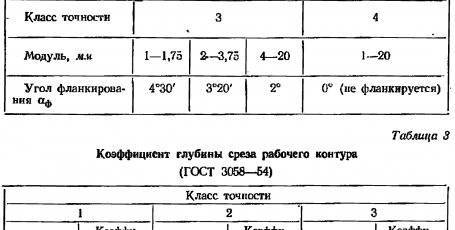
Исходный контур зубчатых колёс.

Следующая запись

Параметры модуля шестерни

Рассматриваемая характеристика обозначается литерой m, указывает на прочность зубчатых передач. Единица измеряется в миллиметрах (чем выше нагрузка на передачу, тем больше модульное значение). В расчете параметра используются следующие показатели:

• диаметр делительной окружности;
• шаг и число зубьев;
• эвольвент (диаметр основной окружности);
• аналогичная характеристика впадин темной шестеренки;
• высота зуба темного и светлого колеса.

В машиностроительной отрасли расчеты ведутся по стандартным значениям для удобства изготовления и замены шестерен с числами от 1-го до 50-ти.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Применение

Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить  число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.

С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.

Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.

Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма.  Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.

Зубчатые колеса используются также  для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.

Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой  массой и стоимостью.

Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач,  отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.

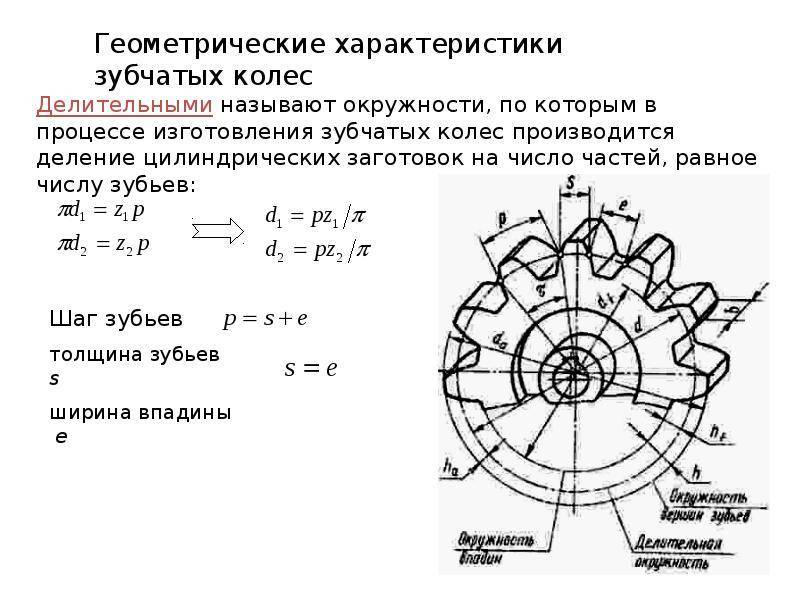
Цилиндрические зубчатые колёса [ править | править код ]

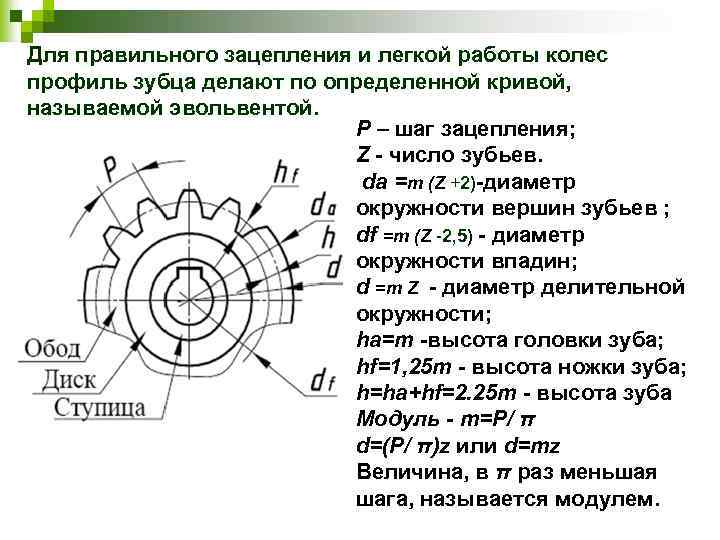
Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

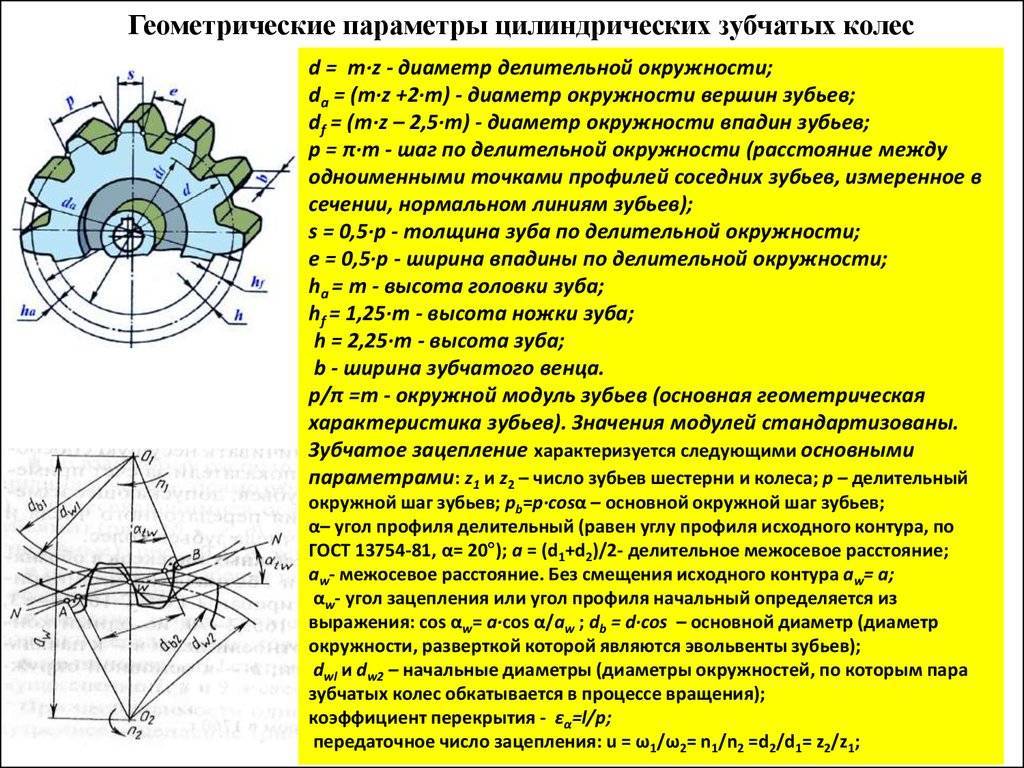
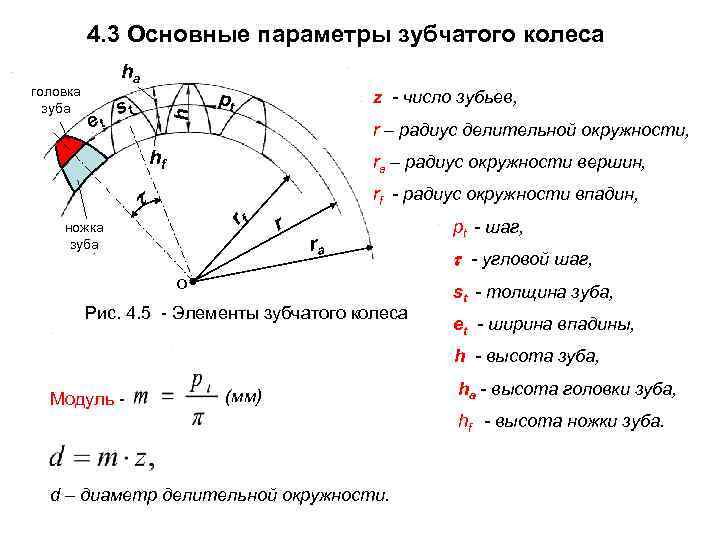
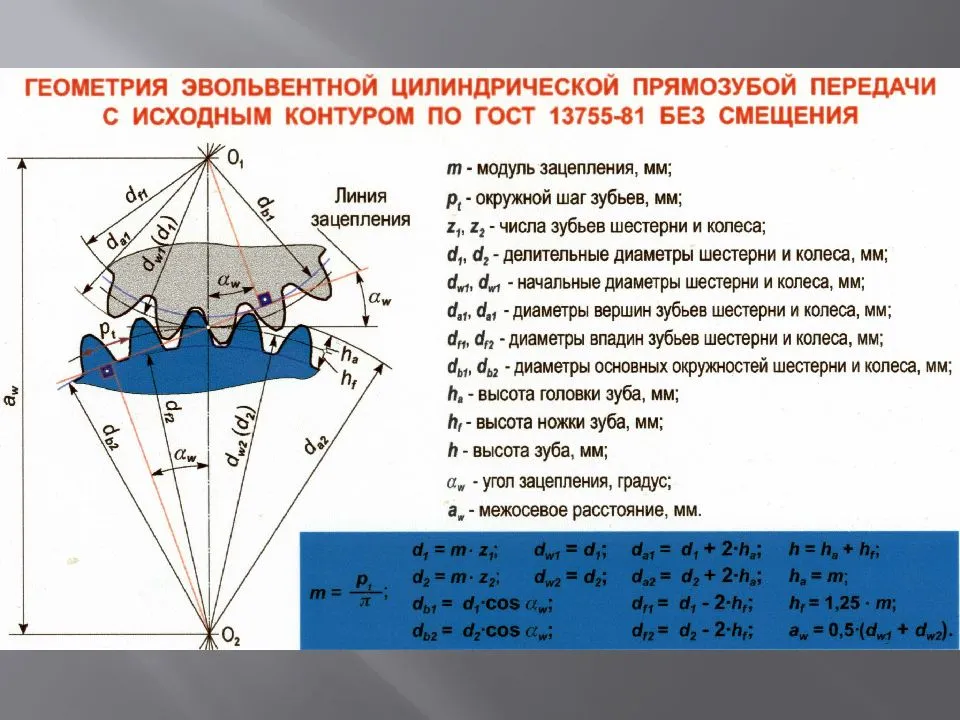
Параметры эвольвентного зубчатого колеса:

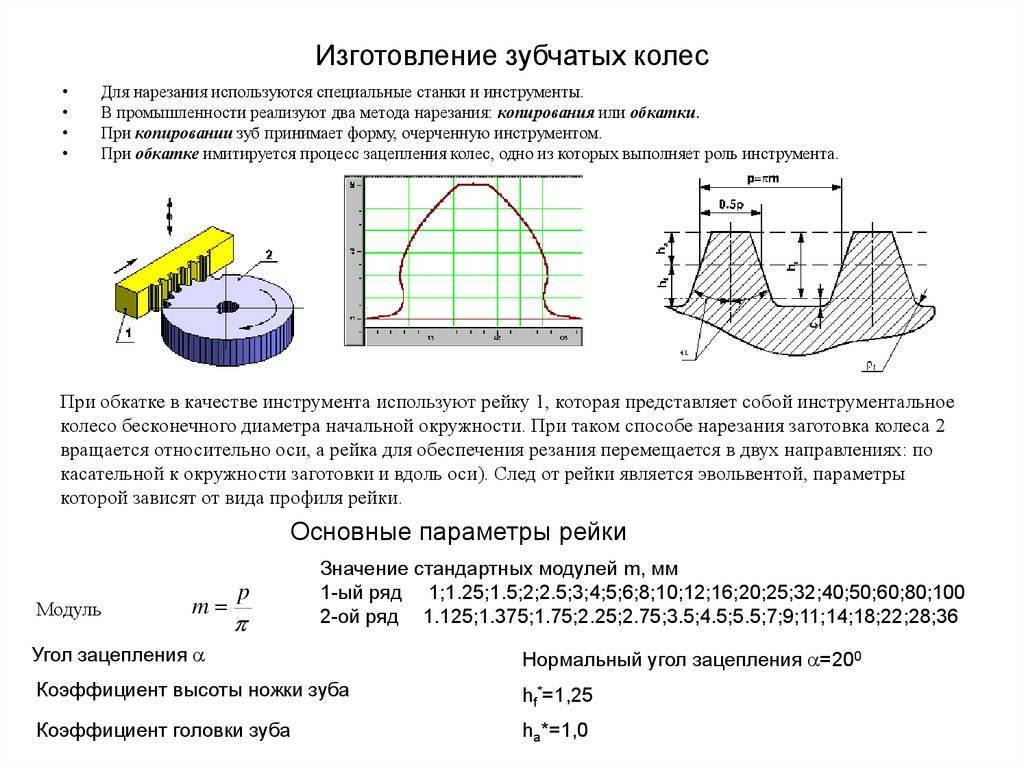
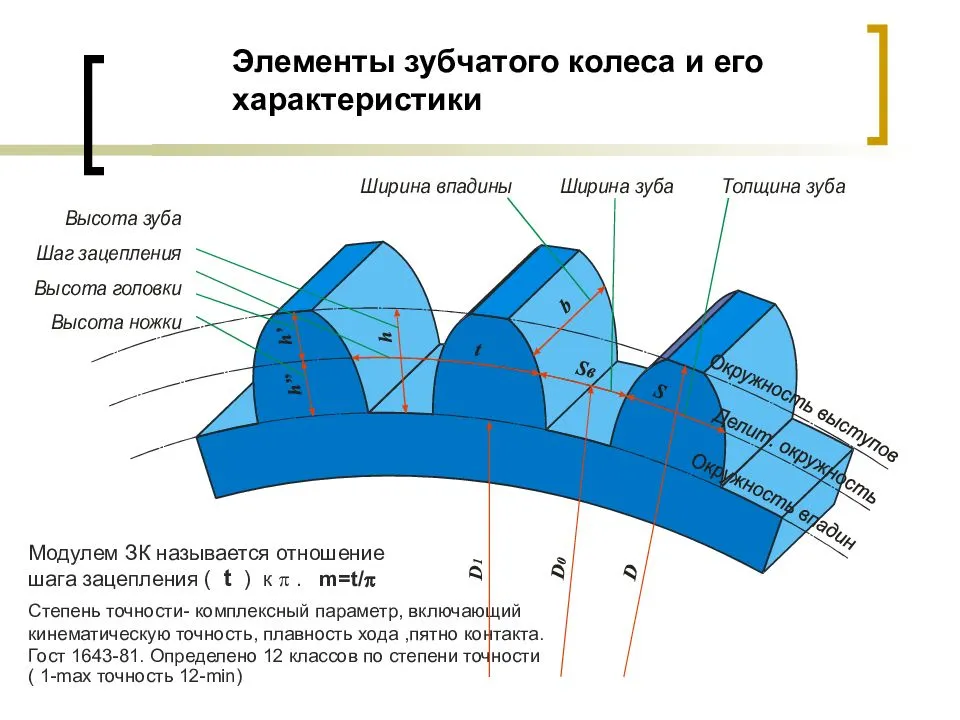
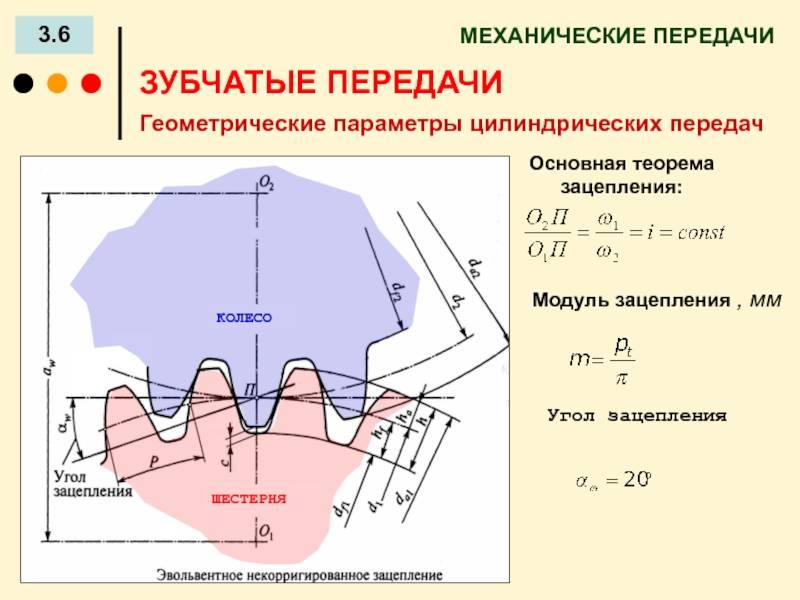
m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

>> >

• z — число зубьев колеса
• p — шаг зубьев (отмечен сиреневым цветом)
• d — диаметр делительной окружности (отмечена жёлтым цветом)
• d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
• d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
• d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
• h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определённые значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае т. н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с «нулевыми» зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. отрицательным смещением, а смещение дальше от заготовки наз. положительным) соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

h f P h a P = 1 , 25 >>>=1,25> >

Отсюда получаем, что высота зуба h (на рисунке не обозначена):

h = h f P + h a P = 2 , 25 m >+>=2,25m> >

Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

m = d a z + 2 >> >

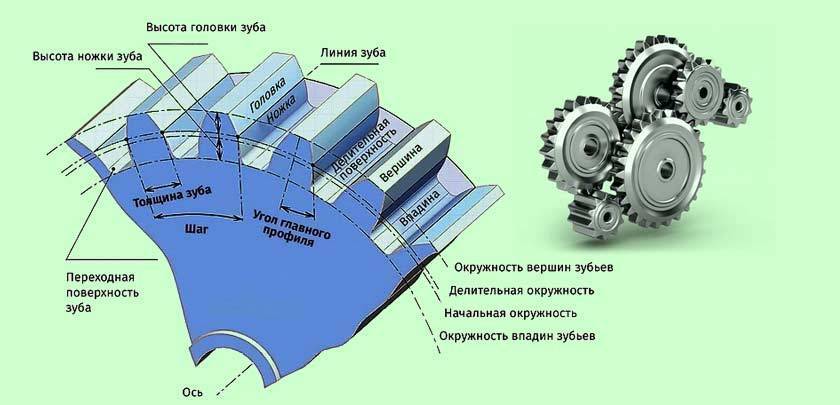
Продольная линия зуба

Зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:

17. Длина общей нормали цилиндрических прямозубых колес

Измерение толщины зубьев при длине общей нормали W имеет то преимущество перед измерением по постоянной хорде, что не требуется более точного изготовления зубчатых колес по наружному диаметру.

Для прямозубых колес без смещения

для колес со смешением (при коэффициенте смещения х)

здесь W’ — длина общей нормали цилиндрических прямозубых колес при m_n = 1. Значения W’ в зависимости от числа зубьев колеса и числа зубьев, охватываемых при измерении, указаны в таблице, приведенной ниже.

Дайна общей нормали W’ цилиндрических прямозубых колес при m_n = 1 мм

Как рассчитать показатель?

Определение модуля шестерни фиксируется по следующей формуле:

• m = d/z = p/.
• Высота головки зуба и аналогичный параметр ножки отмечаются символами Hfp и Hap, соотношение — Hfp/Hap = 1,24.
• Как определить модуль шестерни другим способом? m = da/z+2.

Часто перед инженерами возникает задача по оцениванию шестерни в реальном исполнении для замены или починки. Иногда документация на деталь составляется формально, что усложняет проведение указанных манипуляций. Среди проверенных методов диагностики — способ обкатки. Зубчатое колесо с известными параметрами вставляют в зубья тестируемого элемента, после чего проводят круговую обкатку. Если испытуемая пара входит в зацепление, это свидетельствует о совпадении шага. При негативном результате процесс повторяют. С косозубыми вариациями выбирают фрезу, точно подходящую по шагу.

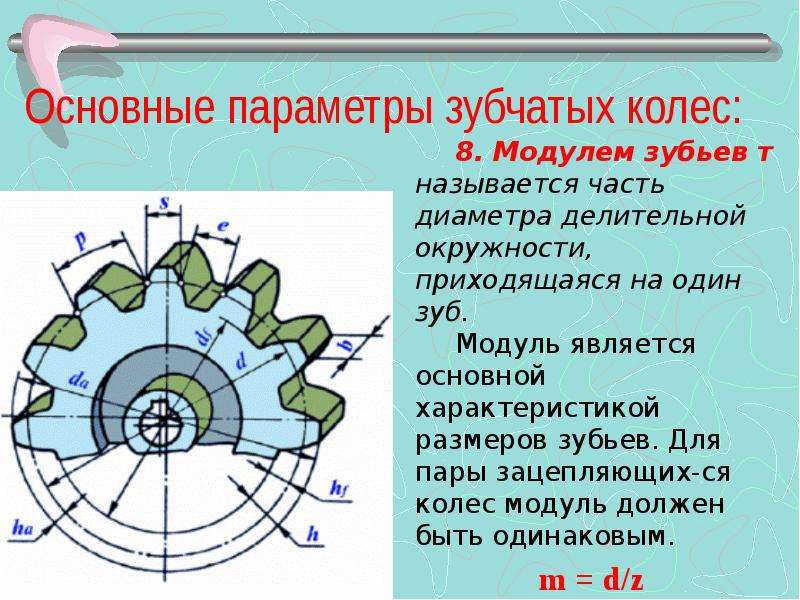
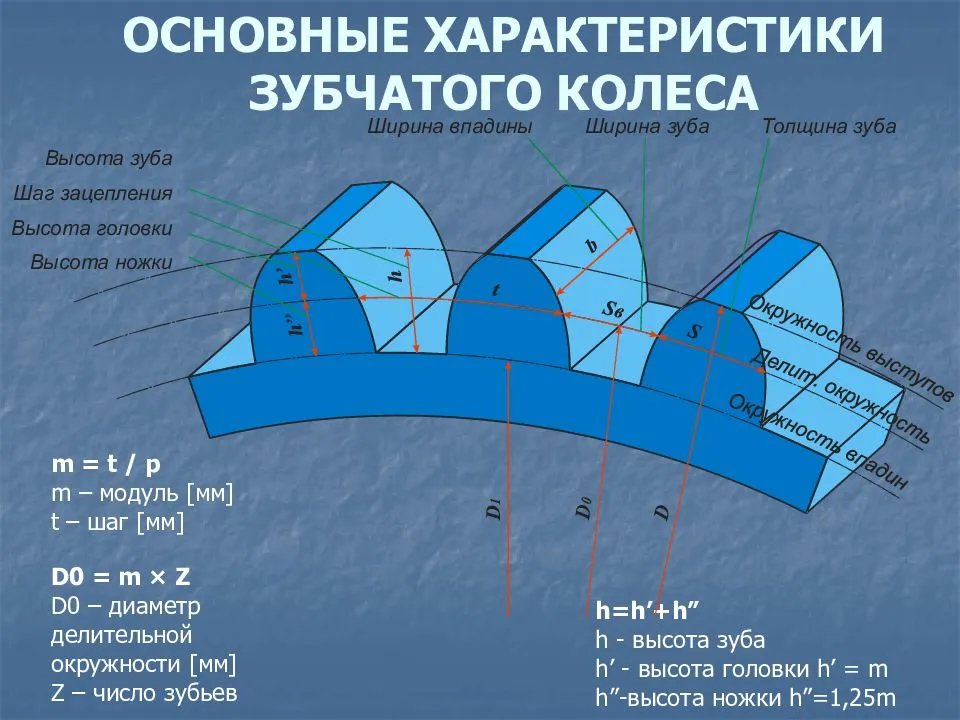
Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

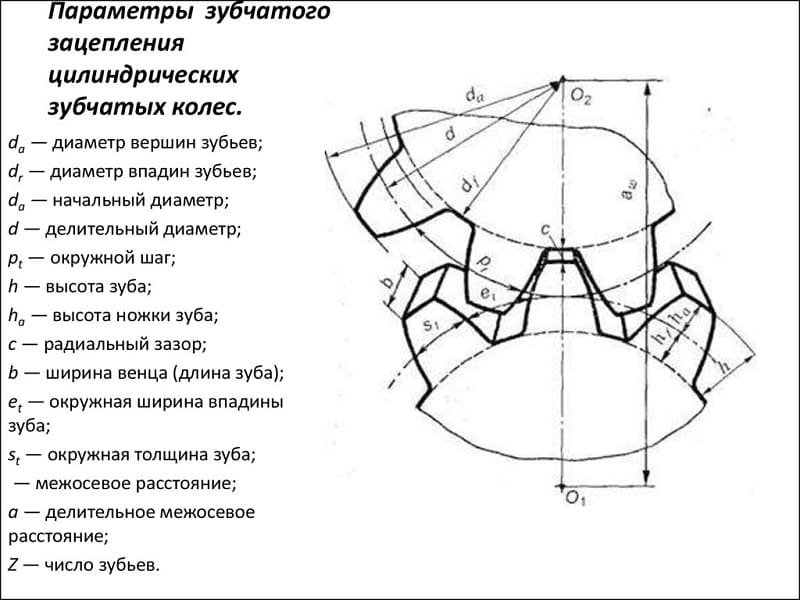
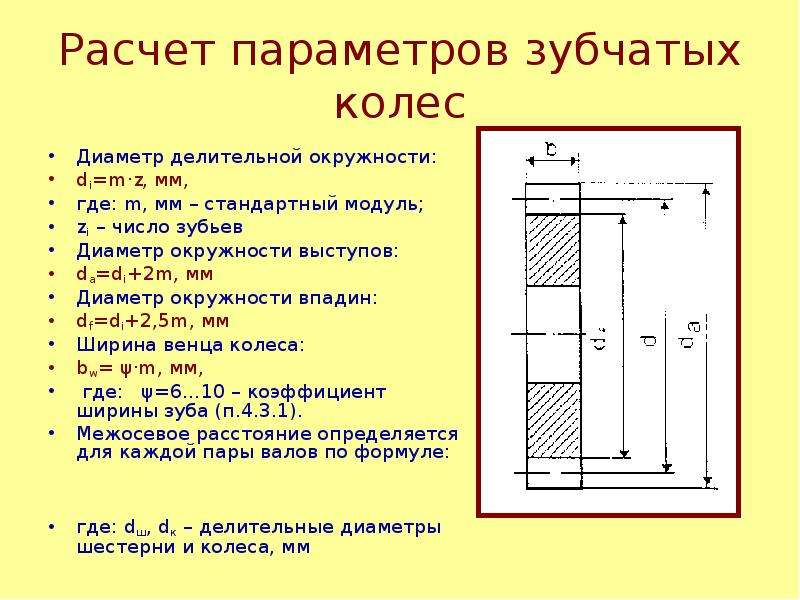
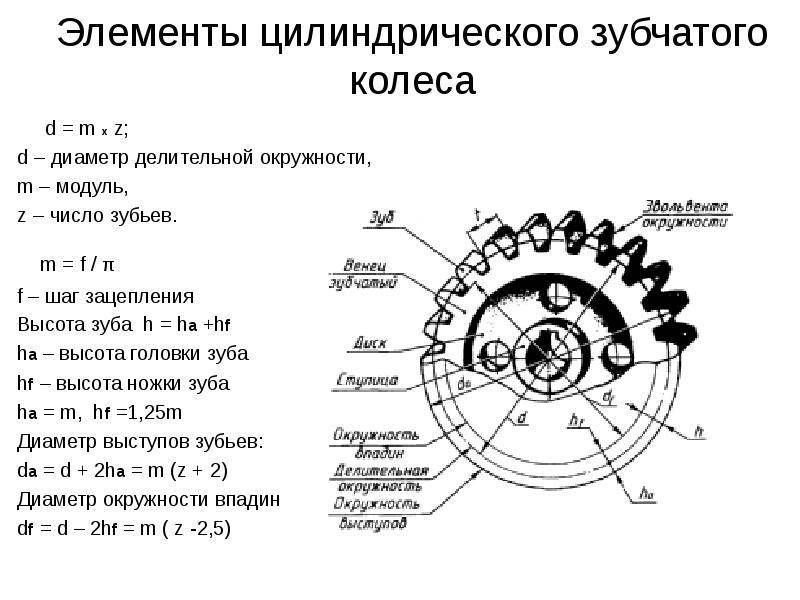
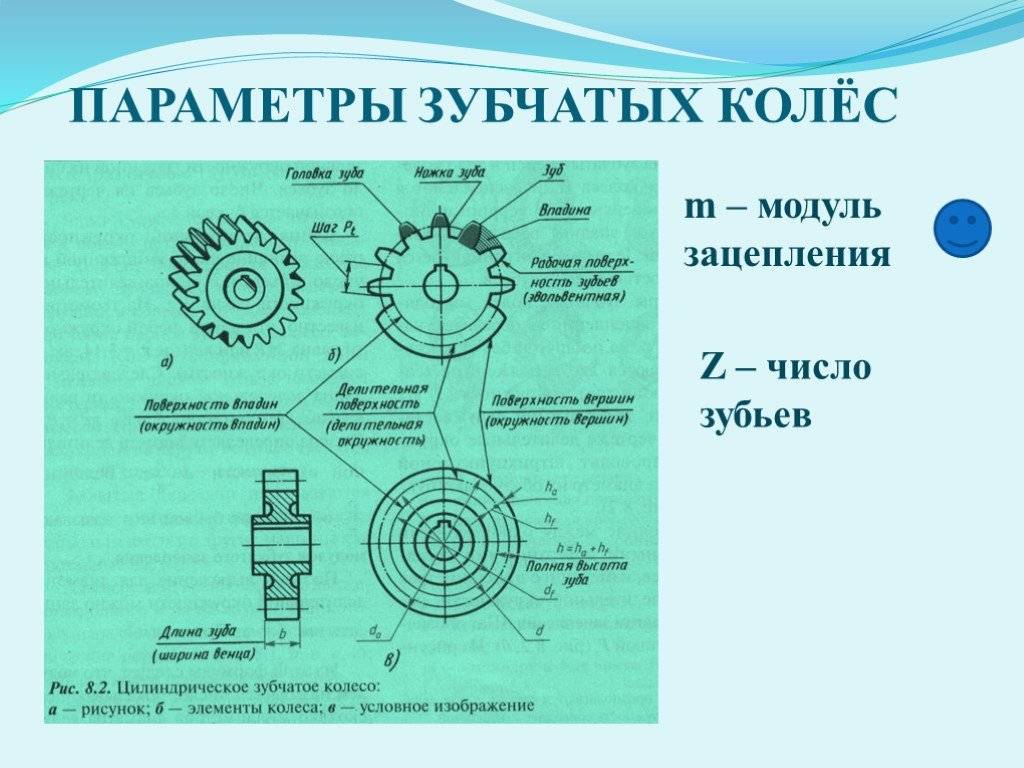
Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

где h — высота зубца.

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

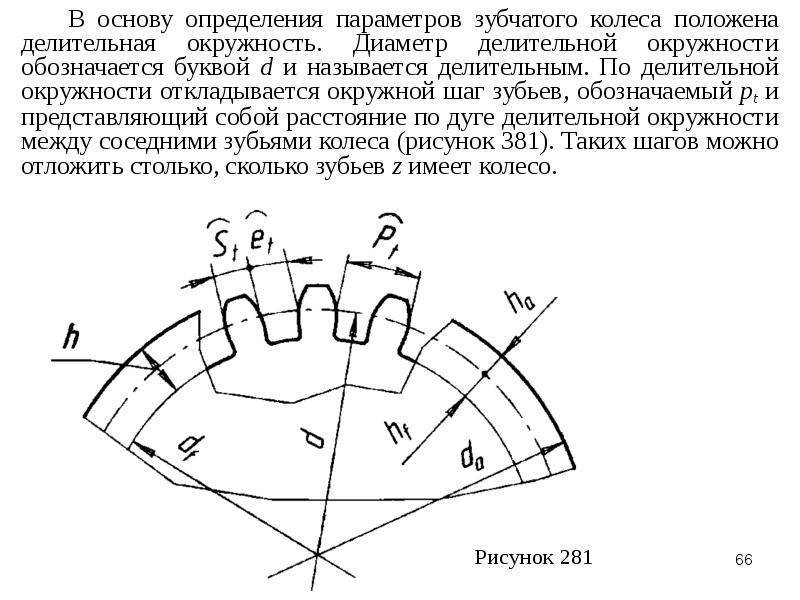
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t× z,

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

Диаметр окружности впадин D i соответствует D e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Выполнив подстановку в правой части равенства, имеем:

D i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D i = m(z-2,5m).

Полная высота:

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s в, получаем формулы для ширины впадины

• для отлитых зубцов: s в =πm-1,53m=1,61m:
• для выполненных путем фрезерования- s в = πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

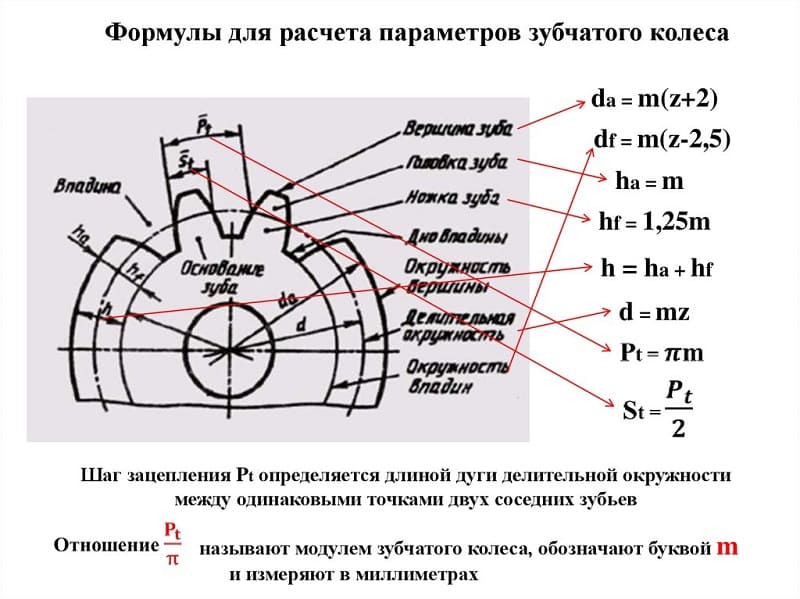
Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

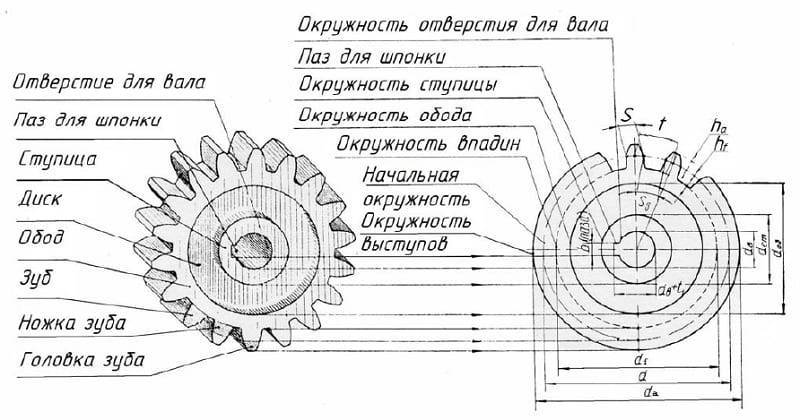
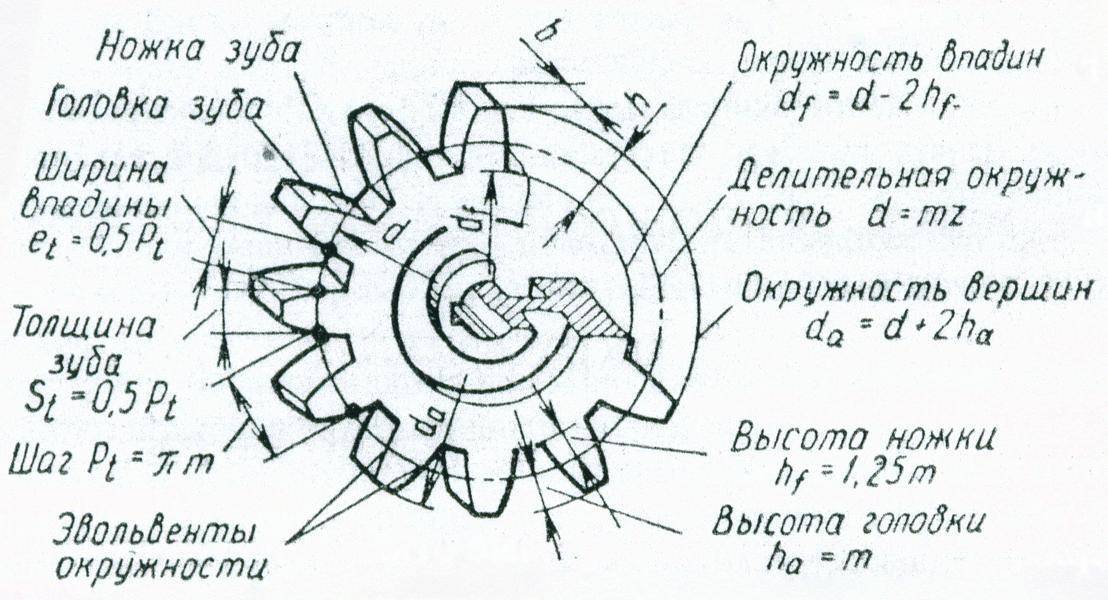
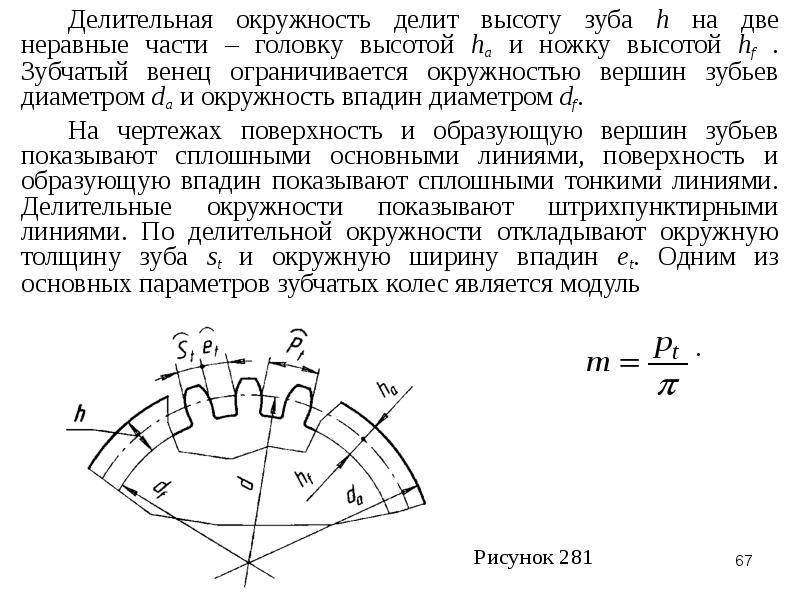
Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.