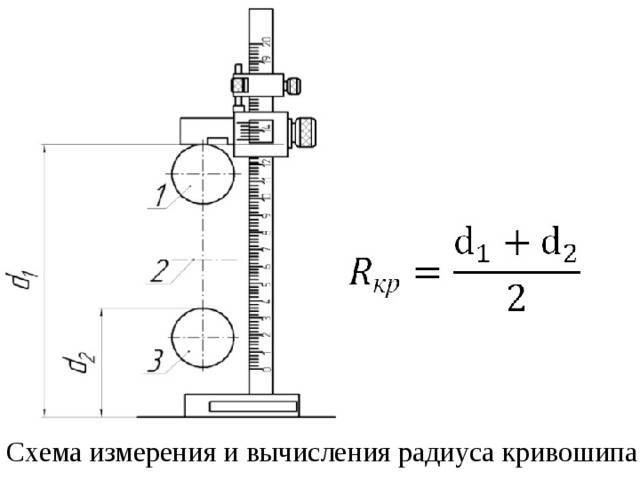
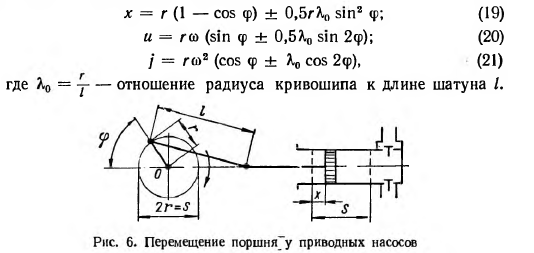
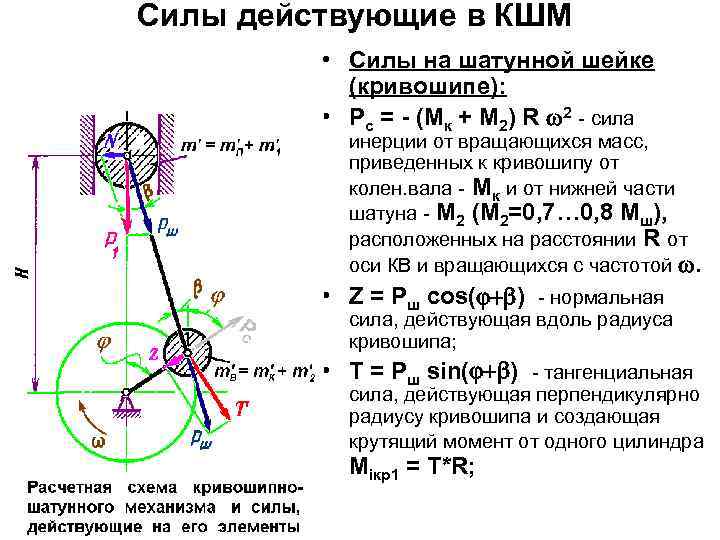
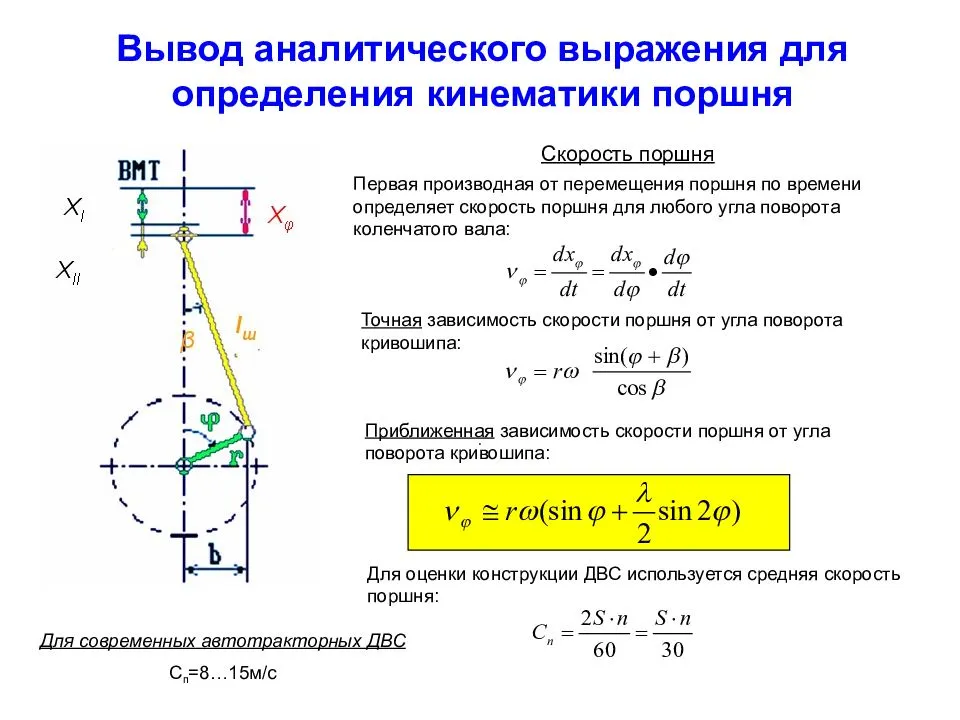
6.4 Определение ускорения поршня
Уравнение ускорения поршня может быть получено дифференцированием уравнения скорости по t.
При
Вывод:
а) При φ=180°; и λ<0,25 кривая ускорения выпуклая и ускорение имеет одно наименьшее значение
б) При λ>0,25 в точке кривая ускорения имеет вогнутость в сторону оси и ускорение дважды достигает наименьшего значения
Построение кривой ускорения поршня произведено:
а) аналитически. При этом значение множителя Aj в скобках справочная величина в зависимости от λ и φ.
б) графически. Путем сложения ускорения первого jП I=ω2Rcosφ и второго jП II=ω2Rλcos2φ
Для дезаксиального механизма jП
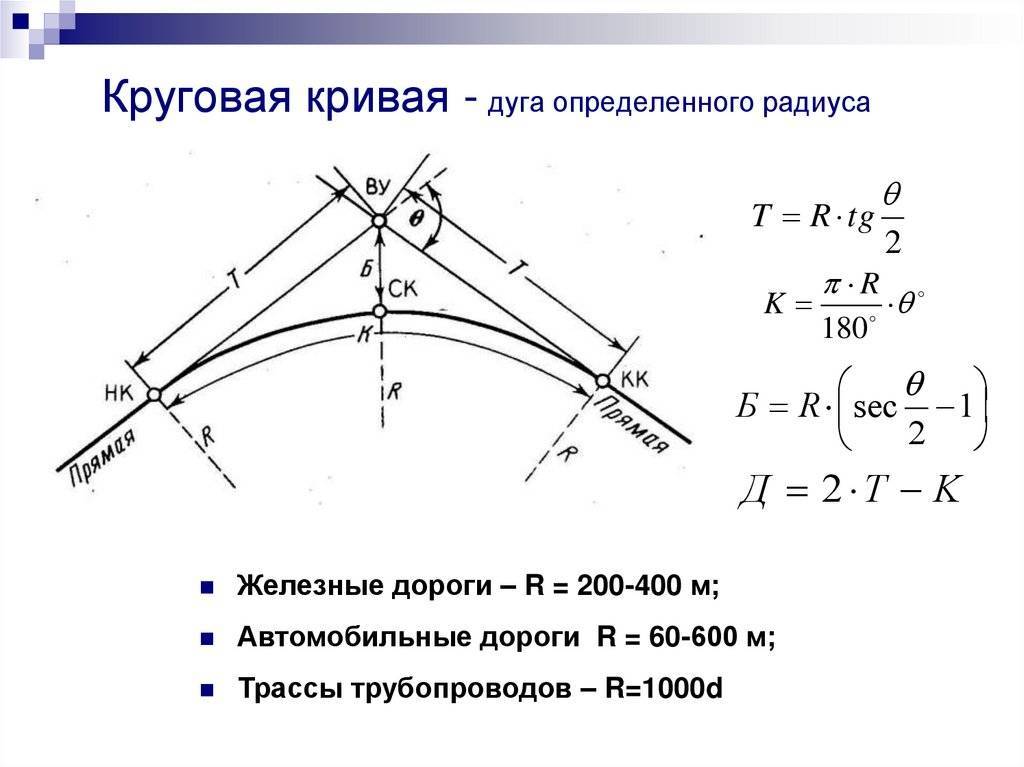
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье “Расчет арочной перемычки”, поэтому здесь лишь приведу основные формулы:
tg(a/4) = 2Н/L (278.1.2)
тогда
а/4 = arctg(2H/L)
R = H/(1 – cos(a/2)) (278.1.3)
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад – для того, чтобы напомнить формулы – есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Система охлаждения поршней мотоцикла
Существует четыре пути охлаждения поршня, первым из которых являются поршневые кольца.
- Главная роль отведена именно первому кольцу, которое расположено ближе к днищу. Этот путь является самым коротким к охлаждающей жидкости. Кольца являются прижатыми одновременно к поршневым канавками и к стенке цилиндра. Ими обеспечивается свыше половины теплового потока.
- Вторым путем является масло в двигателе. Именно оно имеет доступ к самым нагретым частям двигателя. В связи с этим, существенная часть тепла уносится масляным туманом в поддон картера.
- Третий путь поршневого охлаждения пролегает сквозь массивные бобышки в палец, после чего тепло попадает в шатун, после которого оно попадает в масло. Данный путь является менее интересным, поскольку во время его преодоления существуют еще тепловые сопротивления, такие как зазоры и стальные детали, которые обладают существенной длиной и низким коэффициентом теплопроводности.
- Четвертый путь заключается в том, что тепло забирает свежая топливовоздушная смесь, которая только что поступило в цилиндр.
Не смотря на такое, казалось бы, достаточное количество путей охлаждения поршня мотоцикла, все таки наиболее важным является отдача тепла посредством поршневых колец. Если этот путь перекрыть, то у двигателя не будет шансов выдержать большие нагрузки в течении длительного времени. Это приведет к значительному повышению температуры и расплавлению поршня, что, в свою очередь, разрушительно повлияет на двигатель.
Изменение неизменного. Продолжение. Начало в № 11/2017

Итак, мы остановились на том, что американская корпорация Continental на протяжении ряда лет выпускала дизель специального назначения AVCR-1100 с регулируемой высотой поршней. Степень сжатия в нем изменялась в пределах от 10 до 22. Увеличение высоты поршня от минимума до максимума происходило за 60–65 циклов или примерно за 3 с, потому что оно возможно лишь в течение небольшого периода времени, пока действующие на поршень силы инерции превышают силу противодавления газов. Низкое быстродействие – не самый значительный недостаток конструкций с телескопическими поршнями. Механизм с прецизионными элементами вынужден работать в условиях больших температур и нагрузок. Одно из вероятных следствий этого – коксование масла и потеря подвижности головки поршня. К тому же реализация способа связана с существенным увеличением массы поршней со всеми вытекающими последствиями.
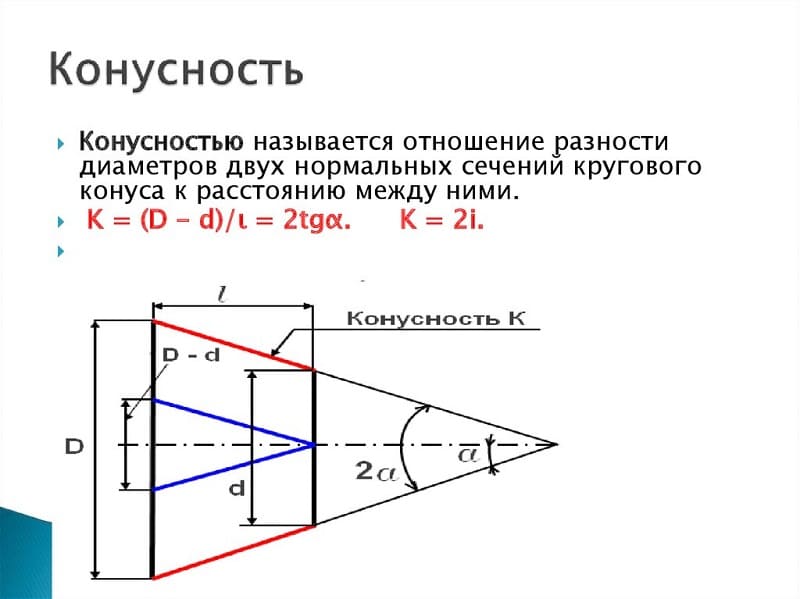
Формула для определения конусности
Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:
- K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
- Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
- F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.
Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.
На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.
Маятник Капицы
Обычный маятник, если перевернуть его кверху ногами, неустойчив. Для него крайне трудно найти верхнюю точку равновесия. Но если совершать быстрые вертикальные возвратно-поступательные колебания, то положение такого маятника становится устойчивым.
Петр Леонидович Капица
Советский академик и нобелевский лауреат по физике Петр Леонидович Капица (1894 — 1984) использовал модель маятника с вибрирующим подвесом для построения новой теории, которая описывала эффекты стабилизации тел или частиц. Работа Капицы по стабилизации маятника была опубликована в 1951 году, а сама модель получила название «маятник Капицы». Более того, было открыто новое направление в физике — вибрационная механика. Данная модель позволила наглядно показать возможности высокочастотной электромагнитной стабилизации пучка заряженных частиц в ускорителях.
Владимир Игоревич Арнольд
Другой советский математик и академик Владимир Игоревич Арнольд (1937-2010), который был заместителем Капицы, вспоминал его слова:
«Он (Капица — примечание) сказал: «Вот смотрите — когда придумывается какая-то физическая теория, то прежде всего надо сделать маленький какой-нибудь прибор, на котором его наглядно можно было-бы продемонстрировать кому угодно. Например, Будкер и Векслер хотят делать ускорители на очень сложной системе. Но я посмотрел, что уравнения, которые говорят об устойчивости этого пучка, означают, что если маятник перевернут кверху ногами, он обычно неустойчив, падает. Но если точка подвеса совершает быстрые вертикальные колебания, то он становится устойчивым. В то время как ускоритель стоит много миллионов, а этот маятник можно очень легко сделать. Я его сделал на базе швейной электрической машинки, он вот здесь стоит». Он нас отвел в соседнюю комнату и показал этот стоящий вертикально маятник на базе швейной машинки».
Демонстрация динамической стабилизации перевернутого маятника с помощью электробритвы
У математика Арнольда не было своей швейной машинки, и он огорчился. Но у него была электробритва «Нева», из которой и был собран перевернутый маятник. К сожалению, в первой конструкции маятник падал. Тогда Арнольд вывел формулу и увидел, что длина маятника не должна быть больше 12 сантиметров. Известный математик укоротил подвес до 11 сантиметров и все получилось.
Давайте посмотрим, какие силы действуют на «маятник Капицы». После прохождения верхней мертвой точки подвес маятника начинает тянуть грузик вниз. После прохождения нижней мертвой точки подвес толкает грузик вверх. Так как углы вежду векторами сил в верхней и нижней точке разные, то сумма их векторов дает силу, направленную к оси вертикальных колебаний маятника. Если эта сила больше силы тяжести, то верхнее положение маятника становится устойчивым.
А эта формула описывает взаимосвязь частоты вибраций подвеса, амплитуды колебаний и длины жесткого подвеса.
Видео:
- GetAClass. Маятник Капицы
- Маятник Капицы: диалог академика Арнольда и Капицы, вывод формулы
Решение задач
Задача 2 (Феденко №380)
Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=\mbox{sin}x$ в точке $A(\pi/2,1)$ общие касательную и кривизну.
Задача 3 (Феденко №405)
Составьте натуральные уравнения кривой: $$ x=a(\mbox{cos}\,t+t\,\mbox{sin}\,t), \,\, y=a(\mbox{sin}\,t-t\,\mbox{cos}\,t). $$
Краткое решение задачи 3
$$ s=\frac{at^2}{2}. $$
$$ k=\frac{1}{at}. $$
$$ t=\frac{1}{ak} \Rightarrow s= \frac{1}{2ak^2}. $$
Натуральные уравнения: $$ k=\frac{1}{at},\,\,s=\frac{at^2}{2} $$ или $$ k^2=\frac{1}{2as}. $$
Феденко записывает ответы через радиус кривизны: $R=\frac{1}{k}$.
Задача 4 (Феденко №486, №514)
Найдите кривизну и кручение, составьте натуральные уравнения кривой: $$ x=a\,\mbox{ch}t, \, y=a\,\mbox{sh}t, \, z=a\, t. $$
Решение задачи 4
Задачу можно решать двумя способами:
1 способ. Найти $k(t), \varkappa(t), s(t)$.
2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $\vec{r}=\vec{r}(s)$. А далее найти $k(s)$ и $\varkappa(s)$.
Воспользуемся первым способом. \begin{gather*} \vec{r}(t_0)=\{a\,\mbox{ch}t, \, a\,\mbox{sh}t, \, at\},\\ \vec{r’}(t_0)=\{a\,\mbox{sh}t, \, a\,\mbox{ch}t, \, a\},\\ \vec{r”}(t_0)=\{a\,\mbox{ch}t, \, a\,\mbox{sh}t, \, 0\}\\ \vec{r”’}(t_0)=\{a\,\mbox{sh}t, \, a\,\mbox{ch}t, \, 0\}. \end{gather*}
$$ \Rightarrow \quad k^2(t) = \frac{1}{4a^2\mbox{ch}^4t}. $$ $$ \Rightarrow \quad k(t) = \frac{1}{2a\,\mbox{ch}^2t}. $$
\begin{equation*} \varkappa(t) = \frac{ \left| \begin{array}{ccc} a\,\mbox{sh}t & a\,\mbox{ch}t & a \\ a\,\mbox{ch}t & a\,\mbox{sh}t & 0 \\ a\,\mbox{sh}t & a\,\mbox{ch}t & 0 \\ \end{array} \right|}{a^4\cdot 2\mbox{ch}^2t} = \frac{1}{2a\,\mbox{ch}^2t}. \end{equation*}
В задаче №473 была та же кривая и мы получили, что $$s=a\sqrt{2}\,\mbox{sh}\,t.$$ Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения: \begin{equation*} s=a\sqrt{2}\,\mbox{sh}t=a\sqrt{2}\,\sqrt{\mbox{ch}^2t-1} \,\, \Rightarrow \,\, \mbox{ch}^2t=\frac{s^2}{2a^2}+1 \,\, \Rightarrow \end{equation*} \begin{equation*} k(s)=\varkappa(s)=\frac{1}{2a\,\mbox{ch}^2t} = \frac{a}{s^2+2a^2}. \end{equation*}
Вычисления сделаны для $a>0$.
Задача 5 (Феденко №496)
Найдите функцию $f(t)$, для которой данная кривая — плоская: $$ \vec{r}(t)=\{a\,\mbox{cos}t, \, a\,\mbox{sin}t, \, f(t)\} $$
Решение задачи 5
$$ \begin{array}{lll} x=a\,\mbox{cos}t,\, &y=a\,\mbox{sin}t, \, &z=f(t),\\ x’=-a\,\mbox{sin}t, \, &y’=a\,\mbox{cos}t, \, &z’=f'(t),\\ x”=-a\,\mbox{cos}t, \, &y”=-a\,\mbox{sin}t, \, &z”=f”(t),\\ x”’=a\,\mbox{sin}t, \, &y”’=-a\,\mbox{cos}t, \, &z”’=f”'(t). \end{array} $$
Для плоской кривой кручение равно нулю: \begin{equation*} \varkappa(t) = \left| \begin{array}{rrr} -a\,\mbox{sin}t & a\,\mbox{cos}t & f'(t) \\ -a\,\mbox{cos}t & -a\,\mbox{sin}t & f”(t) \\ a\,\mbox{sin}t & -a\,\mbox{cos}t & f”'(t) \\ \end{array} \right| = \left( f'(t) + f”'(t) \right)\cdot2a^2=0. \end{equation*} \begin{equation*} f'(t)=-f”'(t) \quad \Rightarrow \quad f(t)=c_1+c_2\,\mbox{sin}t+c_3\,\mbox{cos}t. \end{equation*}
Как найти уравнение плоскости, в которой лежит кривая?
Известно, что плоская кривая лежит в своей соприкасающейся плоскости! Второй способ — составить уравнение плоскости по трем точкам.
Применение нетрадиционных преобразующих механизмов
Данное направление работ по созданию VCR-двигателя без натяжки можно назвать популярным. Им занимались и продолжают интенсивно заниматься многие автоконцерны – Ford, Mercedes-Benz, Nissan, Peugeot/Citroёn – и моторные исследовательские компании: немецкая FEV Motorentechnik, британская Mayflower и французская MCE-5 Development. На протяжении многих лет аналогичные разработки ведутся и в НАМИ. Попробуем понять причину интереса к этой тематике.
Полистав увесистый томик ТММ (теория механизмов и машин, на студенческом сленге – тут моя могила), можно обнаружить огромное количество кинематических схем механизмов, которые, в принципе, возможно использовать в ДВС для передачи движения от поршня к коленчатому валу. Кривошипно-шатунный механизм – простейший из них, в чем состоит его неоспоримое достоинство. В соответствии с классификацией КШМ является одноэлементным преобразующим механизмом, поскольку поршень связан с кривошипом единственным звеном – шатуном
Внимание двигателистов привлекли трехэлементные механизмы, которые при относительной простоте потенциально способны обеспечить важное преимущество – гибкое управление движением поршня. Трехэлементные устройства подразделяют на две большие группы – балансирные и траверсные. В первых связанное с шатуном звено (балансир) вращается, во вторых оно совершает сложное плоское движение и называется траверсой
В первых связанное с шатуном звено (балансир) вращается, во вторых оно совершает сложное плоское движение и называется траверсой
В первых связанное с шатуном звено (балансир) вращается, во вторых оно совершает сложное плоское движение и называется траверсой
Балансирные механизмы соединяются с кривошипом тягой, траверсные – самой траверсой
В первых связанное с шатуном звено (балансир) вращается, во вторых оно совершает сложное плоское движение и называется траверсой. Балансирные механизмы соединяются с кривошипом тягой, траверсные – самой траверсой.
Было запатентовано и экспериментально отработано множество конструкций балансирных ДВС. Большинство из них представляли собой 2-тактные двигатели с противоположным движением поршней. Исследования показали, что ставка на балансирные механизмы себя не оправдывает. Хотя балансирные двигатели демонстрировали достаточно высокую надежность, они имели значительно большие габариты по сравнению с традиционными, ненамного превосходя их по возможности регулирования движения поршней. Гораздо более обнадеживающие результаты были получены в ходе экспериментальной отработки траверсных механизмов. Было доказано, что при определенных условиях они способны обеспечить следующие преимущества:
- приемлемый диапазон регулирования степени сжатия (ε = 7–15);
- возможность одновременного регулирования степени сжатия и рабочего объема, причем по оптимальному алгоритму;
- возможность сведения к минимуму дисбаланса двигателя за счет оптимизации закона перемещения поршней и использования массы дополнительных элементов;
- небольшие нагрузки на органы управления VCR-механизмом и, как следствие, достаточно высокое быстродействие;
- отсутствие экзотических деталей, использование традиционных для двигателестроения технологий.
Именно поэтому траверсный механизм взят за основу большинством из упомянутых выше разработчиков VCR-двигателей. Это не означает, что все они движутся «след в след». Используются разные кинематические схемы и различные конструктивные решения. Выражение «при определенных условиях» было употреблено ранее неслучайно. Действительно, преимущества траверсных механизмов присущи им отнюдь не «по определению». Они достигаются только тогда, когда геометрические и конструктивные параметры всех звеньев оптимизированы с точки зрения закона движения поршня, уравновешенности механизма и прочности. На текущем этапе эти вопросы являются основным предметом исследования. Помимо этого отрабатываются различные варианты привода механизма и алгоритма автоматического управления степенью сжатия.
Тем временем фирма MCE-5 ведет работы в другом направлении. В предложенной ею конструкции VCR-двигателя используется КШМ, но нетрадиционным способом. Верхняя головка шатуна соединена не с поршнем, а с осью зубчатого колеса, которое, в свою очередь, связано со штангой, жестко прикрепленной к поршню. Решение на первый взгляд не бесспорное, но, по заявлениям разработчиков, обладающее рядом достоинств. Утверждается, что механизм позволяет регулировать степень сжатия в широких пределах, обеспечивает минимальные потери на трение ввиду отсутствия бокового давления поршня на стенки цилиндра, исключительно надежен и имеет большой ресурс.
Введите значения H и h в миллиметрах
Не забывайте, что для гибки профилей необходим технологический припуск от 500 до 1000 мм. на заготовку.
Вы можете скачать ПК версию гибочного калькулятора по этой ссылке.
140030, МО, Люберецкий район, пос. Малаховка, Касимовское шоссе, д. 3Г
Право собственности ООО «ПК РАДИУС» 2002–2017. Все права защищены.
Калькулятор рассчитывает глубину прогиба профиля трубогибом или гибочным станком для получения заданных параметров.
Статья написана в ответ на запрос пользователя, который хотел вычислять глубину прогиба профиля ведущим валом, для получения изогнутой трубы с заданными параметрами. До запроса я даже и не знал, что есть специальные машины для холодной гибки труб. Причем бывают как и промышленные гибочные станки, так и ручные гидравлические трубогибы.
Все они действуют по одному принципу, который можно понять, посмотрев на картинку.
Профиль (труба) укладывается между валиками, затем центральный валик с усилием прогибает профиль, и дальше оставшийся кусок прокатывается через станок.
С моей дилетантской точки зрения, процесс выглядит примерно так
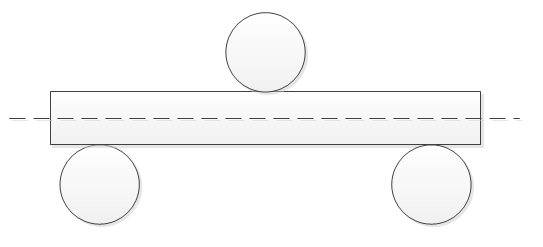
Или, если совместить:
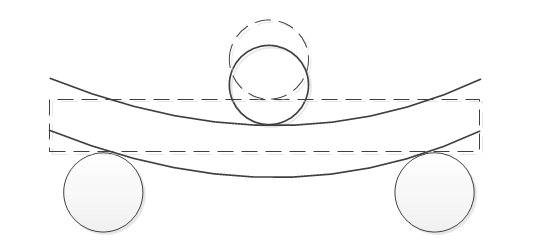
Собственно, интересует вопрос — насколько надо прогнуть трубу, то есть опустить ведущий вал, чтобы после прокатки всего отрезка профиля получить заданный изгиб? Изгиб трубы, очевидно, задается радиусом. Но, как показал запрос пользователя, параметры могут быть заданы не только радиусом, но и длиной и высотой хорды, если надо получить арку. Здесь нам пригодится калькулятор, который по заданной длине (C) и высоте хорды (h) рассчитывает длину требуемого отрезка (L) и радиус окружности (R) — смотри рисунок.
Параметры сегмента по хорде и высоте
Подробности и формулы смотри здесь — Сегмент круга
Идем дальше. Итак, нам нужно получить глубину прогиба зная радиус, расстояние между ведомыми валиками, радиус валиков и размеры профиля. Перерисуем совмещенный рисунок, добавив несколько нужных линий, и убрав все ненужные.
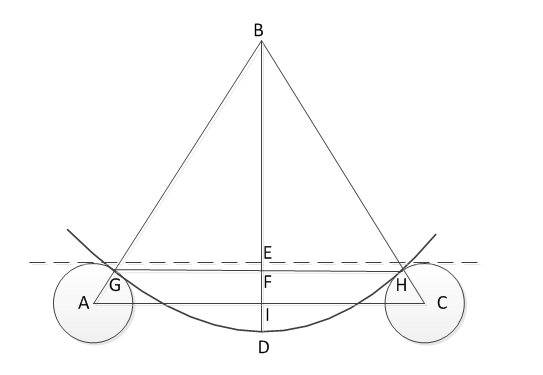
Точка B — центр нашей окружности
Обратите внимание, что расчет идет по внешнему по отношению к изгибу краю профиля. Поскольку радиус по высоте и ширине хорды скорее всего будет рассчитываться по оси профиля, к полученному радиусу надо прибавить радиус профиля так, чтобы получить радиус внешнего края профиля. Дальше в ход идет геометрия
Из расстояния AC и расстояния AB находим угол ABD
Дальше в ход идет геометрия. Из расстояния AC и расстояния AB находим угол ABD.
При монтаже трубопроводов из различного вида материалов его изгиб позволяет уменьшить количество разборных или сварных соединений, понижающих надежность магистрали. При проведении трубогибочных работ полезно знать допустимый радиус гиба трубы, обеспечивающий безопасность и надежную эксплуатацию трубопроводной системы в соответствии с технической документацией.
Чаще всего изгибаемые трубы выполнены из стали и коррозионно-стойких металлов: нержавейки, меди, алюминия, латуни, при устройстве бытовых систем отопления и водопроводов изгибают изделия из пластика и металлопластика. Методы сгибания труб по радиусу различны в зависимости от материала их изготовления и могут быть выполнены ручным или электромеханическим способом на специальных станках.
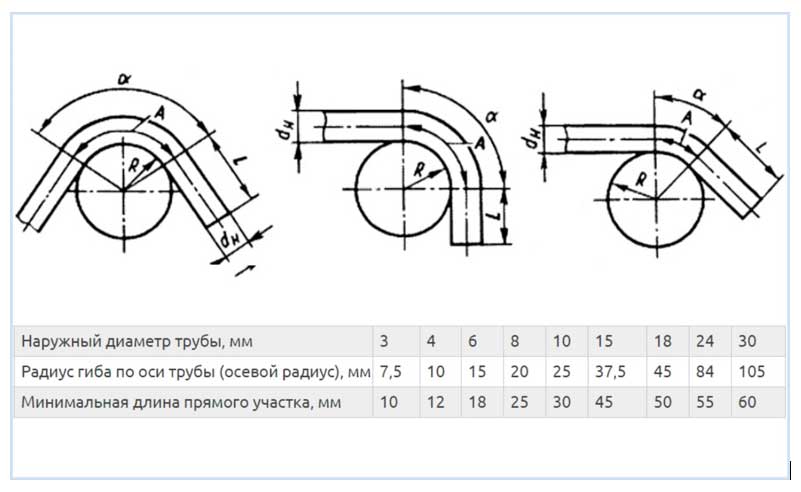
Рис. 1 Углы гиба медных труб и изделий из латуни
Виды кулисных механизмов
В исходя из типа подвижного звена рычажной схемы в установках и подвижных узлах используются следующие виды кулисных пар:
- Ползунный. Система рычагов, состоящая из четырех звеньев. Основные части- это кулиса и ползун с зафиксированной направляющей. Она дает ползуну единственную степень свободы, для совершения линейных перемещений. Качания кулисы превращаются устройством в линейное перемещение ползуна. Кинематическая схема обратима- возможно и обратное преобразование движения.
- Кривошипный. Кривошипно-кулисного механизм построен по четырехрычажной кинематической схеме. Передает вращение кривошипа кулисе, также вращающейся или качающейся. Распространен в промышленных установках, например — в продольно-долбежных и строгальных. Для них применяют кривошипно-коромысловый механизм c вращающейся кулисой. Такая схема обеспечивает очень высокую скорость прямого ходя и медленный возврат. Применяется также в установках для упаковки.
- Двухкулисный. В кинематической четырехзвенной схеме есть пара кулис. Передается вращение или качание через промежуточный рычаг. Передаточное число неизменно и всегда составляет единицу. Применяется в компенсирующих муфтах.
- Коромысловый. Состоит из коромысла, кулисы и связывающего их шатуна. Позволяет располагать оси симметрии зон движения, ведущего и ведомого звеньев под углом около 60°. Находит применение в автоматизированных производственных линиях
Реже находит применение в транспортных средствах и некоторых измерительных приборах стоящий несколько особняком прямолинейно- направляющий или конхоидальный механизм.
Понятия и нормы
Полиэтилен относится к достаточно прочным и одновременно пластичным структурам, что позволяет нагревать его до размягченного состояния и придавать изделиям требуемую форму. При грамотно организованном процессе формовки критических нарушений структуры материала, как правило, не наблюдается.
Указанные свойства допускают применение заготовок из полиэтилена при монтаже трубопроводов, так как в этом случае можно легко огибать препятствия или менять направление предполагаемой прокладки. Под минимальным радиусом изгиба типовой полиэтиленовой трубы понимается предельный показатель, при котором она сохраняет свою стойкость и не ломается.
Радиус изгиба
Этот параметр, выражаемый в метрических единицах, зависит от следующих факторов:
- Температуры стенок трубного изделия.
- Технические параметры, относящиеся к его геометрическим пропорциям.
Под последними понимается показатель SDR, представляющий собой соотношение наружного диаметра трубной заготовки к заявленной толщине ее стенок.
При вычислении безопасного для эксплуатации показателя изгиба следует придерживаться именно этих исходных данных (SDR и температура материала или окружающей среды).
Описание и терминология
График ссылок {*}
Система шатун-кривошип позволяет преобразовать линейное движение конца шатуна в непрерывное вращательное движение, доступное для кривошипа ( коленчатого вала ), и наоборот. Он состоит из 4 основных частей:
- рамы (1).
- кривошипа (2), также называемый коленчатый вал на двигателях,
- соединительный стержень (3),
- Эффектор (4): поршень , рычаг, педали в зависимости от случая,
Система обычно дополняется маховиком, стабилизирующим скорость вращения кривошипа.
Паровая машина, шток соединен с поршнем по прямолинейной траектории.
Движение на половину вращения, звено соединено с другим кривошипом
Кривошип и исполнительный элемент составляют две входные-выходные части механизма.
Кривошип (приводной или принимающий) приводится в движение непрерывным вращательным движением , в то время как исполнительный элемент приводится в движение переменным линейным движением, прямолинейным или нет. Шатун имеет два сочленения: с одной стороны на кривошип, а с другой – на эффектор. В зависимости от типа соединения, наложенного на эффектор, система выполняет следующие преобразования движения:
Непрерывное вращение возвратно-поступательное прямолинейное движение.⇔{\ displaystyle \ Leftrightarrow}
Это тот случай, когда конец шатуна прикреплен к поршню, подвижному в цилиндре, или, в более общем смысле, к скользящему соединению. Конец шатуна описывает прямой отрезок. Примеры:
- направление двигателя : тепловая машина, паровая машина.
- Направление приема : гидростатический насос, компрессор, пильный станок, швейная машина (движение иглы), перфоратор.
Непрерывное вращение переменное вращение.⇔{\ displaystyle \ Leftrightarrow}
Это тот случай, когда конец шатуна соединен с другим кривошипом, педалью или шарнирным рычагом. Конец шатуна описывает круговой сегмент кривой. Примеры:
- направление мотора : педальное устройство, детская коляска, швейная машинка (тренировочная), прялка.
- направление приемника : альтернативный роторный насос, стеклоочиститель, автоматический шлагбаум, транспортер.
и вообще любой четырехстворчатый механизм
Устройство автомобиля
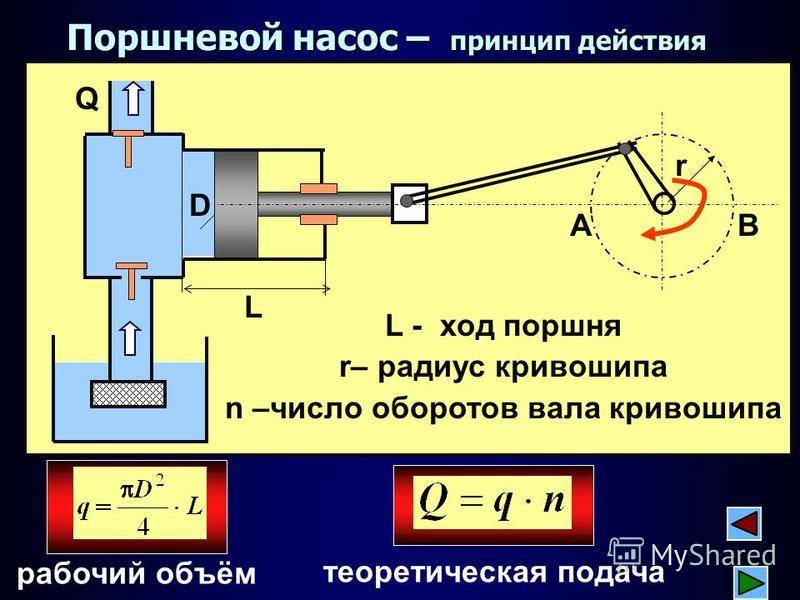
Поршневой двигатель внутреннего сгорания состоит из следующих механизмов и систем:
- кривошипно-шатунный механизм (КШМ);
- газораспределительный механизм (ГРМ);
- система охлаждения;
- смазочная система;
- система питания;
- система зажигания (в карбюраторном двигателе);
- система электрического пуска двигателя.
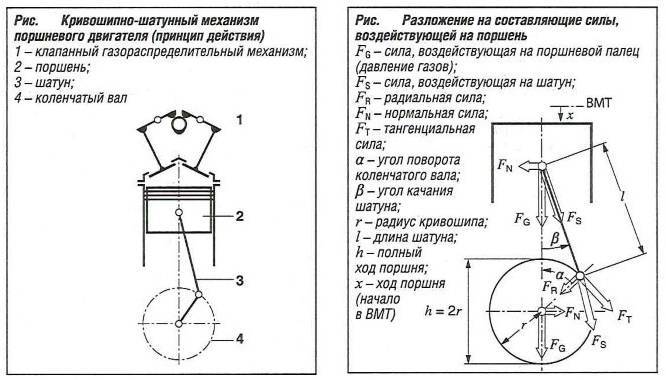
В поршневом ДВС (рис. 1) преобразование энергии происходит в замкнутом объеме, который образован цилиндром, крышкой (головкой) цилиндра и поршнем. В карбюраторном двигателе горючая смесь вводится в цилиндр через впускной клапан, смешиваясь с остатками отработавших газов — образует рабочую смесь, которая сжимается поршнем и воспламеняется. Образовавшиеся при сгорании газы перемещают поршень, который через шатун передает усилие на кривошип коленчатого вала, поворачивая его вокруг оси. Отработавшие газы вытесняются при обратном движении поршня через выпускной клапан. Таким образом, тепловая энергия преобразуется в механическую, а возвратно-поступательное движение — во вращательное как наиболее удобный для трансформации вид движения.
Рис. 1. Схема четырехтактного одноцилиндрового карбюраторного двигателя: 1 — распределительный вал; 2 — толкатель; 3 — цилиндр; 4 — поршень; 5 — штанга; 6 — впускной клапан; 7 — коромысло; 8 — свеча зажигания; 9 — выпускной клапан; 10 — поршневые кольца; 11 — шатун; 12 — коленчатый вал; 13 — поддон
При вращении коленчатого вала поршень дважды за один оборот останавливается и меняет направление движения.
Основные параметры двигателей
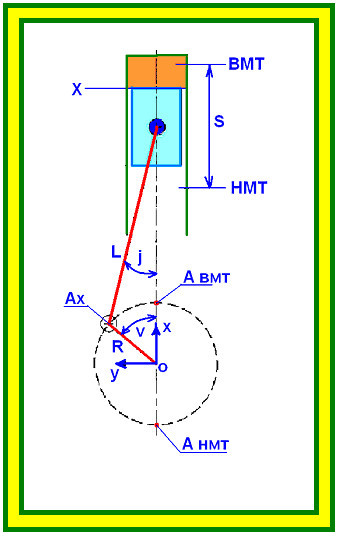
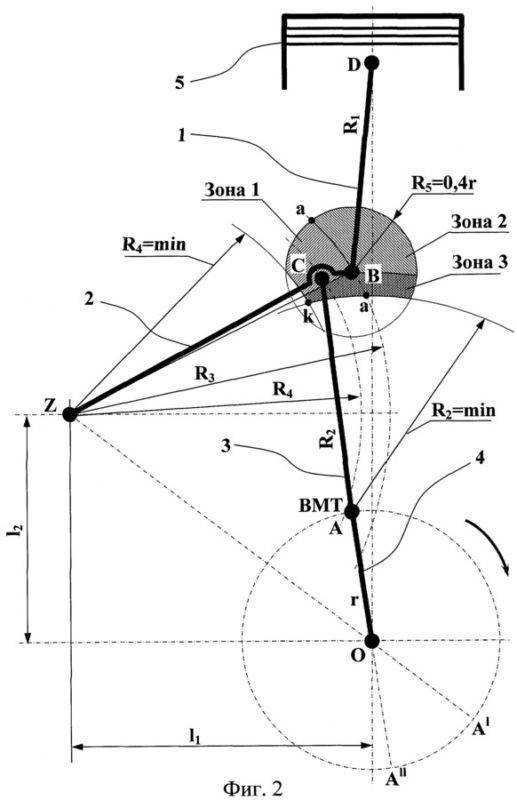
Верхняя мертвая точка (ВМТ) — крайнее верхнее положение поршня (рис. 2).
Нижняя мертвая точка (НМТ) — крайнее нижнее положение поршня. Радиус кривошипа — расстояние от оси коренной шейки коленчатого вала до оси его шатунной шейки.
Ход поршня S — расстояние между крайними положениями поршня, равное удвоенному радиусу кривошипа коленчатого вала. Каждому ходу поршня соответствует поворот коленчатого вала на угол 180° (пол-оборота).
Рис. 2. Основные положения кривошипно-шатунного механизма: а — ВМТ; б — НМТ; Vc — объем камеры сгорания; Vh — рабочий объем цилиндра; D — диаметр цилиндра; S — ход поршня
Ход поршня S и диаметр D цилиндра обычно определяют размеры двигателя.
Такт — часть рабочего цикла, происходящая за один ход поршня.
Объем камеры сгорания — объем пространства над поршнем при его положении в ВМТ.
Рабочий объем цилиндра объем пространства, освобождаемого поршнем при перемещении его от ВМТ к НМТ.
Полный объем цилиндра — объем пространства над поршнем при нахождении его в НМТ. Очевидно, что полный объем цилиндра равен сумме рабочего объема цилиндра и объема камеры сгорания.
Степень сжатия ε — отношение полного объема цилиндра к объему камеры сгорания.
Индикаторная мощность Ni, мощность, развиваемая газами в цилиндре.
Эффективная (действительная) мощность Ne — мощность, развиваемая на коленчатом валу двигателя. Эффективная мощность Ne меньше индикаторной Ni, так как часть последней затрачивается на трение и на приведение в движение вспомогательных механизмов. Эта мощность называется мощностью механических потерь Nм.
Механический КПД (коэффициент полезного действия) двигателя ηм — отношение эффективной мощности к индикаторной:
Индикаторный КПД ηi, представляет собой отношение теплоты Qi эквивалентной индикаторной работе, ко всей теплоте Q, введенной в двигатель с топливом.
Эффективный КПД ηе — отношение количества теплоты Q2, превращенного в механическую работу на валу двигателя, ко всему количеству теплоты Q1, подведенному в процессе работы.
Среднее эффективное давление ре — произведение среднего индикаторного давления рi (давление, действующее на поршень в течение одного хода поршня) на механический КПД ηм.
Удельный индикаторный расход топлива qi — количество топлива, расходуемого в двигателе для получения в течение 1 ч индикаторной мощности 1 кВт.
Удельный эффективный расход топлива ge — количество топлива, которое расходуется в двигателе для получения в течение 1 ч 1 кВт эффективной мощности.
Расчет минимального диаметра при заданной длине
Для приблизительных расчетов радиуса изгиба потребуются две жесткие линейки 30 и 50-сантиметровой длины (их выбор зависит от величины изгиба). Порядок действий выглядит так:
- Сначала замеряется радиус сгиба уже сформованной трубы, который нужно скопировать на исходную заготовку.
- При измерении сильного загиба берется линейка на 30 см и прикладывается к концам изогнутой трубы, после чего замеряется расстояние между ней и серединой заготовки.
- При малом изгибе (большей длине трубы) эти же операции проделываются с линейкой на 50 см, как это показано на приведенном ниже фото.
Снятие данных для расчета А – интервал (просвет), мм.
D – диаметр дуги, мм.
R – радиус, на который предполагается загнуть трубу, мм.
Для понимания, что такое искомый параметр R следует ориентироваться на фото ниже по тексту, где приведен образец уже загнутой заготовки.
Исходя из полученных при измерениях данных, далее нужно подобрать подходящий по величине показатель радиуса (диаметра) дуги, значения которых можно найти в специально подготовленных таблицах. Они размещены в источниках в интернете (где учтены различные варианты предварительных измерений).
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
- Если в точке пересечения радиуса с поверхностью окружности провести касательную, то эти две линии будут пересекаться под прямым углом. Доказательство этой теоремы наглядно приводится на следующем рисунке.
Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
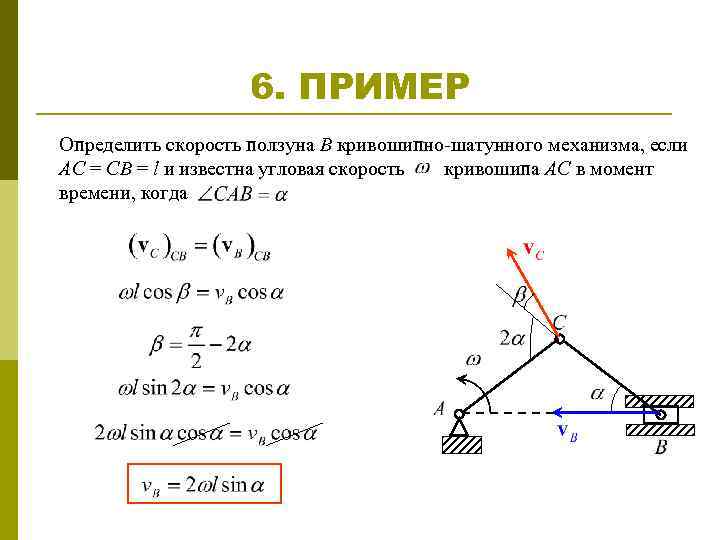
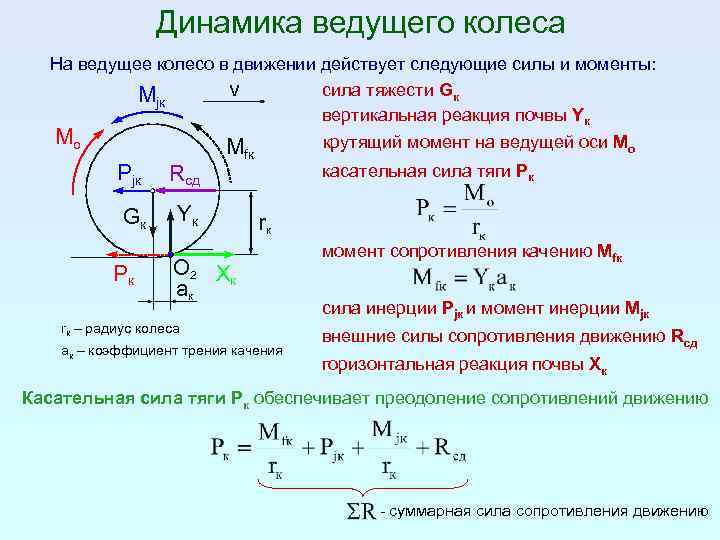
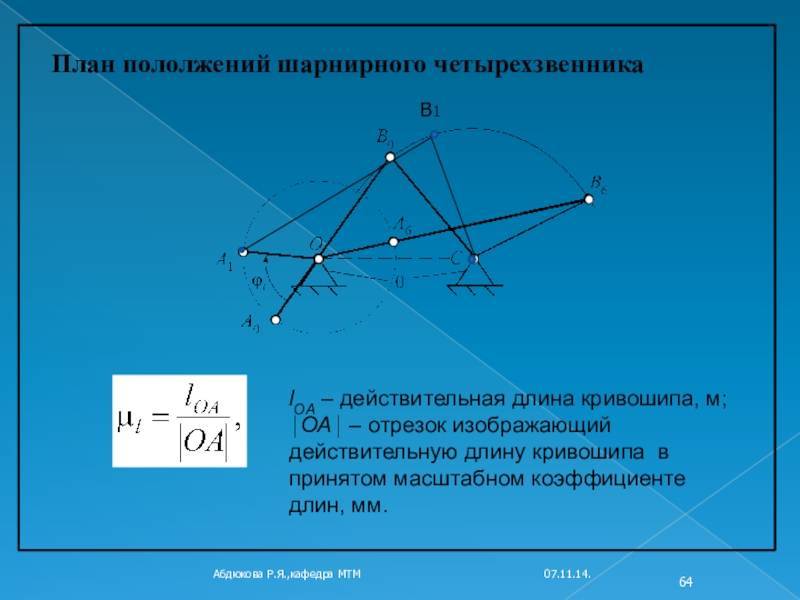
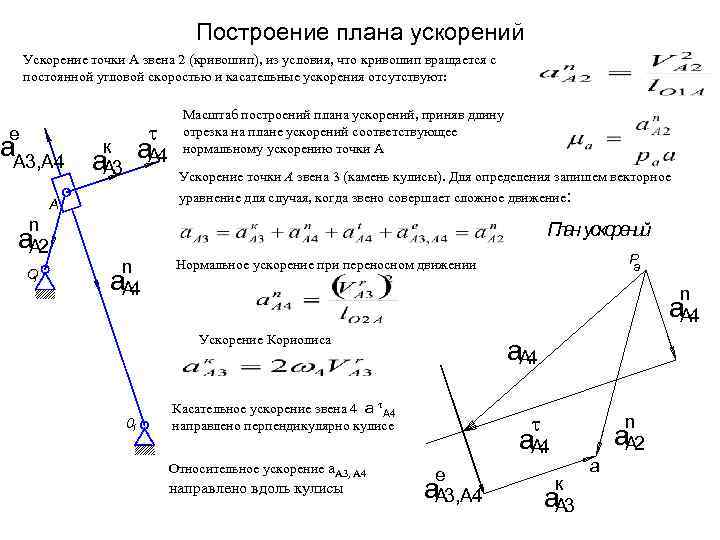
Расчеты механизмов
1 Расчеты рычажных механизмов
В результате проведения расчетов рычажного механизма необходимо определить размеры и взаимное расположение его звеньев, их кинематические параметры (скорость, ускорение), крутящий момент, приведенный к ведущему звену (кривошипному валу) обеспечивающий его работу в требуемом режиме и геометрические размеры его звеньев, позволяющие передавать возникающие при работе механизма усилия.
Методика выполнения кинематических и силовых расчетов рычажного механизма зависит от его типа, а прочностной расчет геометрических размеров входящих в него звеньев – от их конструктивного исполнения и направления сил и моментов, действующих на них. В общем, случае расчет рычажного механизма выполняется в следующей последовательности:
- расчет размеров (длин), определение исходного и конечного положения звеньев механизма, а также величину перемещения и траекторию движения его выходного звена,
- расчет скоростей и ускорений, возникающих в звеньях механизма,
- расчет усилий, в том числе инерционных, действующих на звенья механизма и потребного крутящего момента приведенного к ведущему звену,
- прочностной расчет звеньев механизма, (коленвал, шатун, ползун, шарниры),
- прочие расчеты, определяемые спецификой конструкции и работы механизма.