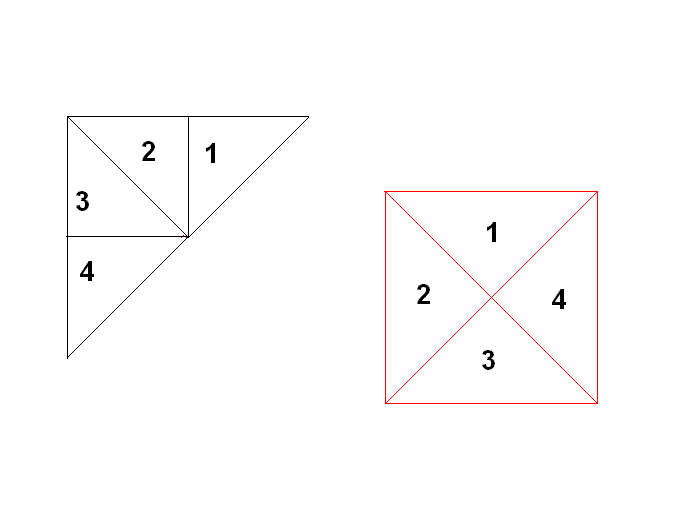
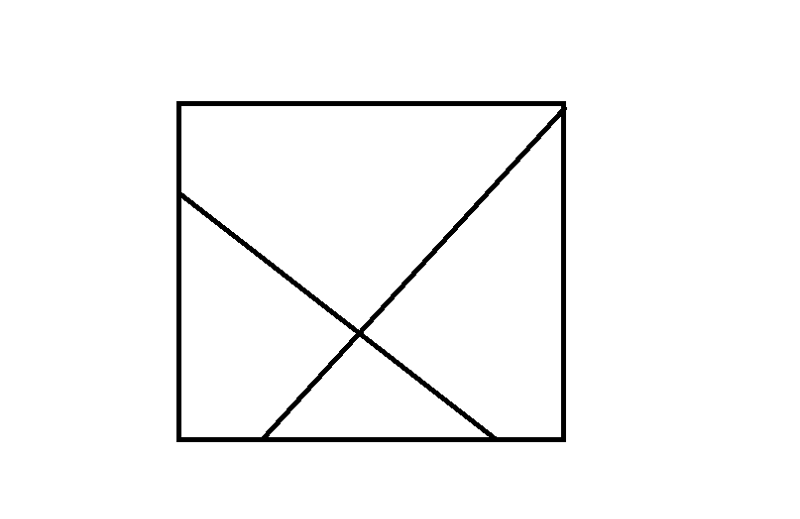
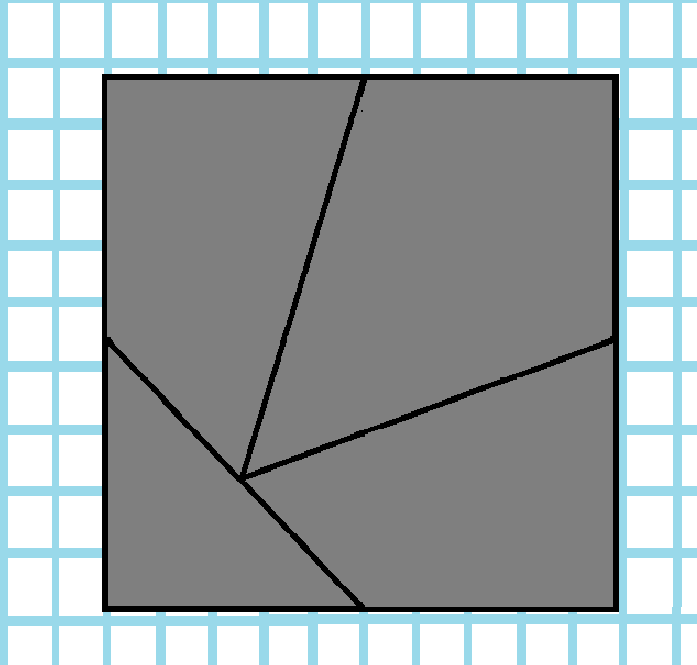
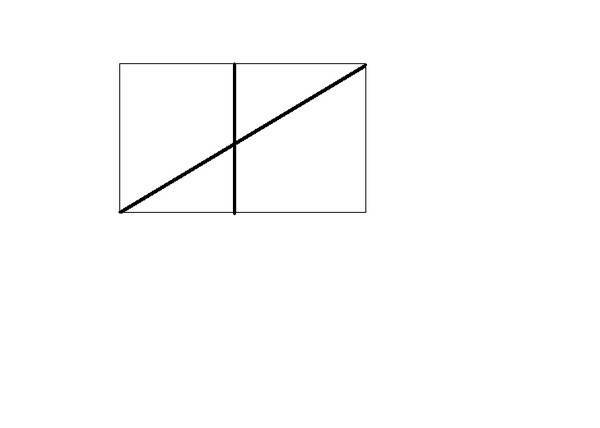
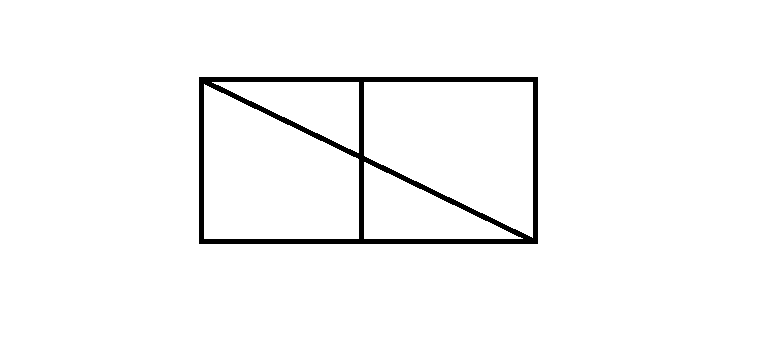
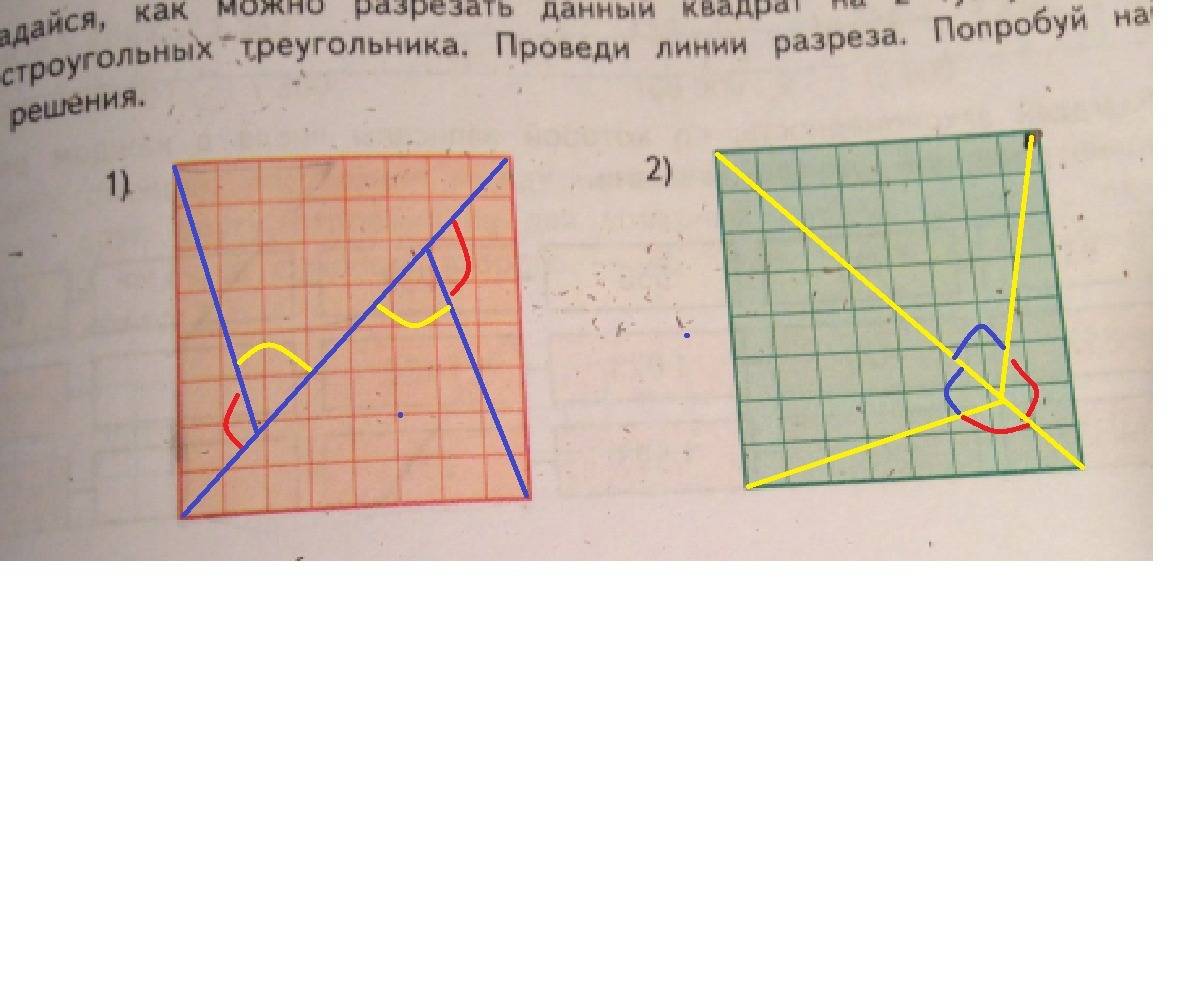
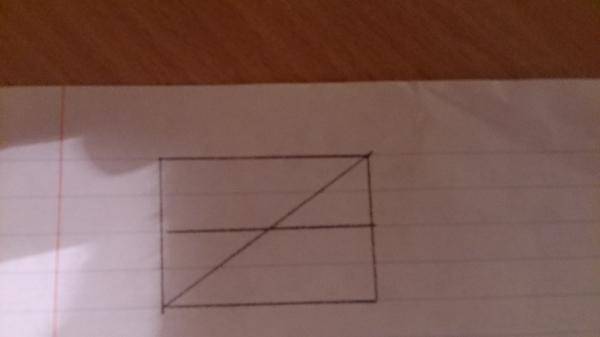
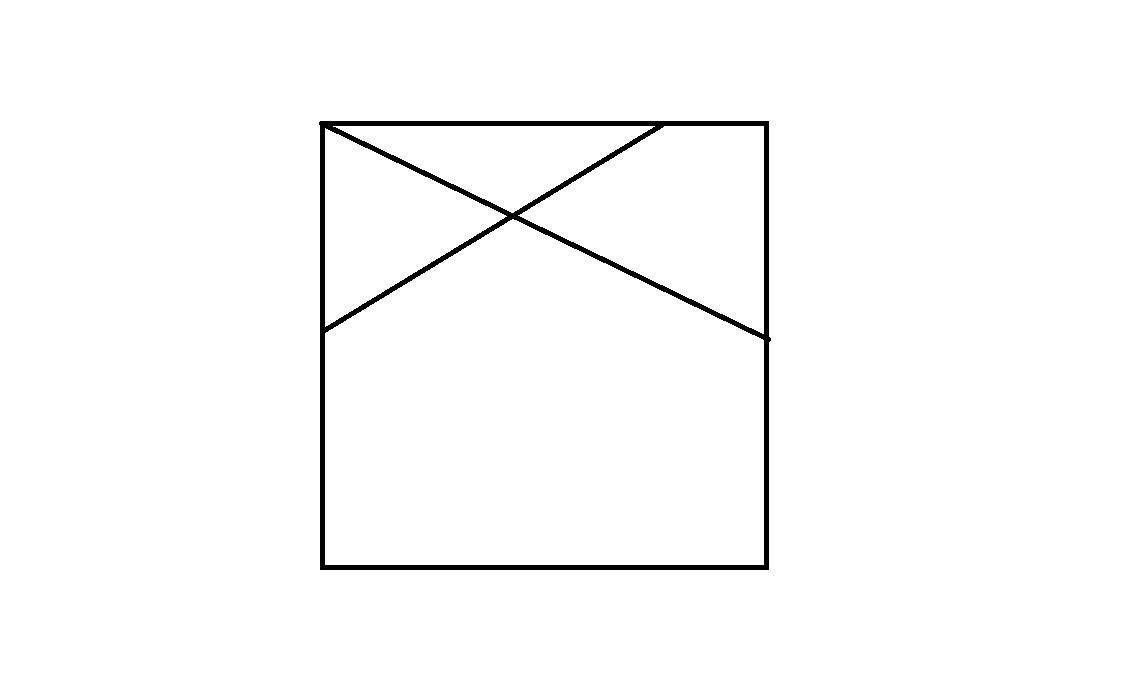
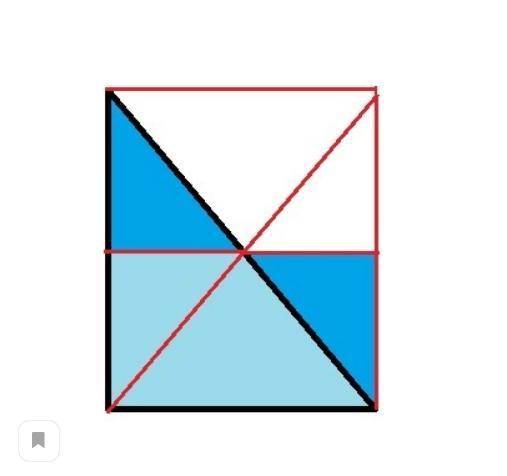
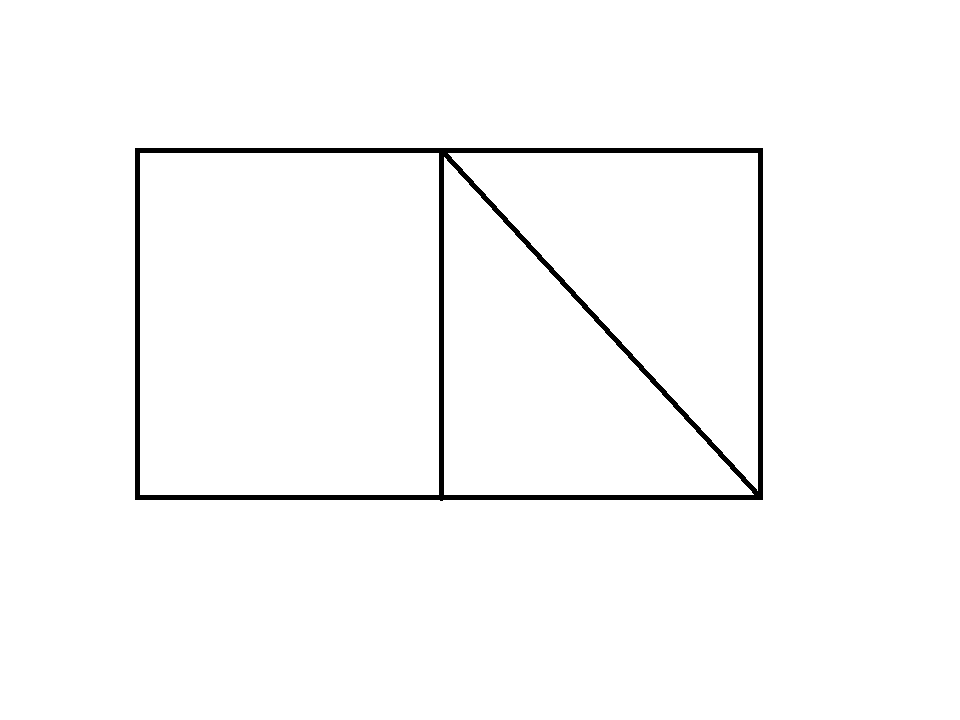
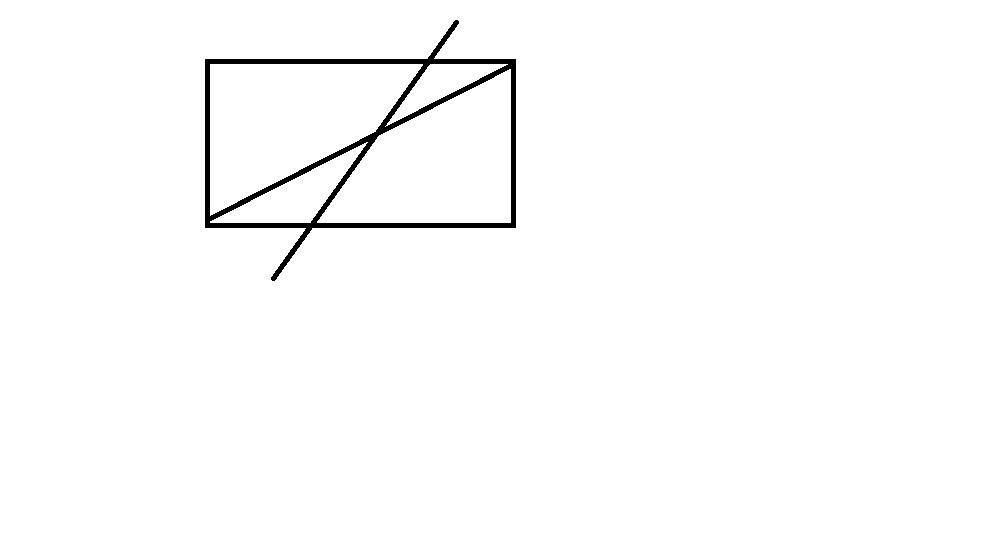
Раздели квадрат двумя линиями на 2 треугольника и 2 четырёхугольника?
Раздели квадрат двумя линиями на 2 треугольника и 2 четырёхугольника.
Вы перешли к вопросу Раздели квадрат 2 линиями на 2 треугольника и 2 четырёхугольника?. Он относится к категории Математика, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Свет проходит это расстояние за 20 лет, а космический аппарат в 100 раз дольше или 20 * 100 = 2 000 лет — ОТВЕТ.
Да можно но с ветром будет тяжело котаться.
Да ветер подталкивать будет.
1 1 / 5×6 1 / 3÷1 2 / 6 = 6 / 5×19 / 3÷8 / 6 = 38 / 5×6 / 8 = 114 / 20 = 5 14 / 20 = 5 7 / 10.
1) 72 : 8 = 9 2) 73 : 8 = 9 (ост 1) 3) 74 : 8 = 9 (ост2) 4) 63 : 7 = 9 5) 64 : 7 = 9 (ост1) 6) 65 : 7 = 9(ост 2).
73 / 8 = 9 1 / 8 74 / 8 = 9 2 / 8 64 / 7 = 9 1 / 7 65 / 7 = 9 2 / 7.
А) 8615, 8165, 6815, 6185, 1865, 1685 б) 3470, 3740, 4370, 4730, 7340, 7430.
123, 132, 213, 231, 312, 321 всего 6 чисел.
Различными размещениями из трех элементов по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком. Число размещений в комбинаторике обозначается Anmи ..
0, 3 + 3х ^ 2 = 0 3х ^ 2 = — 0, 3 х ^ 2 = — 0, 1 Корней нет, поскольку квадрат числа не может быть меньше ноля. Ответ : корней нет.
Решение задачи про треугольник
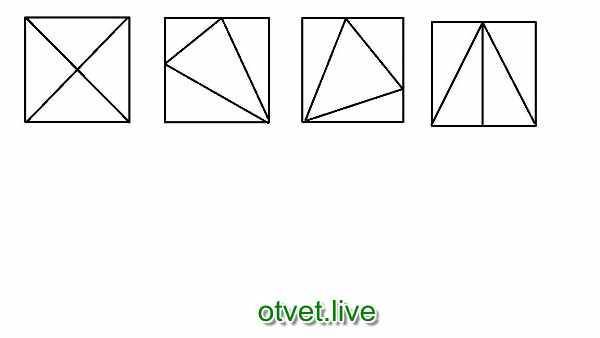
Для того, чтобы разрезать треугольник двумя разрезами на три четырехугольника и 1 треугольник нужно понять, что мы не можем разрезать треугольник лучами, исходящими из его вершин, потому что тогда для четырехугольников вершин будет недостаточно. Четырехугольники образованы двумя лучами, значит, каждые две стороны должны быть у них общими с соседними четырехугольниками. Таким образом общими будут 5 вершин. И три вершины — вершины треугольника. Всего получится 8 точек пересечения, одна из которых внутри треугольника, четыре на его сторонах и три — вершины треугольника. Таким образом, нарисовать такой способ разрезания треугольника двумя разрезами можно так:
Разрезать треугольник можно так
Или разрезать треугольник можно так
Или еще так можно разрезать треугольник
Главное, чтобы лучи не выходили из вершин, а давали нам дополнительные вершины для четыреухгольников. Для этого они должны пересекать стороны треугольника.
Любая из этих трех картинок — правильная. И можно нарисовать множество вариаций.
Превращения квадрата
В умелых руках любознательного человека самый обыкновенный, хорошо всем знакомый квадрат становится удивительной геометрической фигурой.
Он может, например весь без остатка превратиться в другую фигуру или в несколько других фигур правильной или неправильной формы. Но для каждого превращения квадрат предварительно должен быть разрезан на определенные части.
Очень остроумно разрезал квадрат еще несколько тысяч лет назад китайский ученый Та-нг.
Вероятно, эти части квадрата первоначально служили для демонстрации геометрических фигур. В самом деле, из частей данного квадрата легко можно составить прямоугольник, параллелограмм, трапецию.
С течением времени было замечено, что из этих частей можно составить множество фигур-силуэтов самой причудливой формы, употребляя для составления каждой фигуры все семь частей квадрата. Так создалась увлекательная игра головоломка. получившая широкое распространение, в особенности на своей родине. в Китае. Там эта игра известна так широко, как, например, у нас шахматы. Устраиваются даже специальные состязания на составление наибольшего количества фигур с наименьшей затратой времени. Победители получают специальные призы.
Меня заинтересовала эта идея, и я тоже попробовал создать различные картинки. силуэты из предложенных частей квадрата. Так состоялось мое первое знакомство с превращением квадрата. (Приложение)
Однажды мне на глаза попалась головоломка, где из семи частей квадрата предлагалось составить три одинаковых квадрата.
Квадрат из головоломки очень похож на механизм с хорошо прилаженными частями, которые можно разобрать и из тех же частей собрать новый механизм. Дл того. Чтобы из готовых частей квадрата составить указанные геометрические фигуры, не нужны какие. либо расчеты и построения, достаточно проявить настойчивость, терпение, смекалку и решение находится.
Складывая фигуры из частей данной головоломки, я увидел, что можно получить не только три одинаковых квадрата, но и прямоугольник, составленный из этих квадратов.
Однако, для тех, кто увлечен математикой, не достаточно только складывать многоугольники из готовых частей квадрата, а хочется самому научиться разрезать квадрат на части, необходимые для составления той или иной фигуры. Иными словами. дать обоснование возможности превращения фигур. На языке геометрии это значит: найти те геометрические построения, при помощи которых разрезается квадрат, и доказать, что из полученных частей может быть составлена требуемая фигура. Такая постановка вопроса сразу превращает нашу головоломку в более интересную, но и более трудную геометрическую задачу на фигур.
Сформулируем задание головоломки как геометрическую задачу:
Показать, каким образом нужно разделить данный квадрат прямоугольными разрезами, чтобы переложением полученных частей можно было составить три сплошных квадрата, равных между собой.
Здесь ничего не сказано о том, на сколько частей можно резать данный квадрат, а значит можно получить различные решения одной и той же задачи на перекраивание фигуры. Таким образом, при решении подобного рода задач открывается широкая возможность проявления геометрической интуиции.
Познакомимся с тем решением, которое дал Абул Вефа. Он разрезал квадраты 1 и 2 по диагоналям и каждую из половинок приложил к квадрату 3, как показано на рисунке.
Разрежьте правильно на части
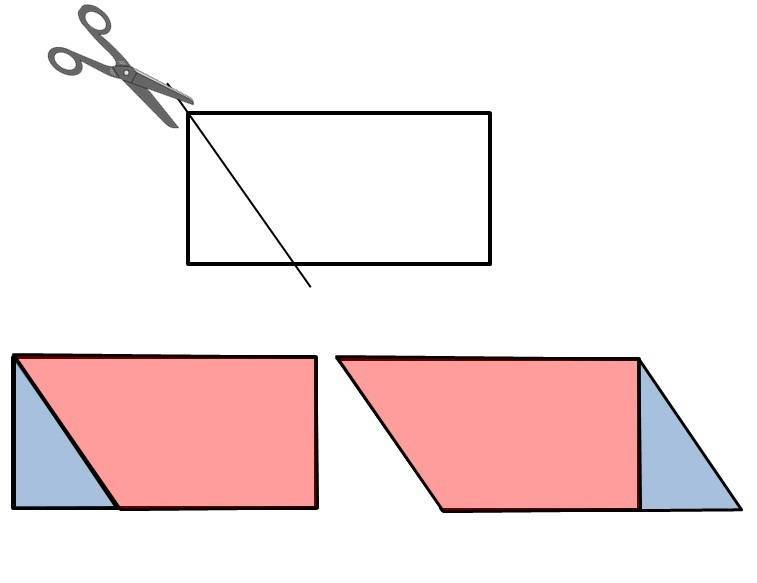
729. Как данный прямоугольник следует разрезать на две такие части, чтобы из них можно было сложить: 1) треугольник, 2) параллелограмм (отличный от прямоугольника), 3) трапецию?
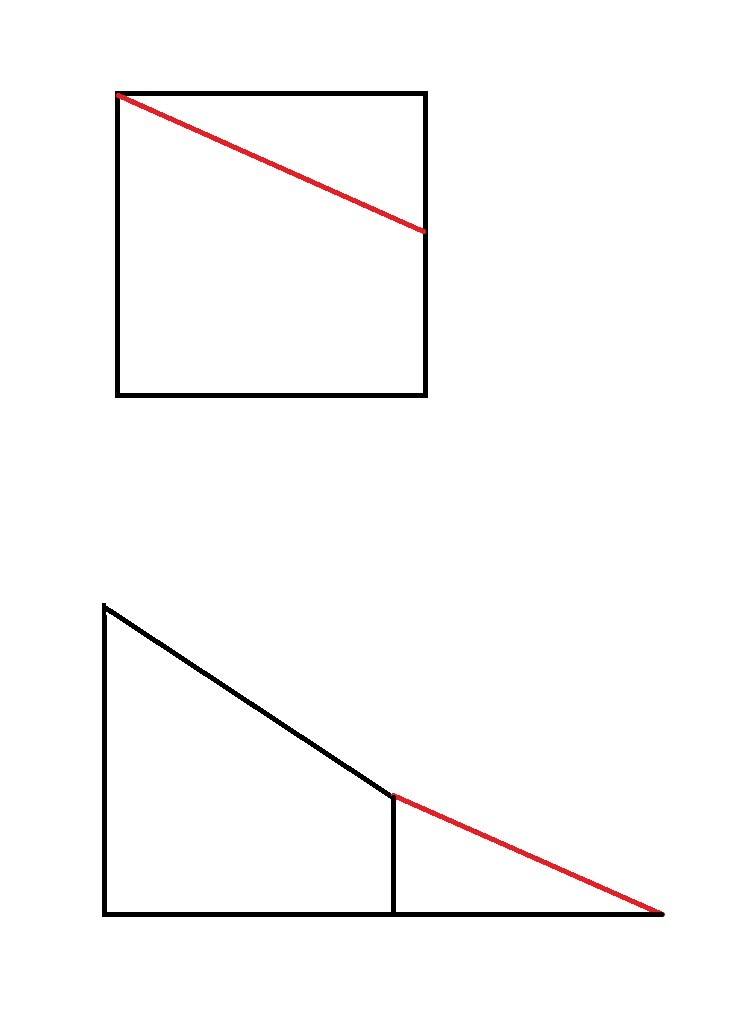
730. Дан прямоугольник, основание которого в два раза больше высоты. 1) Как нужно разрезать данный прямоугольник на две части, чтобы из них можно было составить равнобедренный треугольник? 2) Как нужно разрезать данный прямоугольник на три части, из которых можно было бы составить квадрат?
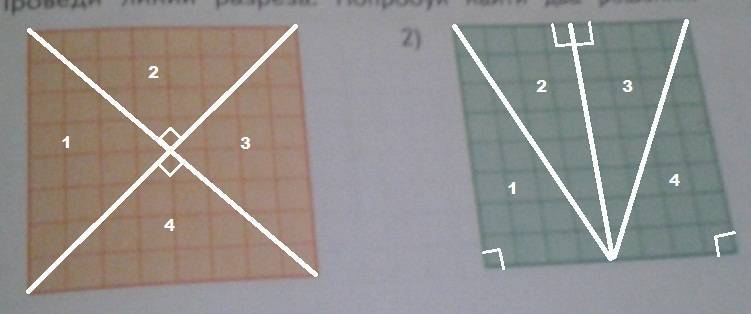
731. Как можно равносторонний треугольник разрезать на: 1) два равных треугольника; 2) три равных треугольника; 3) четыре равных треугольника; 4) шесть равных треугольников; 5) восемь; 6) двенадцать?
732. Даны два равных квадрата. Как разрезать каждый из них на две части так, чтобы из получившихся частей можно было сложить квадрат?
733. Как данный прямоугольник двумя прямолинейными разрезами разбить на два равных пятиугольника и два равных прямоугольных треугольника?
734. Даны два неравных квадрата. Как их следует разрезать на такие части, чтобы из них можно было сложить третий квадрат? Как выражается длина стороны третьего квадрата через длины сторон двух данных?
735. Прямоугольная плитка шоколада состоит из m*n единичных квадратных долек. Сколько разломов нужно сделать (одновременно ломается один кусок), чтобы разломить эту плитку на единичные квадратные дольки?
736. Сколько нужно сделать разрезов плоскостями так, чтобы из куба с ребром в 3 дм получить кубики с ребром в 1 дм?
737. Дан прямоугольный треугольник. Как следует разрезать его на две такие части, чтобы из них (не переворачивая обратной стороной) можно было сложить треугольник, симметричный данному относительно одного из его катетов?
738. Дан треугольник ABC. Как следует разрезать его на части так, чтобы из них (не переворачивая обратной стороной) можно было сложить треугольник, симметричный данному относительно основания АС?
739. Разрежьте квадрат на части, как показано на рисунке 49, перемешайте их и затем сложите: 1) такой же квадрат; 2) прямоугольный равнобедренный треугольник; 3) прямоугольник, отличный от квадрата; 4) параллелограмм, отличный от прямоугольника; 5) трапецию.
Рис.49
740. Окрашенный куб с ребром в 10 см распилили на кубики с ромбом в 1 см. Сколько получится кубиков: 1) с одной окрашенной гранью; 2) с двумя; 3) с тремя; 4) совсем не имеющих окрашенных граней?
741. Как разрезать на две части прямоугольник со сторонами 16 и 9 см так, чтобы из них можно было сложить квадрат? (Разрез может быть в виде ломаной линии.)
742. Скопируйте каждую из фигур рисунка 50 и разрежьте ее на 4 равные части.
Рис.50
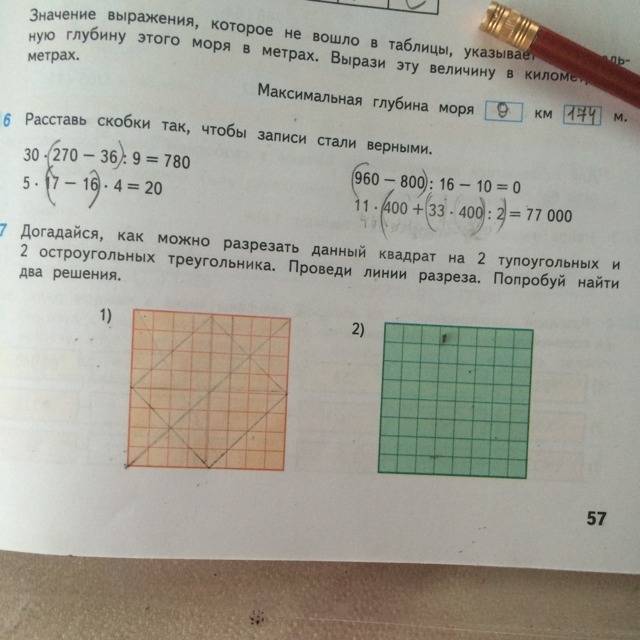
743. 1) Как данный прямоугольный треугольник разрезать на остроугольные треугольники? 2) Как данный произвольный треугольник разрезать на остроугольные треугольники?
744. Внутри выпуклого стоугольника отмечены 10 точек, из которых никакие три не лежат на одной прямой. Многоугольник разрезается на треугольники так, что вершинами их служат все вершины данного стоугольника и все данные десять точек. Сколько получится треугольников?



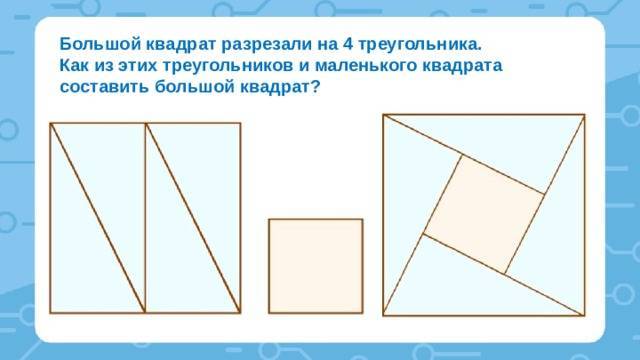
![Разрежьте правильно на части [1984 нагибин ф.ф., канин е.с. - математическая шкатулка]](https://labequip.ru/wp-content/uploads/1/7/0/1704b5b7f0a7679bd63b209e7de534c8.jpeg)




![Разрежьте правильно на части [1984 нагибин ф.ф., канин е.с. - математическая шкатулка]](https://labequip.ru/wp-content/uploads/9/6/4/964f823feaa9f59e231c28b9fa100ba2.jpeg)