Кинетическая энергия пружины

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

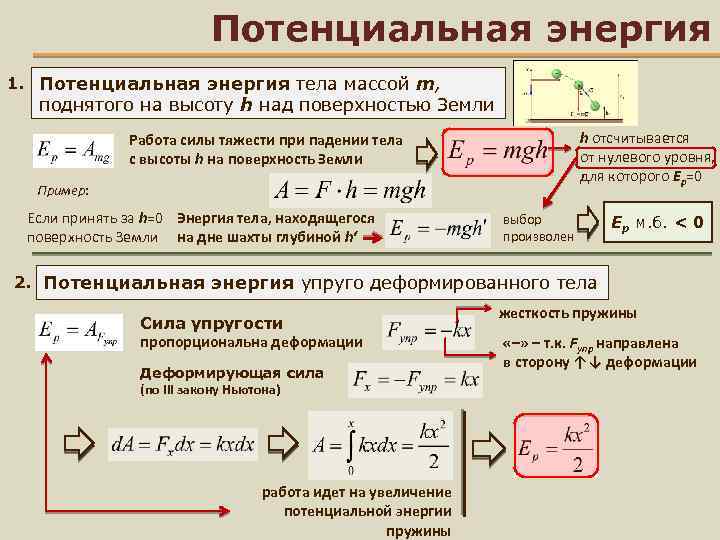
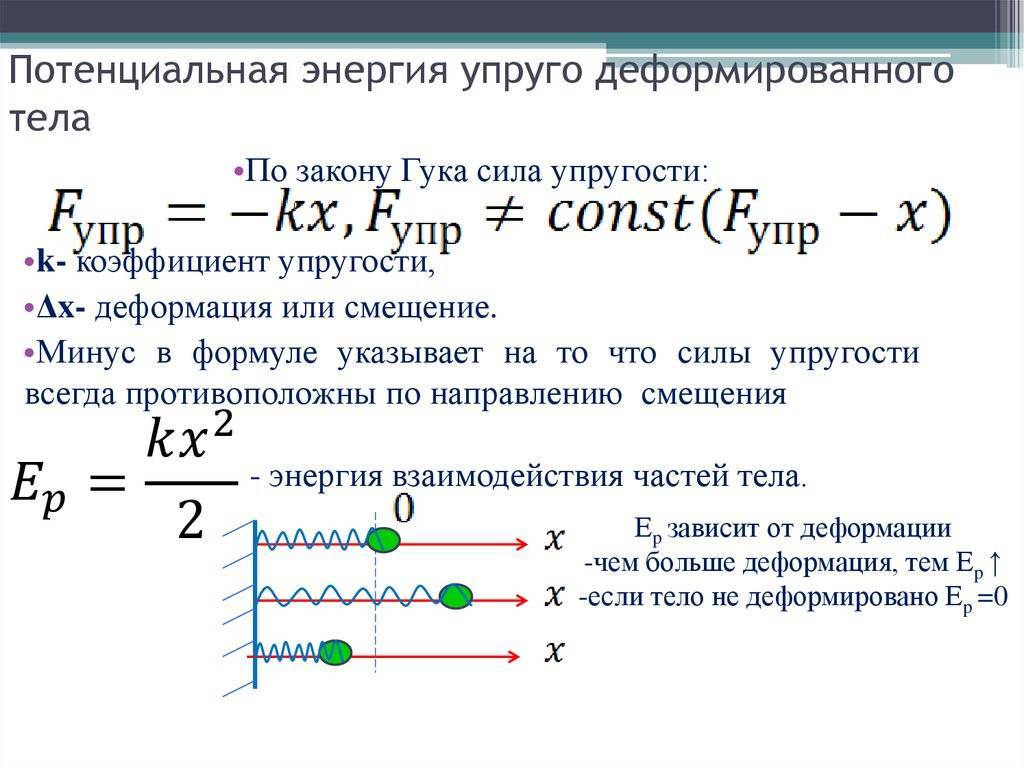
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

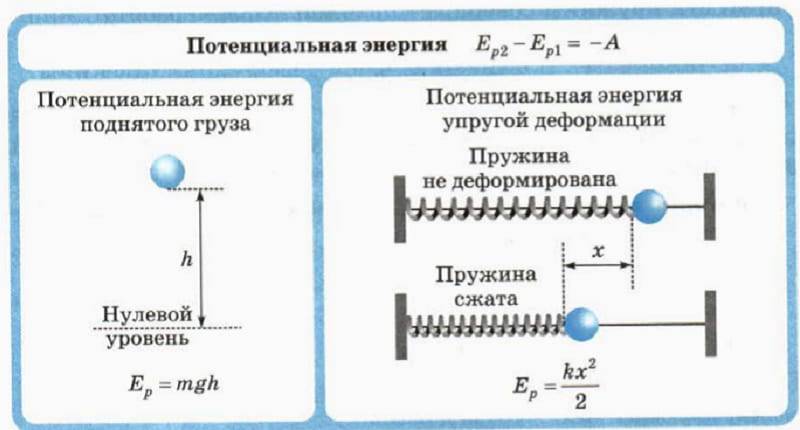
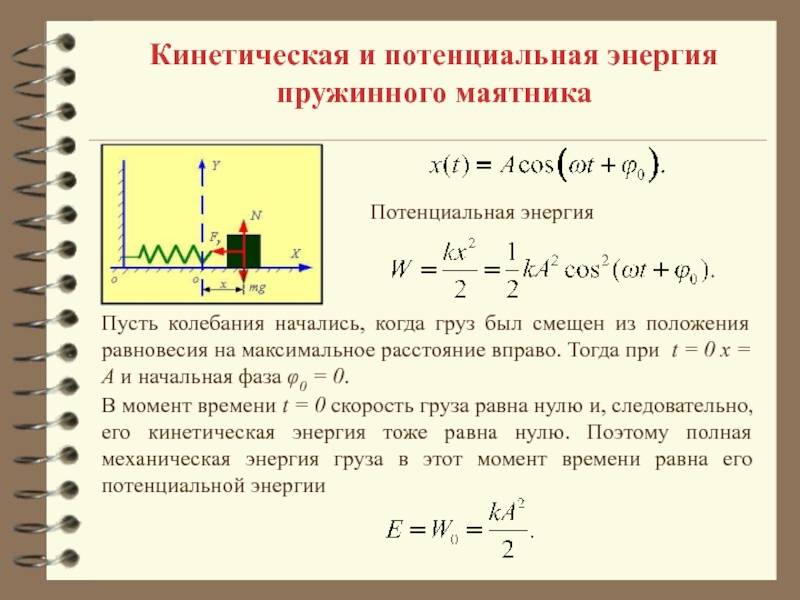
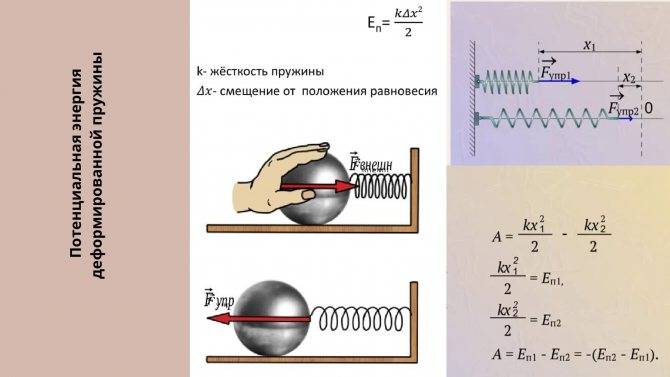
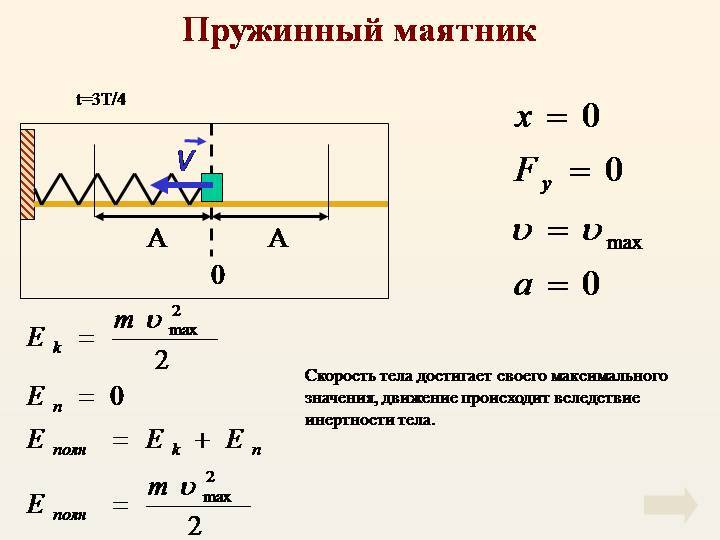
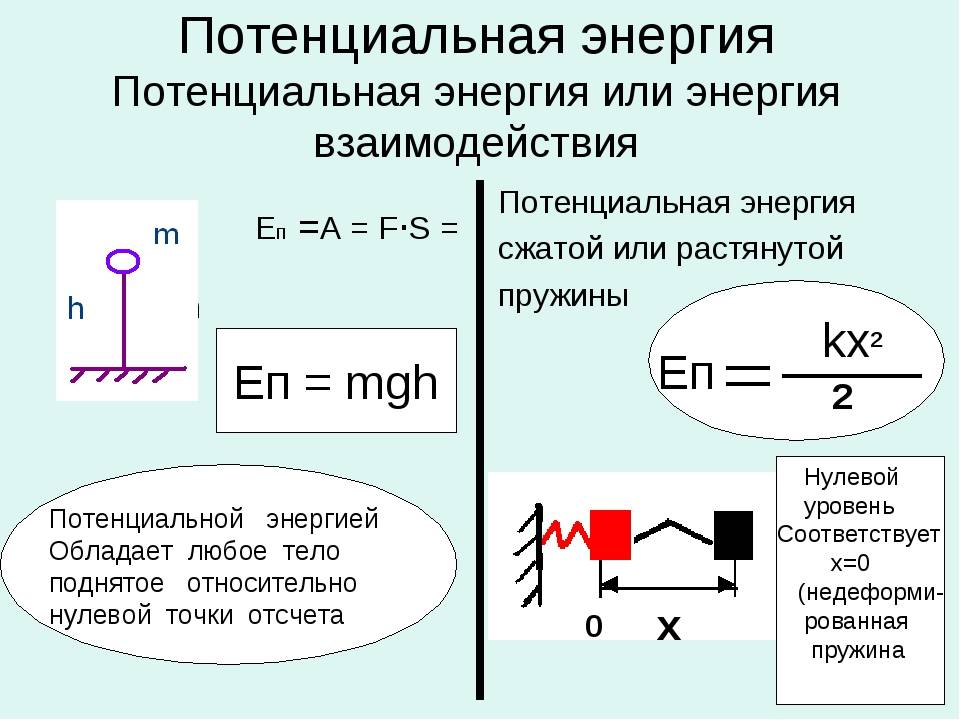
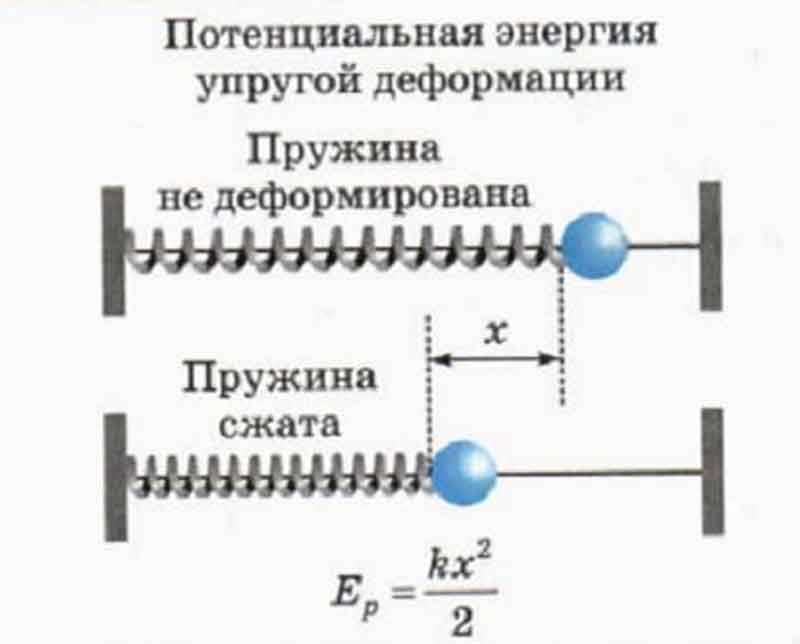
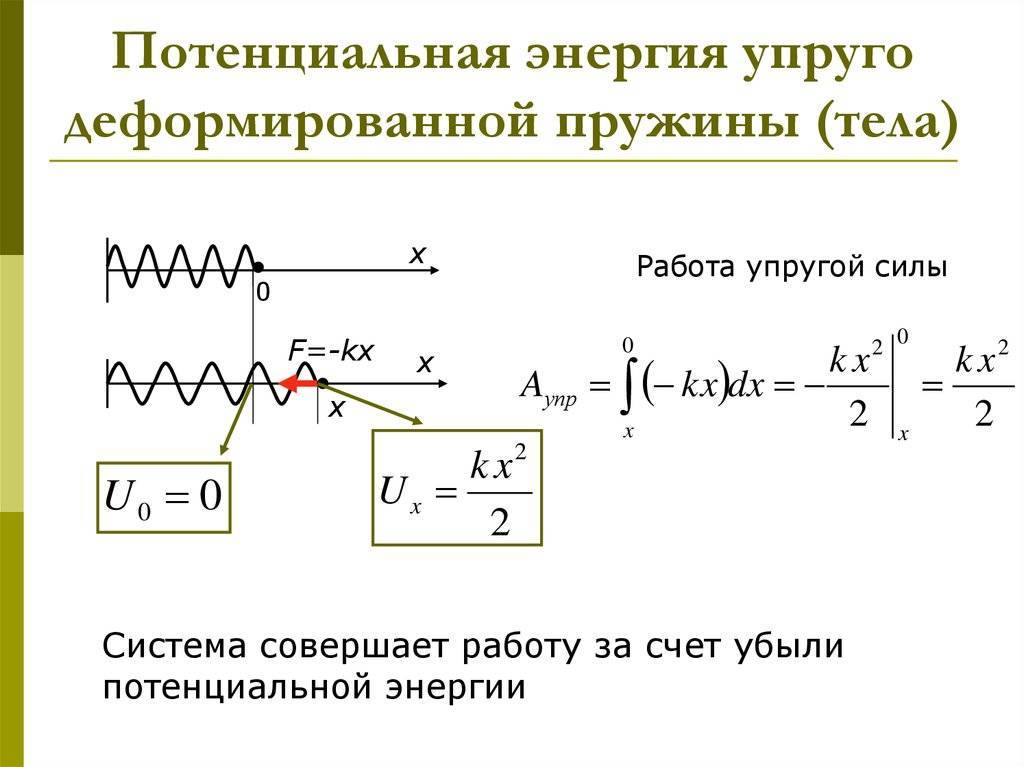
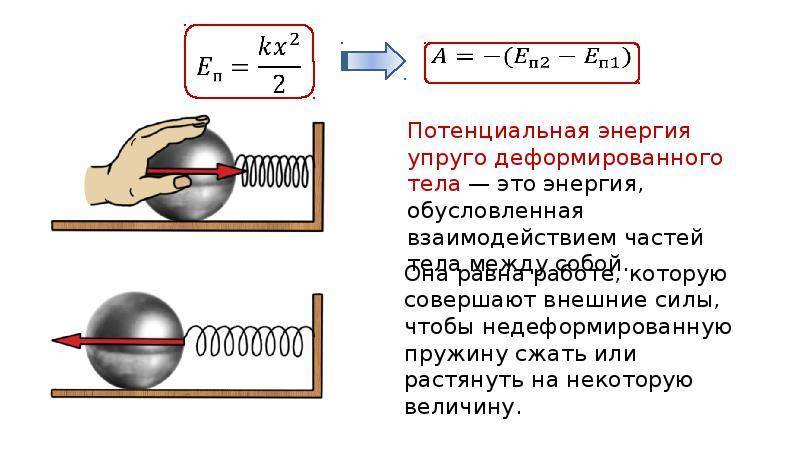
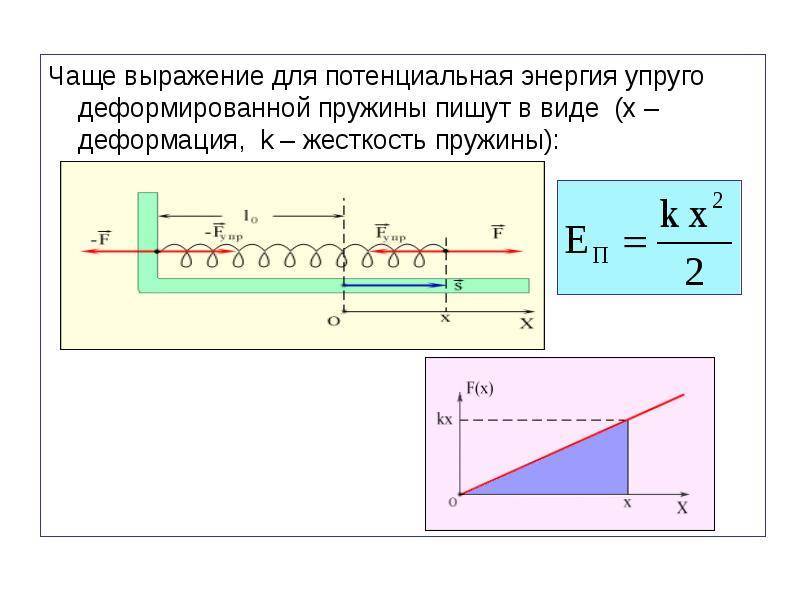
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

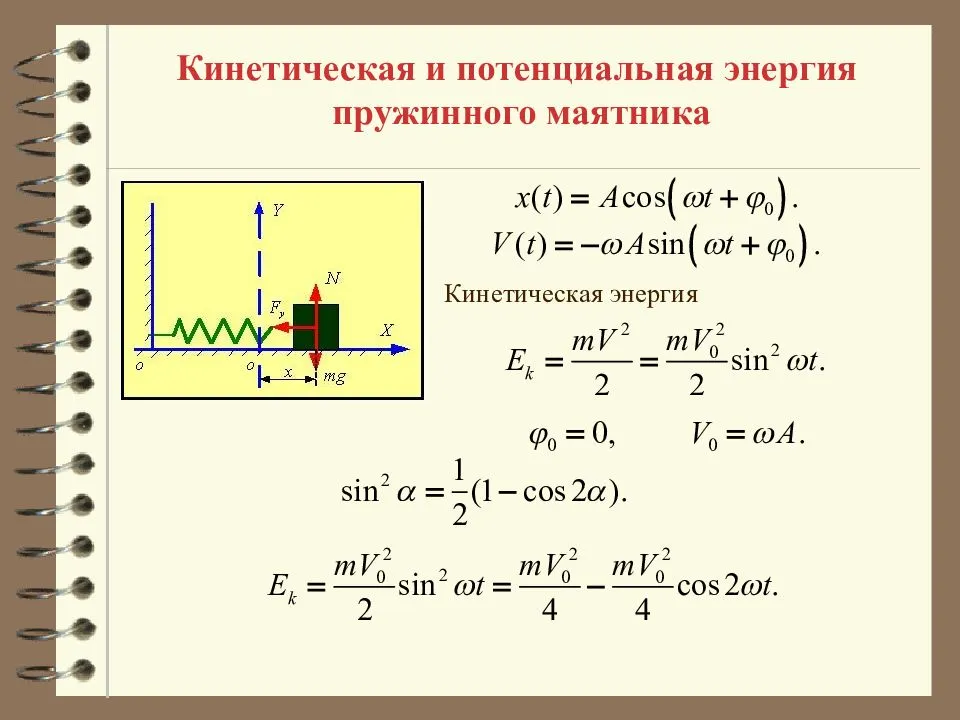
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

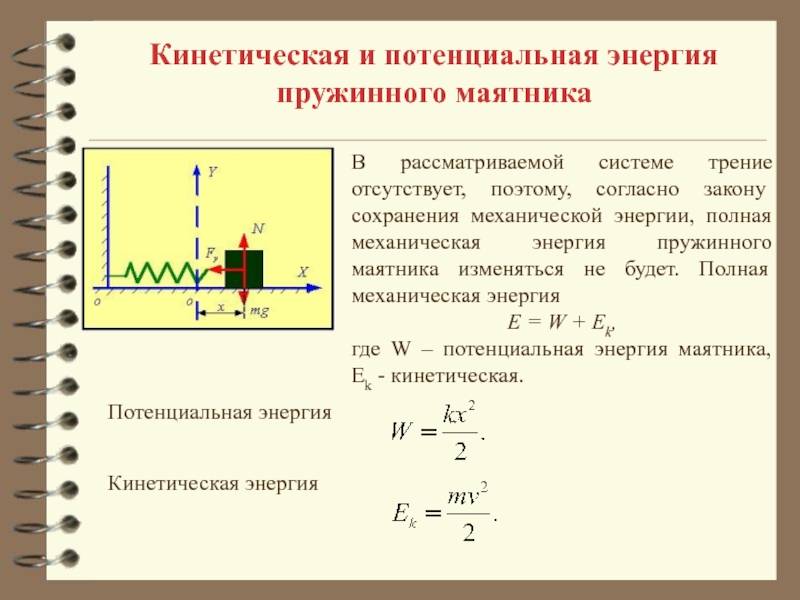
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пру­жин­ный ма­ят­ник, со­сто­я­щий из груза и лёгкой пру­жи­ны, со­вер­ша­ет ко­ле­ба­ния. В мо­мент, когда груз на­хо­дит­ся в край­нем по­ло­же­нии, его не­мно­го под­тал­ки­ва­ют вдоль оси пру­жи­ны в на­прав­ле­нии от по­ло­же­ния

рав­но­ве­сия. Как в ре­зуль­та­те этого из­ме­ня­ют­ся мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка и ча­сто­та его ко­ле­ба­ний?

Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

3) не из­ме­ня­ет­ся

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

Мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка

Ча­сто­та ко­ле­ба­ний ма­ят­ни­ка

Груз под­толк­ну­ли от по­ло­же­ния рав­но­ве­сия, от­ку­да сле­ду­ет, что ам­пли­ту­да ко­ле­ба­ний груза уве­ли­чит­ся. При этом уве­ли­чит­ся также и мак­си­маль­ная по­тен­ци­аль­ная энер­гия пру­жи­ны. По за­ко­ну со­хра­не­ния энер­гии, это при­ве­дет к уве­ли­че­нию мак­си­маль­ной ки­не­ти­че­ской энер­гии груза ма­ят­ни­ка.

Пе­ри­од и ча­сто­та пру­жин­но­го ма­ят­ни­ка за­ви­сят толь­ко от массы груза и жест­ко­сти пру­жи­ны. Таким об­ра­зом, при уве­ли­че­нии ам­пли­ту­ды ко­ле­ба­ний груза, ча­сто­та ко­ле­ба­ний ма­ят­ни­ка не из­ме­нит­ся.

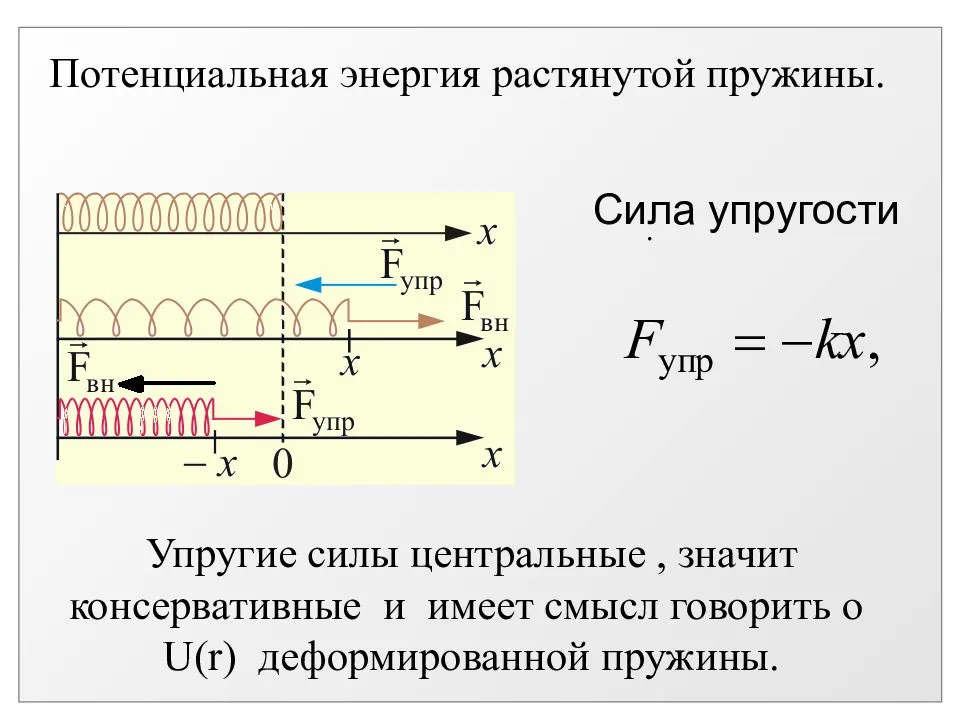
Сила упругости в пружинном маятнике

Следует учитывать тот момент, что до деформирования пружины она находится в положении равновесия. Приложенная сила может приводить к ее растягиванию и сжиманию. Сила упругости в пружинном маятнике рассчитывается в соответствии с тем, как воздействует закон сохранения энергии. Согласно принятым нормам возникающая упругость пропорциональна смещению тела. В этом случае кинетическая энергия рассчитывается по формуле: F=-kx. В данном случае применяется коэффициент жесткости пружины.

Выделяют довольно большое количество особенностей воздействия силы упругости в пружинном маятнике. Среди особенностей отметим:

1. Максимальная сила упругости возникает на момент, когда тело находится на максимальном расстоянии от положения равновесия. При этом в подобном положении отмечается максимальное значение ускорение тела. Не следует забывать о том, что может проводится растягивание и сжатие пружины, оба варианта несколько отличается. При сжатии минимальная длина изделия ограничивается. Как правило, она имеет длину, равную диаметру витка умноженное на количество. Слишком большое усилие может стать причиной смещения витков, а также деформации проволоки. При растяжении есть момент удлинения, после которого происходит деформация. Сильное удлинение приводит к тому, что возникающей силы упругости недостаточно для возврата изделия в первоначальное состояние.
2. При сближении тела к месту равновесия происходит существенное уменьшение длины пружины. За счет этого наблюдается постоянное снижение показателя ускорения. Все это происходит за счет воздействия усилия упругости, которая связано с типом применяемого материала при изготовлении пружины и ее особенностями. Длина уменьшается за счет того, что расстояние между витками снижается. Особенностью можно назвать равномерное распределение витков, лишь только в случае дефектов есть вероятность нарушения подобного правила.
3. На момент достижения точки равновесия сила упругости снижается до нуля. Однако, скорость не снижается, так как тело движется по инерции. Точка равновесия характеризуется тем, что длина изделия в ней сохраняется на протяжении длительного периода при условии отсутствия внешнего деформирующего усилия. Точка равновесия определяется в случае построения схемы.
4. После достижения точки равновесия возникающая упругость начинает снижать скорость перемещения тела. Она действует в противоположном направлении. При этом возникает усилие, которое направлено в обратную сторону.
5. Дойдя крайней точки тело начинает двигаться в противоположную сторону. В зависимости от жесткости установленной пружины подобное действие будет повторятся неоднократно. Протяженность этого цикла зависит от самых различных моментов. Примером можно назвать массу тела, а также максимальное приложенное усилие для возникновения деформации. В некоторых случаях колебательные движения практически незаметны, но они все же возникают.

Приведенная выше информация указывает на то, что колебательные движения совершаются за счет воздействия упругости. Деформация происходит за счет приложенного усилия, которое может варьировать в достаточно большом диапазоне, все зависит от конкретного случая.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела ​\( m_1 \)​ в три раза больше массы другого тела ​\( m_2 \)​. Относительно поверхности Земли потенциальная энергия

1) первого тела в 3 раза больше потенциальной энергии второго тела 2) второго тела в 3 раза больше потенциальной энергии первого тела 3) первого тела в 9 раз больше потенциальной энергии второго тела 4) второго тела в 9 раз больше потенциальной энергии первого тела

2. Сравните потенциальную энергию мяча на полюсе ​\( E_п \)​ Земли и на широте Москвы ​\( E_м \)​, если он находится на одинаковой высоте относительно поверхности Земли.

1) ​\( E_п=E_м \)​ 2) \( E_п>E_м \) 3) \( E_п 4) \( E_п\geq E_м \)

3. Тело брошено вертикально вверх. Его потенциальная энергия

1) одинакова в любые моменты движения тела 2) максимальна в момент начала движения 3) максимальна в верхней точке траектории 4) минимальна в верхней точке траектории

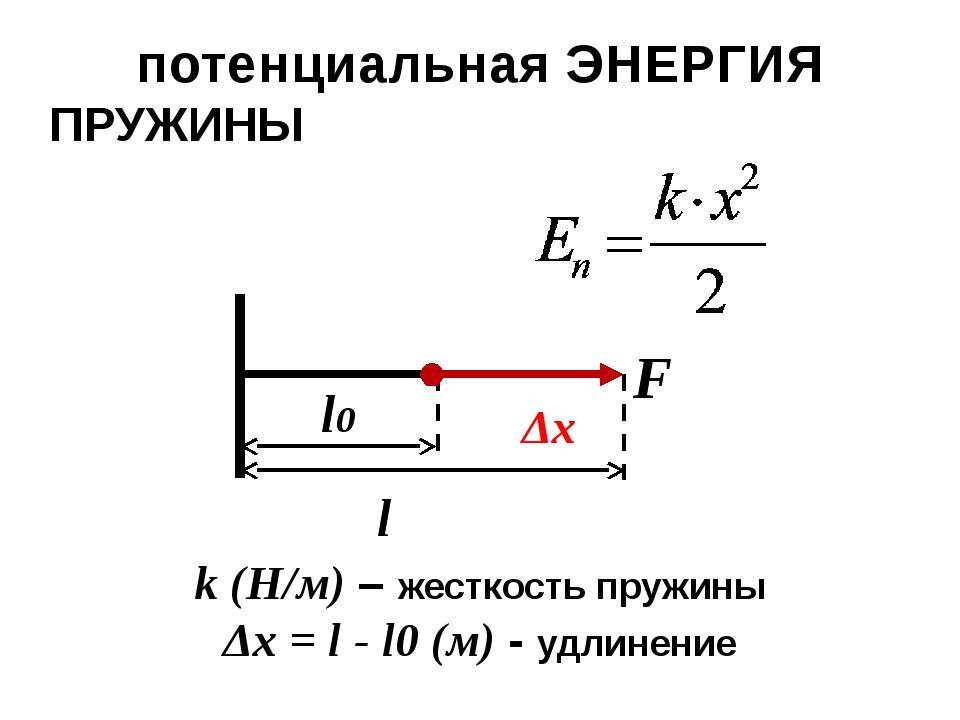
4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?

1) увеличится в 4 раза 2) увеличится в 16 раз 3) уменьшится в 4 раза 4) уменьшится в 16 раз

5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?

1) 0,15 Дж 2) 0,165 Дж 3) 1,5 Дж 4) 1,65 Дж

6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия

1) увеличилась в 16 раз 2) уменьшилась в 16 раз 3) увеличилась в 4 раза 4) уменьшилась в 4 раза

7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела

1) больше в 9 раз 2) меньше в 9 раз 3) больше в 3 раза 4) меньше в 3 раза

8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела

1) минимальна в момент достижения поверхности пола 2) минимальна в момент начала движения 3) одинакова в любые моменты движения тела 4) максимальна в момент начала движения

9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.

1) 0,2 кг 2) 0,288 кг 3) 2,0 кг 4) 2,28 кг

10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.

1) 0,9 м/с 2) 3,0 м/с 3) 4,5 м/с 4) 9,0 м/с

11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА A. Потенциальная энергия взаимодействия тела с Землёй Б. Кинетическая энергия B. Потенциальная энергия упругой деформации

ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ 1) ​\( E=mv^2/2 \)​ 2) \( E=kx^2/2 \)​ 3) \( E=mgh \)​

12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА A. Потенциальная энергия Б. Кинетическая энергия B. Полная механическая энергия

ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ 1) Уменьшается 2) Увеличивается 3) Не изменяется

Часть 2

13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.

Механическая работа. Мощность

\(A = F \cdot \Delta r \cdot \cos \alpha\) , где А

– работа (Дж);F – сила (Н); Δr – перемещение тела (м);α – угол между вектором силы и вектором перемещения (рис. 1).

Данную формулу можно применять, если сила постоянна.

• а. А

  > 0 , 0° ≤α < 90° угол острый

• б. А

  = 0 ,α = 90° угол прямой

• в. А

  < 0 , 90° <α ≤ 180° угол тупой

Рис. 1 Aтр = -Fтр·Δr ,

где Aтр – работа силы трения (Дж); Fтр – сила трения (Н); Δr

– перемещение тела (м).

Работа силы трения отрицательная, т.к. сила трения и относительное перемещение тела направлены в противоположные стороны.

\(~P = \frac{A}{\Delta t}\) , где Р

– мощность прибора (Вт);А – механическая работа, совершенная данным прибором (Дж); Δt – время, за которое совершена работа (с). \(~\eta = \frac{A_p}{A_z}\) или \(~\eta = \frac{A_p}{A_z} \cdot 100%\) , где η

– коэффициент полезного действия (КПД) (%);А p – полезная работа (Дж);А z – затраченная работа (Дж).

• Полезная работа – это работа, которую совершает механизм над телом,
• затраченная работа – это работа двигателя или энергия (тепловая, электроэнергия и т.п.), которую механизм израсходует (получает).

Графический способ определения механической работы

Пусть задан график зависимости проекции силы Fx

от координатых . Тогда работа при перемещении тела из точки с координатойx 1 в точку с координатойx 2 численно равна по величине площади фигуры, ограниченной графикомFx (х ), осью0Х и перпендикулярами кx 1 иx 2 (рис. 2).

Рис. 2

• При перемещении тела из точки с координатой x 2 в точку с координатойx 1 площадь фигуры и, следовательно, работу будем считать отрицательной.
• Если разные участки тела поднимают на разные высоты, то изменение потенциальной энергии можно рассчитать для центра тяжести тела.
• Центр тяжести стержня находится в середине стержня; прямоугольника – на пересечении диагоналей; шара, обруча – в центре сферы, окружности.

Уравнение движения вращающегося тела

Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек

При этом отметим нижеприведенные особенности:

1. Прямая, которая соединяет две точки, выступает в качестве оси вращения.
2. Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
3. Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.

Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt

В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Контрольные вопросы

Что называется деформацией? Какие деформации называются упругими? Приведите примеры упругих деформаций.

Какова физическая сущность упругих сил?

Сформулируйте закон Гука? Когда он справедлив?

Дайте объяснение качественной диаграмме напряжений. Что такое предел пропорциональности, упругости и прочности?

Что такое упругий гистерезис и упругое последействие?

Каков физический смысл модуля Юнга и модуля сдвига?

Что такое упругое последействие?

Выведите выражения для деформаций при всестороннем растяжении.

Что называется коэффициентом Пуассона?

Определите энергию деформированного тела.

Что называется плотностью упругой энергии? Получите формулы этой энергии при растяжении и сдвиге.

А. mv²/2 Б.mv В.mgh Г. kx²/2 2. Каково наименование единицы кинетической энергии, выраженное через основные единицы Международной системы? А.1кг·м Б.1 кг·м/с В.1кг·м²/с Г.1кг·м²/с² 3. Чему равна кинетическая энергия тела массой 3 кг, движущегося со скоростью 4 м/с?

Читать также: Почему стиральная машинка сильно вибрирует при отжиме

А. 6 Дж. Б. 12 Дж. В.24Дж. Г.48Дж.

4. Как изменится потенциальная энергия упруго деформированного тела при увеличении его деформации в три раза?

À. Не изменится. Б. Увеличится в 3 раза. . Увеличится в 9 раз. Г. Увеличится в 27 раз.

Два автомобиля с одинаковыми массами m движутся со скоростями v и 3v относительно Земли в одном направлении. Чему равна кинетическая энергия второго автомобиля в системе отсчета, связанной с первым автомобилем?

А.mv² Б.2mv² В.3mv² Г.4mv² 6.Каково наименование единицы работы, выраженное через основные единицы Международной системы? А.1кг Б.1кг·м/с В.1кг·м/с² Г.1кг·м²/с² 7.По какой формуле следует рассчитывать работу си­лы F, если между направлением силы и перемещения S угол a ? А.(F/S)·cosα Б.F·S·sinα В.F·S·cosα Г.(F·S)·sinα

9. Тело массой 1 кг силой 30 Н поднимается на высо­ту 5 м. Чему равна работа этой силы?

А .0 Дж. Б. 50 Дж. В. 100 Дж. Г. 150 Дж.

Кинетическая энергия тела в момент бросания равна 200 Дж. Определите, до какой высоты от поверхности земли может подняться тело, если его масса равна 500 г.

Башенный кран поднимает бетонную плиту массой 2 т на высоту 15 м. Чему равна работа силы тяжести, действующей на плиту?

Формула определения жесткости

Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или

равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).

Другой вариант записи формулы: коэффициент Юнга

Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.

Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.

К примеру, модуль Юнга для ста

ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).

Смысл понятия коэффициент жесткости

Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.

Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).

Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:

• Материала, используемого при ее изготовлении.
• Формы и конструктивных особенностей.
• Геометрических размеров.

По этому показателю можно сд

елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.

Особенности расчета пружин

Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.

Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.

Например:

• Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
• При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.

Что такое кинетическая энергия

Кинетическая энергия – это энергия, создаваемая движущимся телом. На греческом языке кинетика означает «движение», в то время как энергия означает «работа». Другими словами, кинетическая энергия – это работа, которую тело выполняет, когда оно движется.

Мы можем воспользоваться кинетической энергией многих природных явлений. Например, движение воды в реке превращается в электричество благодаря электростанциям. Энергия ветра – это кинетическая энергия воздуха. Когда мы прибиваем гвоздь молотком, мы используем кинетическую энергию молотка при его перемещении.

Кинетическая энергия в физике измеряется в джоулях , сокращенно буквой J.

Формула кинетической энергии

Для расчета кинетической энергии тел используется уравнение:

Это означает, что кинетическая энергия Ec равна массе тела m, умноженной на квадрат скорости v, делённые на 2.

Мы можем сделать вывод, что чем больше масса, тем больше энергия, и что энергия пропорциональна скорости, умноженной на себя.

Кинетическая энергия не является вектором. Это означает, что если вы бросаете шар со скоростью 5 м / с, шар будет иметь одинаковую кинетическую энергию, независимо от того, бросаете ли вы его влево или вправо или вверх.

Кинетическая энергия зависит от массы и скорости

Гоночные машины спроектированы с наименьшей массой для улучшения характеристик.

Кинетическая энергия зависит от массы и скорости тела. Это означает, что чем больше или быстрее объект, тем больше энергии он производит.

Примером вышесказанного может быть следующее: грузовик больше, чем автомобиль; Если оба едут с одинаковой скоростью и врезаются в стену, урон, нанесенный грузовиком, будет больше. В этом случае грузовик обладает большей кинетической энергией.

А теперь представьте: две одинаковые машины едут, одна со скоростью 50 км / ч, а другая со скоростью 100 км / ч. Чем выше скорость, тем серьезнее авария.

Таким образом, кинетическая энергия зависит от квадрата скорости. Это означает, что когда скорость объекта удваивается, его кинетическая энергия увеличивается в четыре раза.

Автомобиль, движущийся со скоростью 60 км / ч, имеет в четыре раза больше кинетической энергии, чем автомобиль, движущийся со скоростью 30 км / ч, и, следовательно, в четыре раза больший потенциал разрушения в случае аварии.

Как рассчитать кинетическую энергию тела?

В аэропорту хотят рассчитать кинетическую энергию 30-килограммовой упаковки в системе, которая движется со скоростью 0,500 м / с. Как мы это делаем?

• Мы знаем массу и скорость упаковки, поэтому используем формулу:
• Подставляя значения, имеем:

Рассуждение

Единицей кинетической энергии является джоуль, которая является той же для единицы работы

Обратите внимание, что, несмотря на то, что он тяжелый, его кинетическая энергия не так велика из-за его низкой скорости

Ключевые моменты для запоминания

• Тело имеет кинетическую энергию, только если оно находится в движении.
• Кинетическая энергия зависит от массы и скорости тела.

Задача 1 на нахождение кинетической энергии

Слон в 6000 кг бежит со скоростью 10 м / с. Какова его кинетическая энергия? Какова скорость пушечного ядра весом 1 кг, если у него была та же самая кинетическая энергия слона?

Ответ

Используя уравнение кинетической энергии, энергия слона равна:

Рассчитав кинетическую энергию, мы можем получить скорость пули, очистив v:

Это означает, что скорость пули равна 775 м / с. Сравните это со скоростью слона: вот это разница!

Задача 2

Мужчина врезался в столб на своей машине. Когда он пошел, чтобы сообщить о катастрофе, он сказал, что ехал с допустимой скоростью во время аварии.

Но следователь помнил физику 7 и 8 класса и установил, что скорость транспортного средства была в два раза выше, чем утверждал водитель.

Какова взаимосвязь между кинетической энергией и скоростью, сообщаемой человеком, и кинетической энергией со скоростью, рассчитанной следователем?

Мы будем рассматривать Ec1 как кинетическую энергию транспортного средства на скорости v1, сообщаемой человеком, и Ec2 как кинетическую энергию со значением скорости v2, рассчитанным исследователем. Соотношение между кинетическими энергиями рассчитывается путем деления энергий следующим образом:

1. Следователь сказал, что скорость во время аварии была вдвое выше, чем сообщал человек, то есть:
2. Подставим значение скорости в уравнение:

Исключая похожие термины, мы имеем:

Это означает, что кинетическая энергия в соответствии со скоростью, сообщаемой человеком, составляет четверть кинетической энергии по расчетам следователя. Проще говоря, ущерб, нанесенный автомобилем, был в четыре раза больше, чем сообщал мужчина.