Конусность и уклон: построение, расчет, обозначение

Как осуществлять контроль изготовления конических поверхностей

Внешние конуса измеряются с помощью универсального угломера либо специального шаблона. Калибр-втулки служат для проверки точных параметров конуса. Кроме угла конуса, они показывают и его сечения. Карандашом наносят на обработанную поверхность несколько меток. Калибр-втулку помещают сверху на контрольный конус.

Рис. 8. Калибр-втулка для проверки наружных конусов (а) и пример ее применения (б):

A, B – метки

Поворачивая инструмент в разные стороны и легко нажимая на него, добиваются, что метки на качественно обработанном конусе стираются полностью. Конец конусной детали должен быть расположен между отметками А и В.

Контроль конических отверстий осуществляют калибром-пробкой. Качество отверстия показывает плотность прилегания калибра к обработанной поверхности. Нанесением тонкого слоя красящего вещества на пробку калибра, можно определить: если краска исчезнет возле большого сечения – угол конуса занижен, если возле малого – увеличен.

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.

К особенностям построения угла и конусности можно отнести следующие моменты:

1. Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
2. При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
3. Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.

В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.

Часто для отображения уклона в начертательной геометрии создаются дополнительные линии, а также обозначается угол уклона.

В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

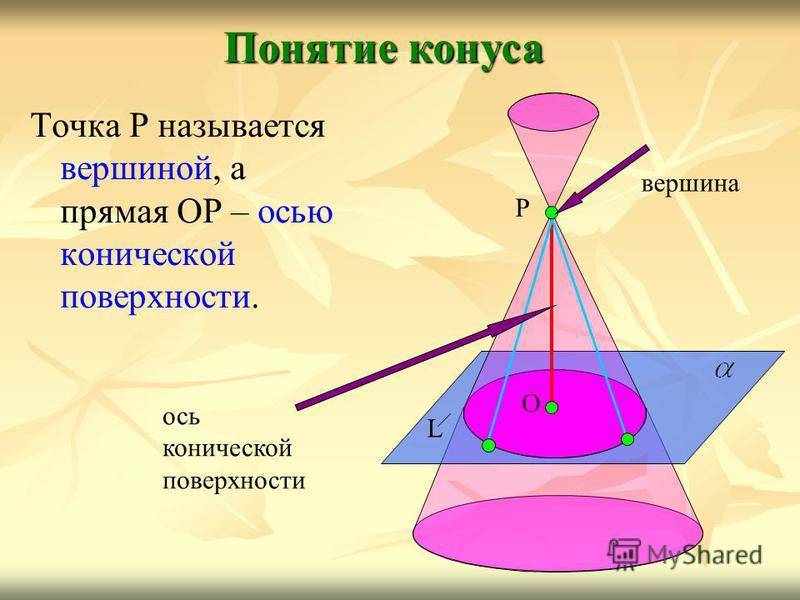
Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

4

Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

5

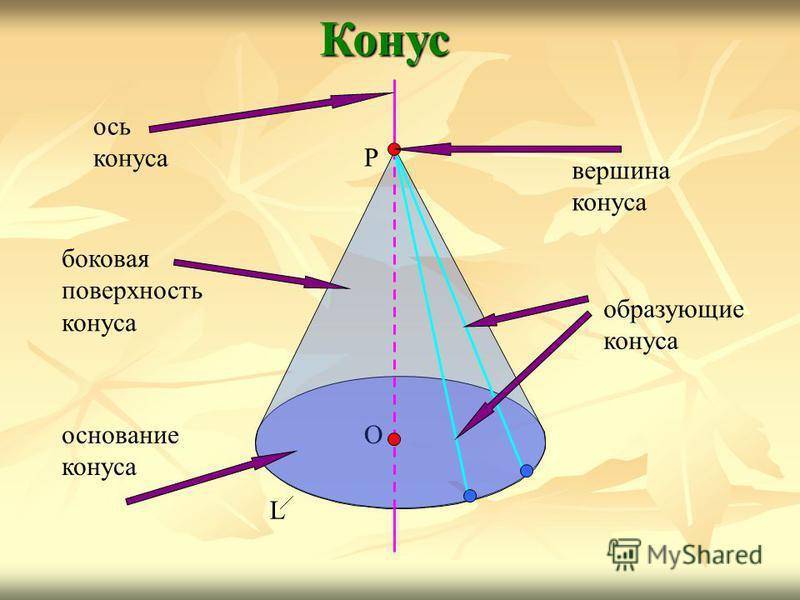
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

6

Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

7

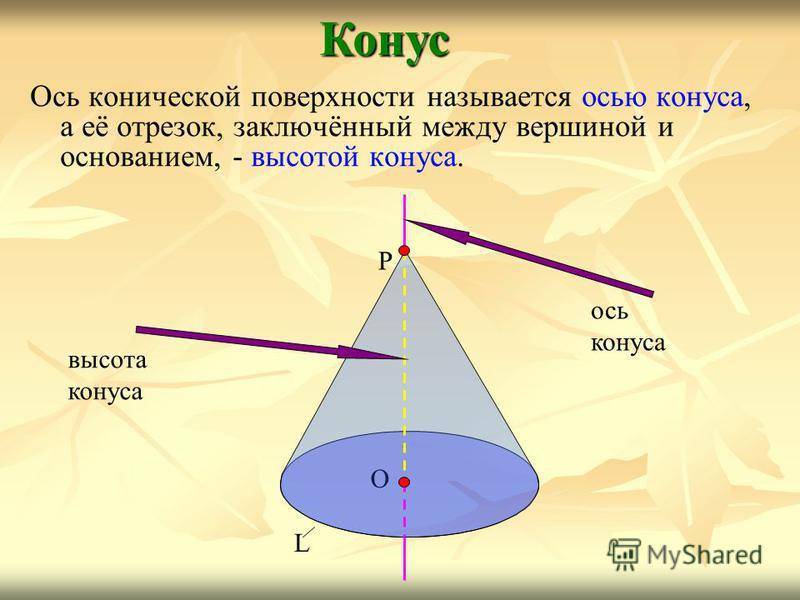
Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

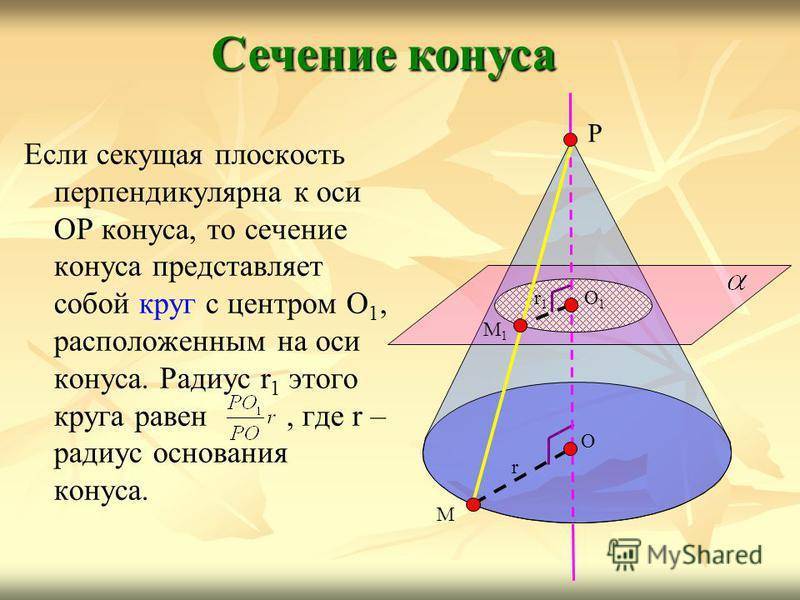
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

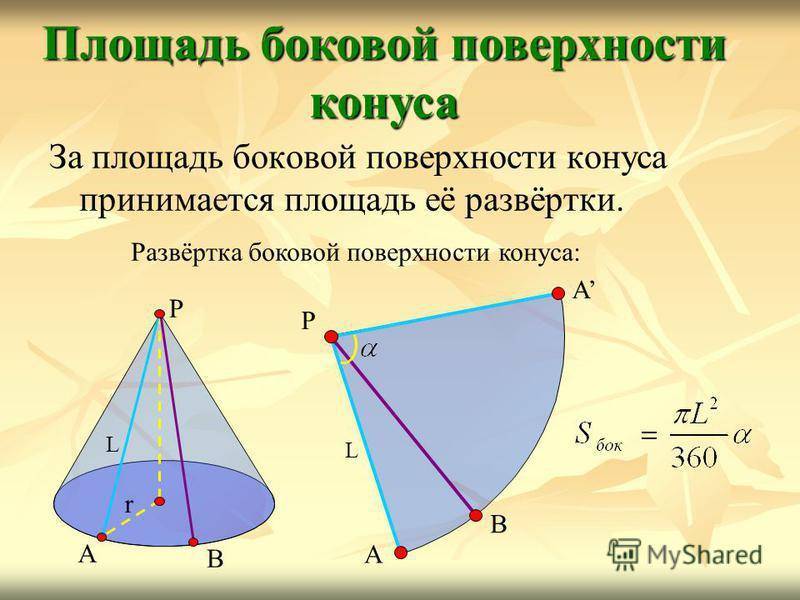
13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

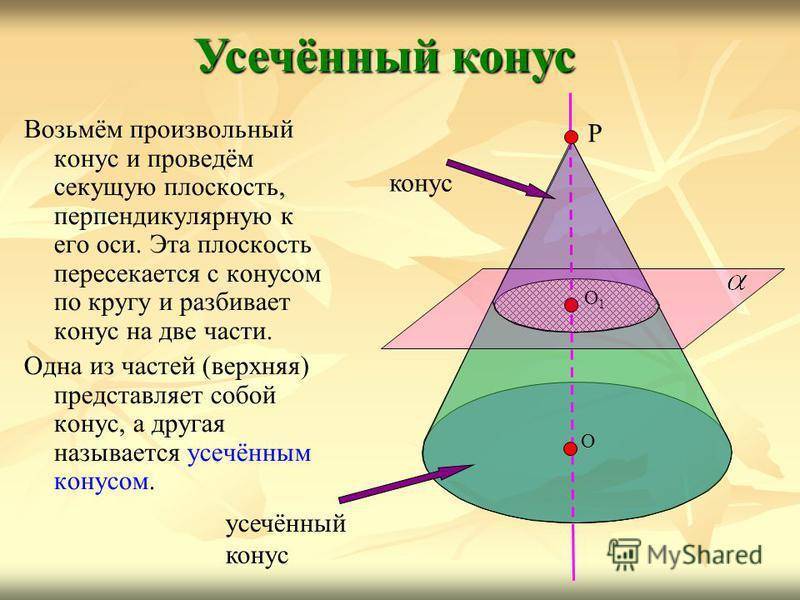
16

Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

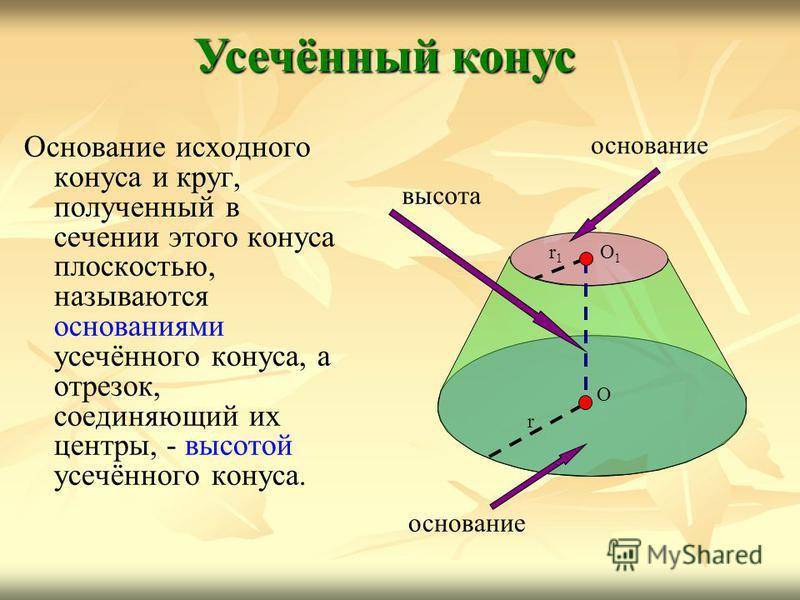
17

Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

18

Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

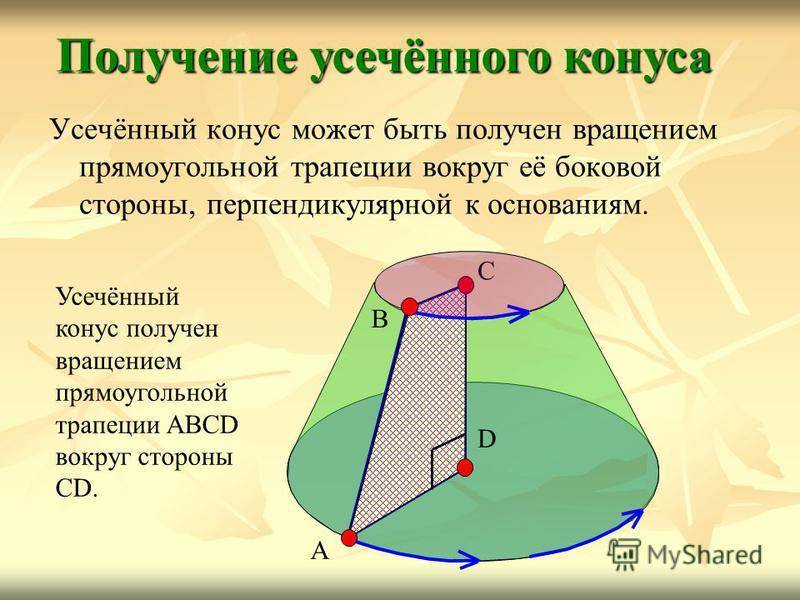
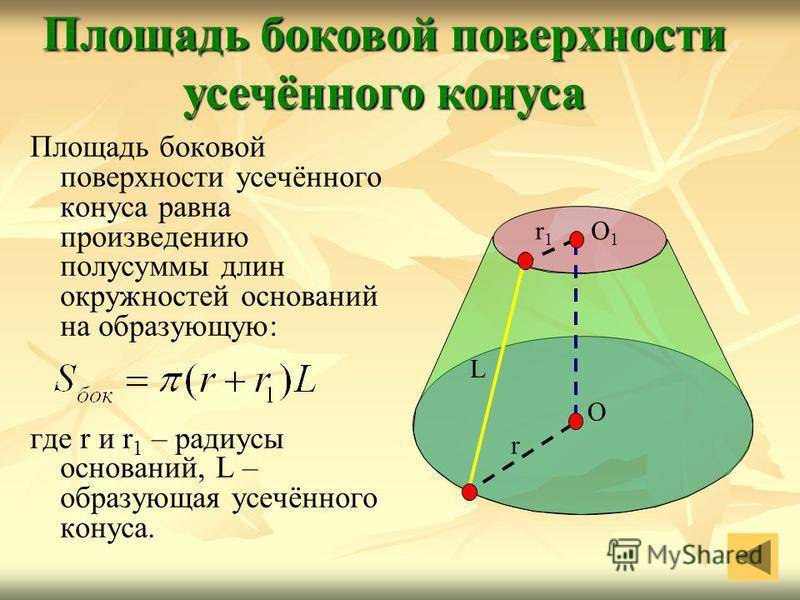
19

Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

Параметры конической трубной резьбы

Данный вид соединений обозначается исключительно в дюймах. Указываются значения в целых и дробных частях. Профиль конической трубной резьба отличается от стандартного дюймового аналога. Угол при вершине составляет 55° в первом случае и 60° во втором. В отдельных случаях допускается соединения обоих видов. Условия определены в ГОСТ 6211–81. В § 4.7 сказано, что в этом случае можно использовать наружную трубную коническую резьбу совместно с цилиндрической внутренней. Номинальные значения должны совпадать. Например, диаметр 1½ должен быть одинаковым у обеих деталей. Внутренняя трубная дюймовая коническая резьба не соединяется наружным цилиндрическим элементом.

Гост 25557-2006 конусы инструментальные. основные размеры

Этот параметр одинаков для всех видов конической трубной резьбы, а вот шаг существенно отличается. Исторически принято измерять его в количестве ниток на дюйм. Но в процессе эволюции производства некоторые значения не соответствуют указанным данным. Поэтому вся дюймовая резьба сегодня имеет расшифровку в привычных европейских стандартах. Метрическая система измерения гораздо удобнее в работе.

Ниже указаны соответствия дюймовых номиналов аналогам в мм:

• ⅛ — 28 (число ниток на дюйм), 0,907 мм;
• ¼ — 19, 1,337 мм;
• ⅜ — 19, 1,337 мм;
• ½ — 14, 18,14 мм
• ¾ — 14, 18,14 мм
• 1 — 11, 23,09 мм
• 1¼ — 11, 23,09 мм
• 1½ — 11, 23,09 мм
• 2 — 11, 23,09 мм

У конической трубной резьбы различают три диаметра: наружный, внутренний и средний. Чертеж соединения выполнен в виде трапеции. Ее основание — наружная резьба, вершина внутренняя. Среднее значение вычисляется математически. Оно примерно соответствует размерам обычной цилиндрической дюймовой резьбы

Это важно знать при совмещении различных типов соединения. То есть, когда конусная деталь вкручивается в обычную дюймовую резьбу, то вначале вращения соединение получается прослабленное. К середине длины оно уплотняется, дальше движение производится с увеличивающимся натягом

Преимущества конуса часто используется в стандартных соединениях при прослабленной внутренней резьбе. Если деталь изношена и внутреннее отверстие становится больше нормы, то можно заменить цилиндрический элемент. Угол конуса компенсирует прослабление по диаметру

К середине длины оно уплотняется, дальше движение производится с увеличивающимся натягом. Преимущества конуса часто используется в стандартных соединениях при прослабленной внутренней резьбе. Если деталь изношена и внутреннее отверстие становится больше нормы, то можно заменить цилиндрический элемент. Угол конуса компенсирует прослабление по диаметру.

Следует знать, что при подготовке деталей к обработке необходимо учитывать припуски. Делая конус на входящей детали ориентируются на наружное значение диаметра по таблице. Затем проверяют длину заготовки и лишь потом делают нужный уклон. На токарном станке выставляют угол на верхней каретке суппорта. Второй вариант — использование фасонного резца. В обоих случаях придется делать ручную настройку, и точно выставить режущий инструмент сложно, поэтому обязательно проверяют угол специальным калибром.

Угол вершины профиля 55° выбран не случайно. Это гарантирует лучшую герметизацию соединения. При закручивании происходит притирка деталей с легким заминанием профиля. Однако применять силу при сборке не рекомендуется. Конусность деталей приводит к тому, что вектор нагрузки направлен наружу. Деталь может просто разорвать при избыточных усилиях. Особенно, если толщина элемента с внутренней резьбой небольшая. Не рекомендуется применять технологию на тонкостенных латунных и алюминиевых деталях. Об этом нужно помнить, когда решено сочетать трубную коническую и трубную цилиндрическую резьбу, которая не рассчитывалась при производстве на такой вид нагрузки.

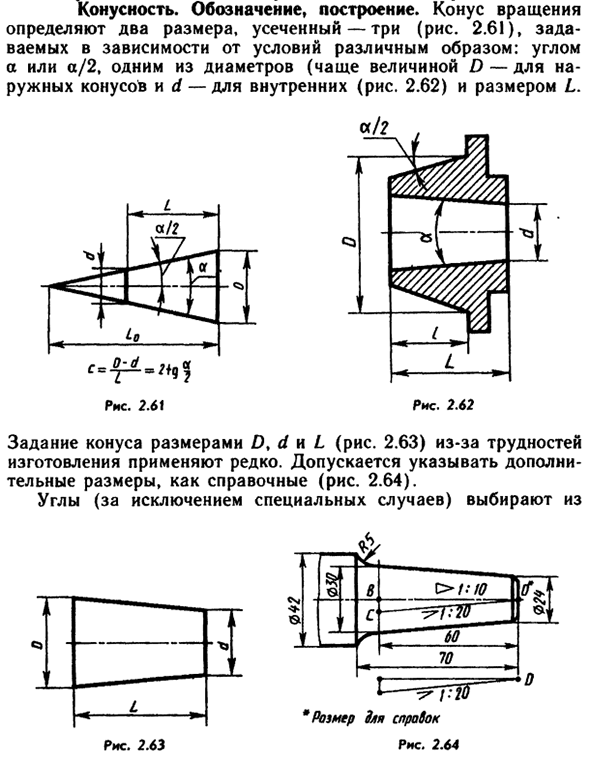
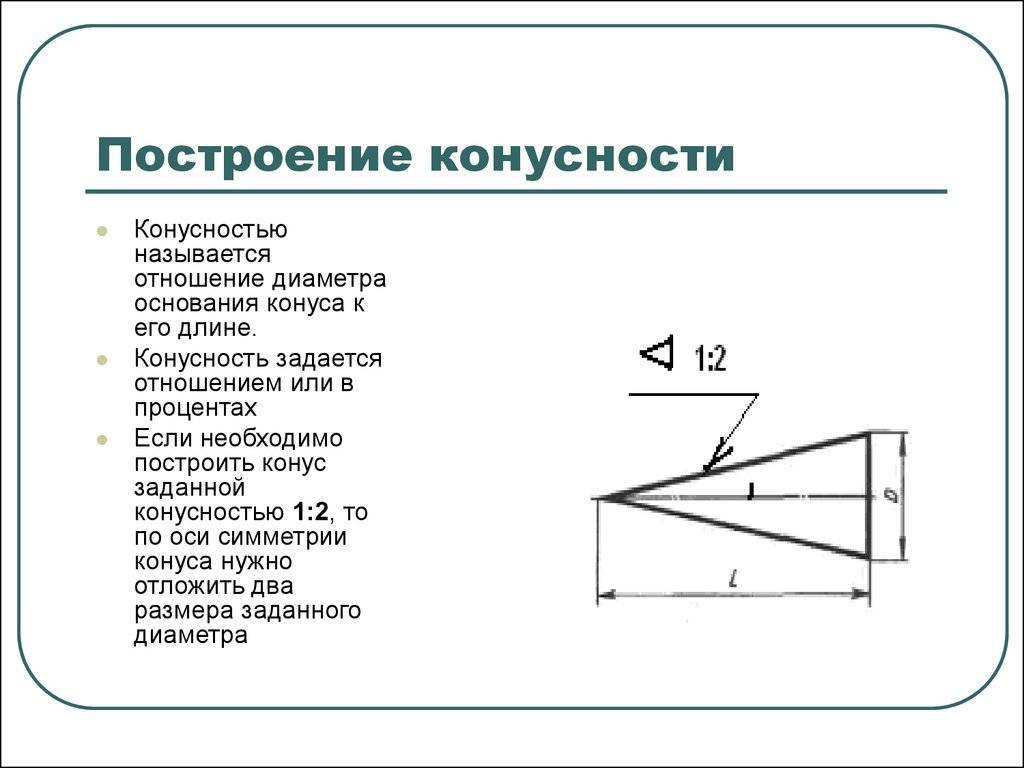
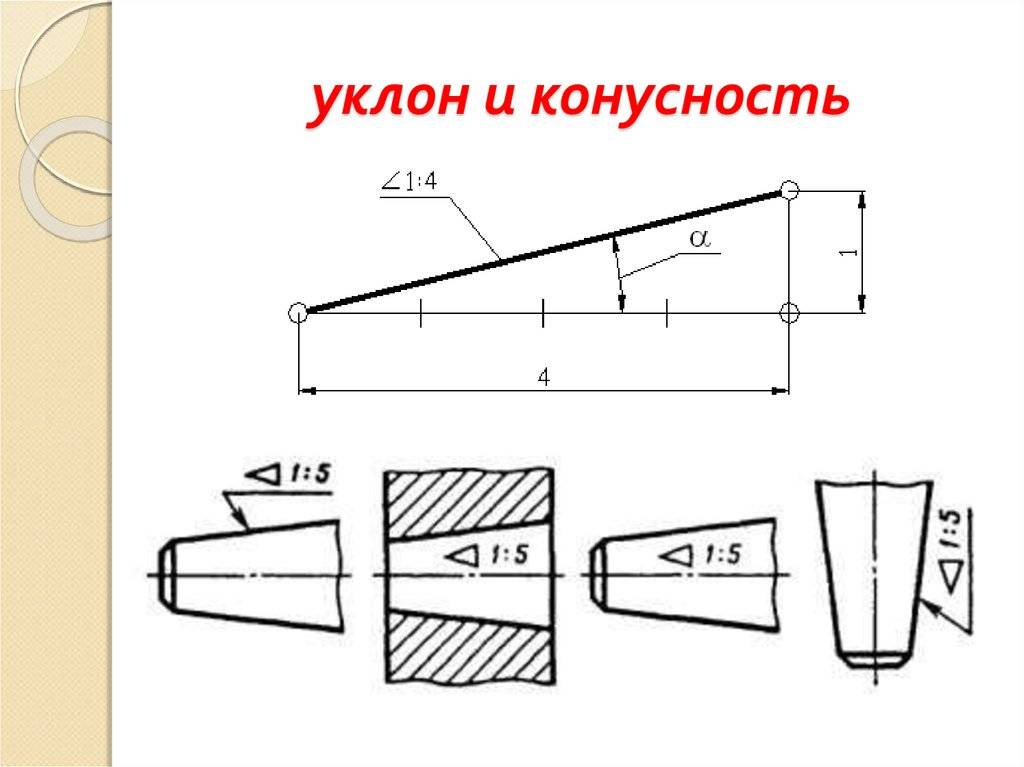
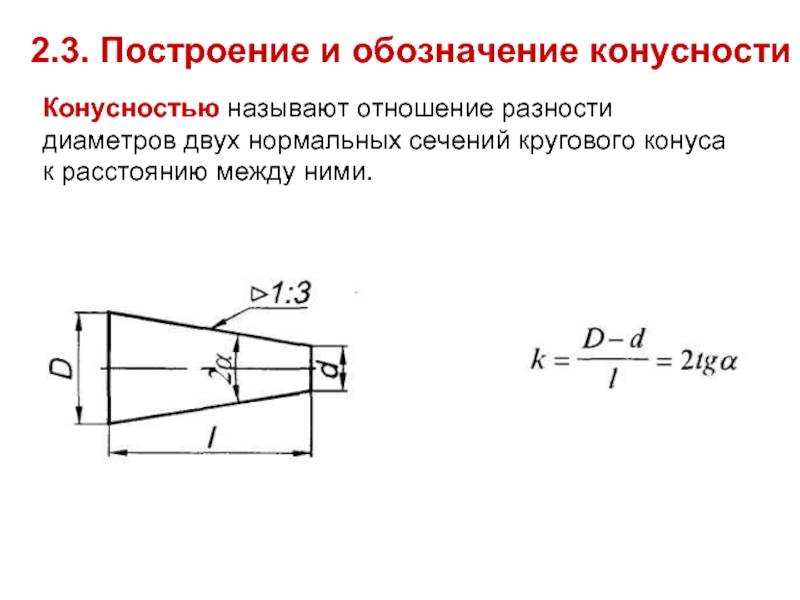
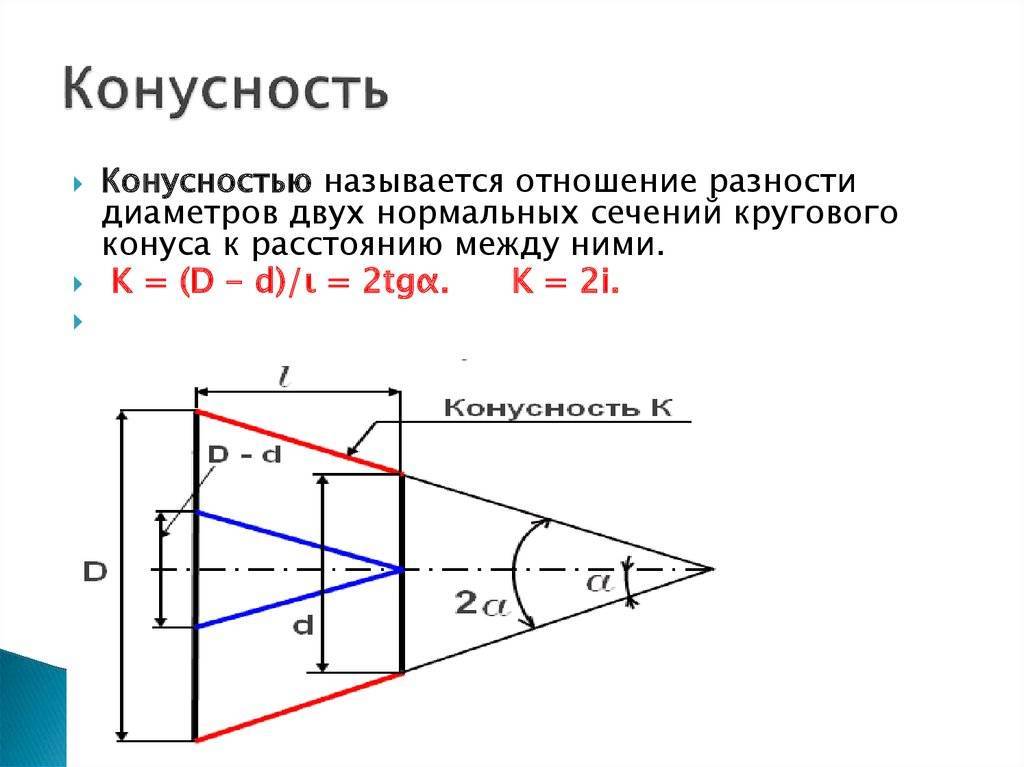
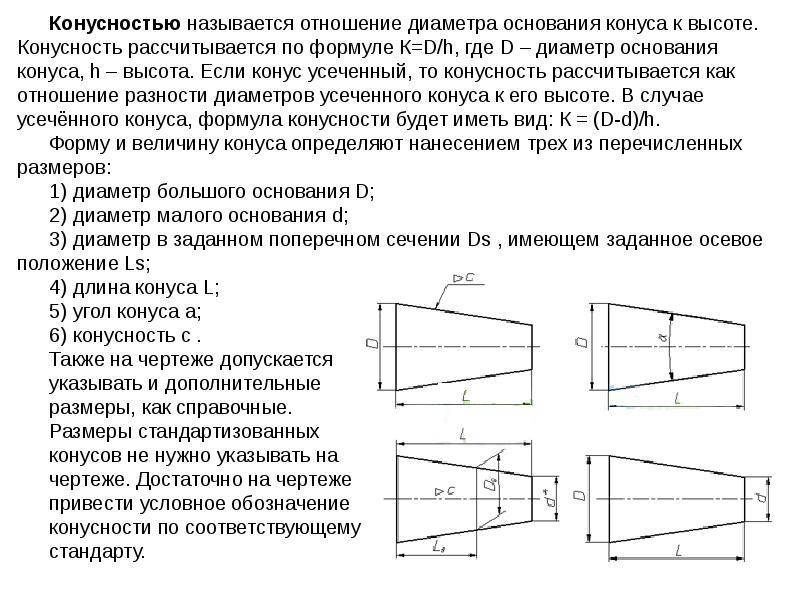
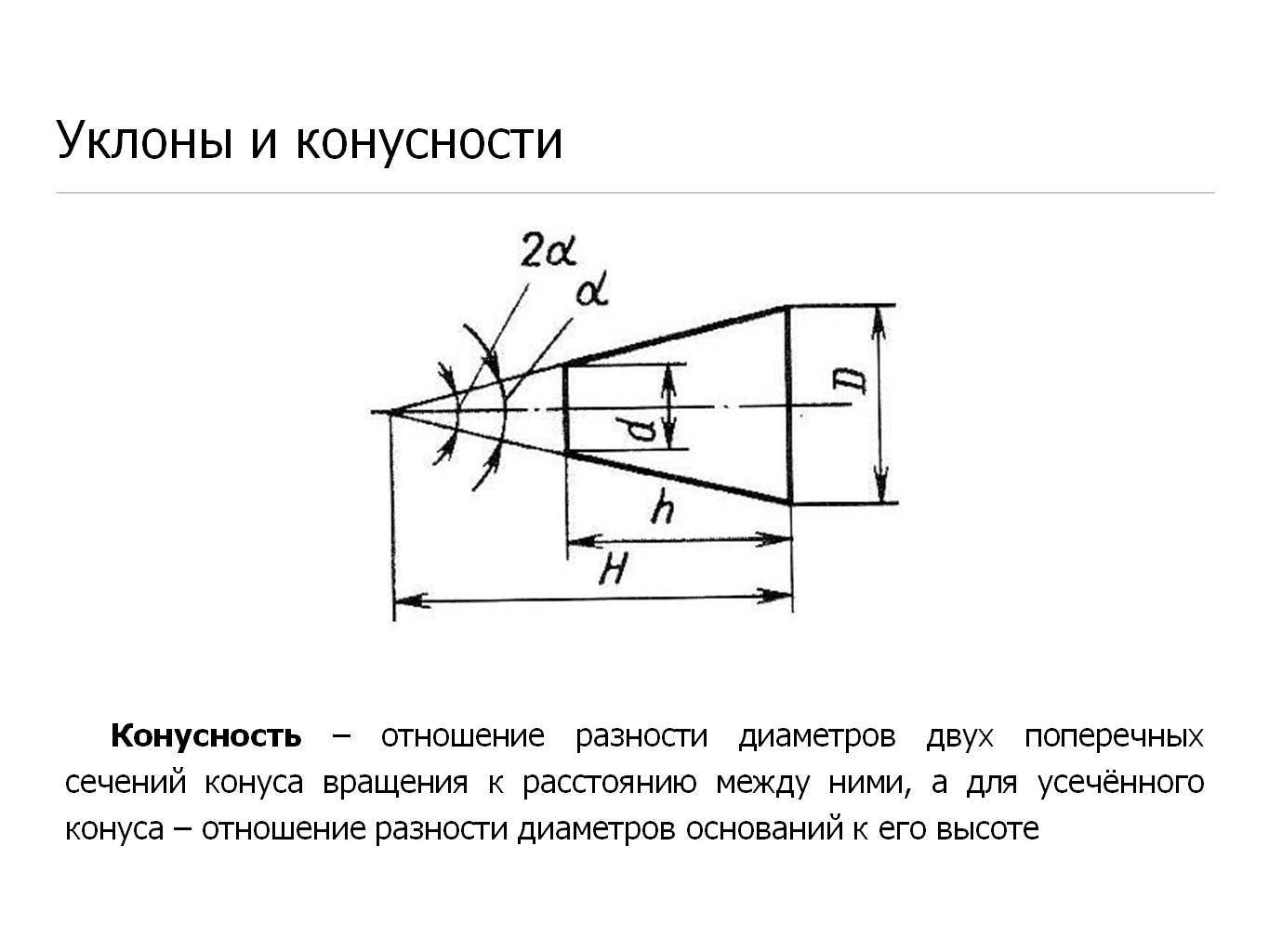
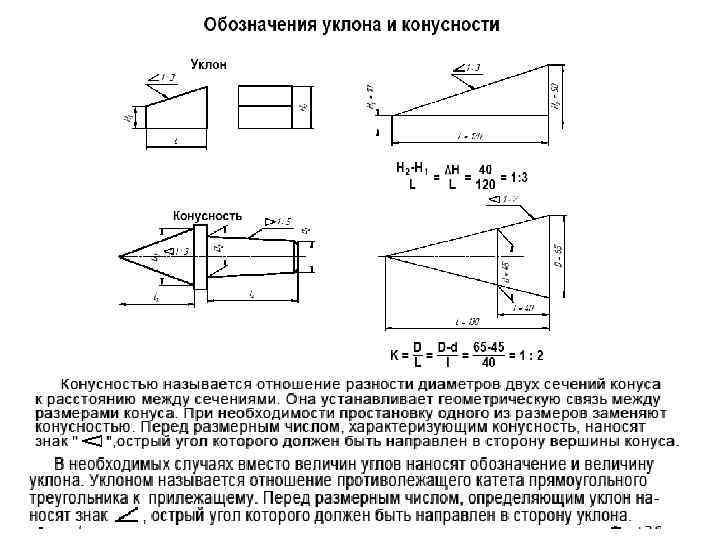
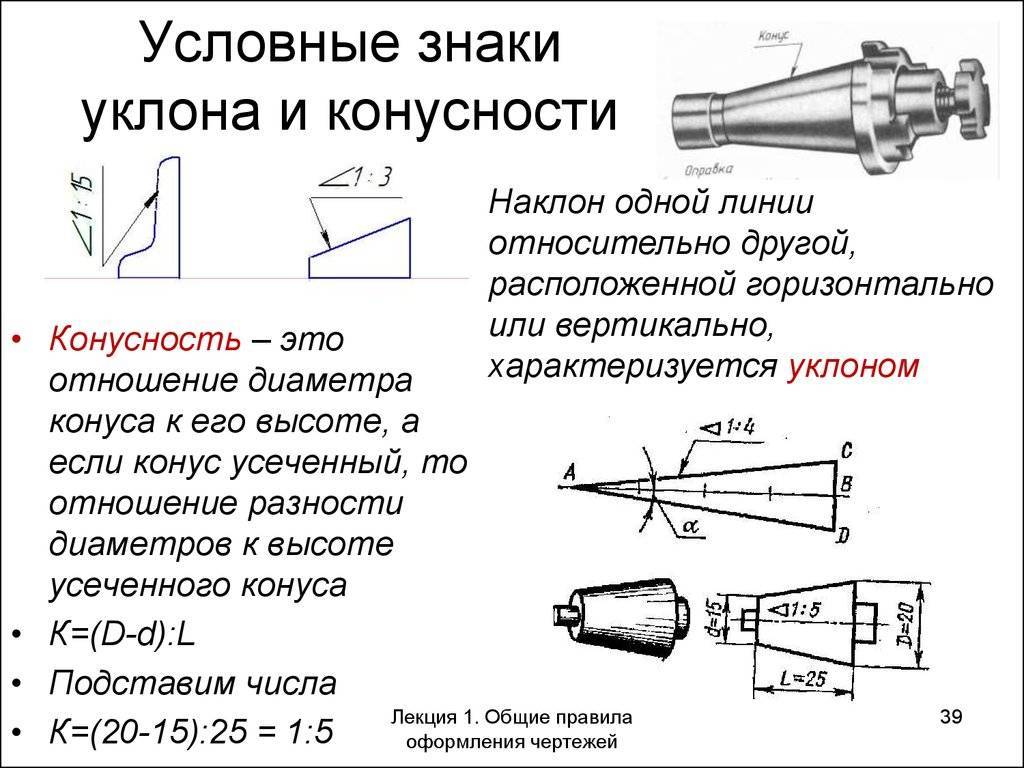
Конусность

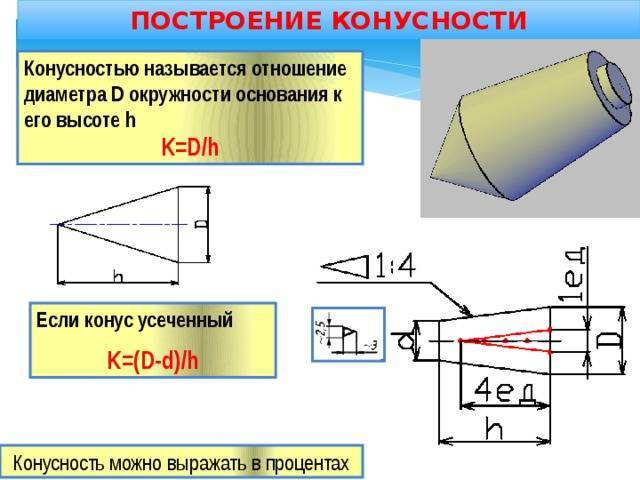
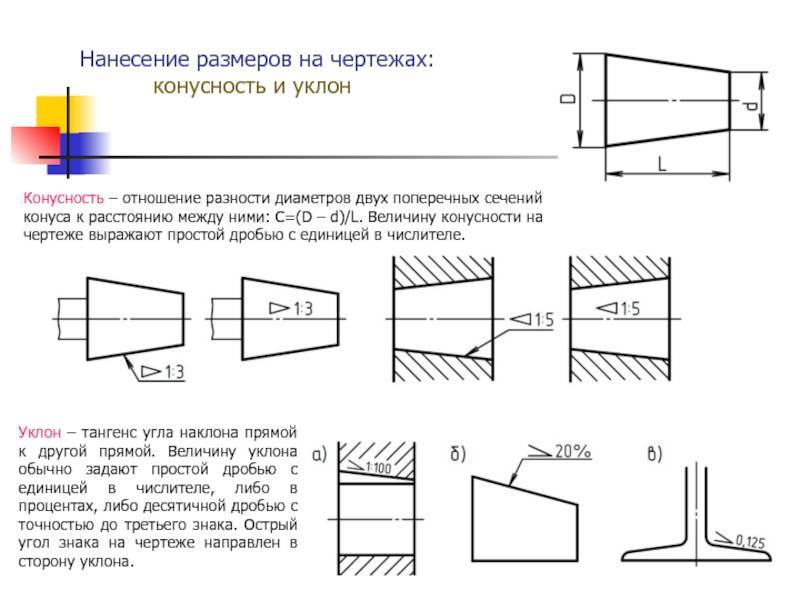
Отношение разности диаметров двух поперечных сечений конуса (D-d.) к расстоянию между ними (l) (рис. 6.39, а) называется конусностью (К): К = (D – d)/l.

Рис. 6.39. Построение конусности и нанесение се величины

Например, конический элемент детали с диаметром большего основания 25 мм, диаметром меньшего основания 15 мм, длиной 50 мм будет иметь конусность К = (D – d)/l = (25 – 15)/50 = 1/5 = 1:5.

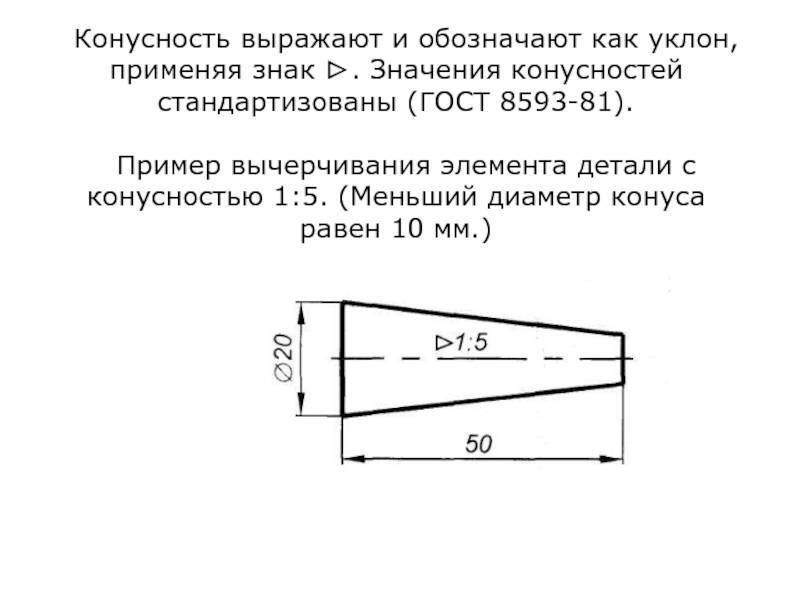
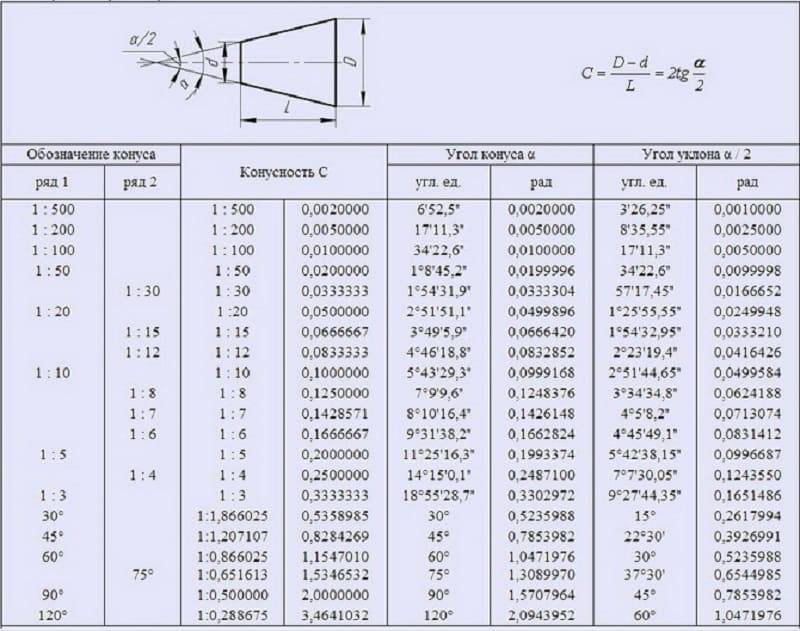
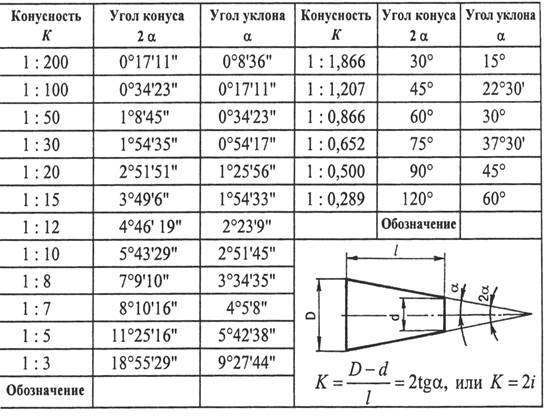
При проектировании новых изделий применяются величины конусности, установленные ГОСТ 8593–81: 1:3; 1:5; 1:7; 1:8; 1:10; 1:12; 1:15; 1:20; 1:30. Стандартизированы также величины конусности, которые имеют элементы деталей с часто встречающимися углами между образующими конуса: углу 30° соответствует конусность 1:1,866; 45° – 1:1,207; 60° – 1:0,866; 75° – 1:0,652; углу 90° – 1:0,5. В чертежах металлорежущих инструментов часто конусность определяется надписью, указывающей номер конуса Морзе. В этих случаях размеры конических элементов устанавливают по ГОСТ 10079–71 и др.

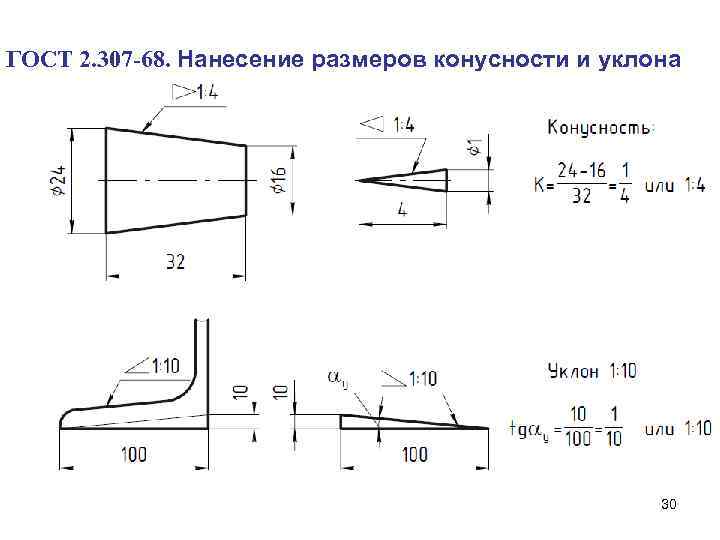
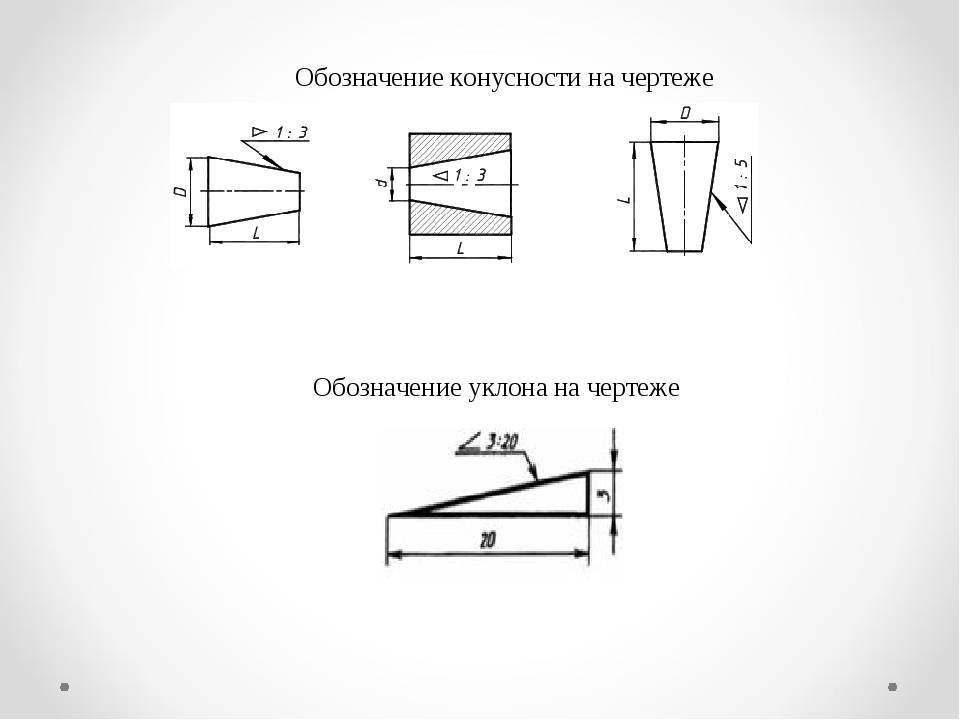
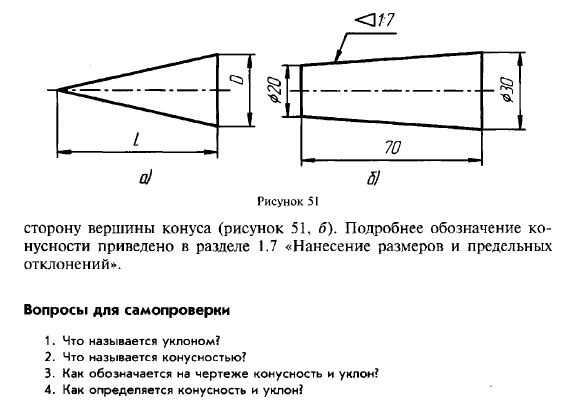
На чертежах конусность наносят согласно правилам ГОСТ 2.307–2011. Перед размерным числом, определяющим величину конусности, наносят условный знак в виде равнобедренного треугольника, острие которого направлено в сторону вершины конуса.

Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно геометрической оси конического элемента.

Они могут быть проставлены над осью (рис. 6.39, 6) или на полке (рис. 6.39, в). В последнем случае полка соединяется с образующей конуса с помощью линии выноски, заканчивающейся стрелкой.

Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.

Рис. 6.40. Определение величины уклона

На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.

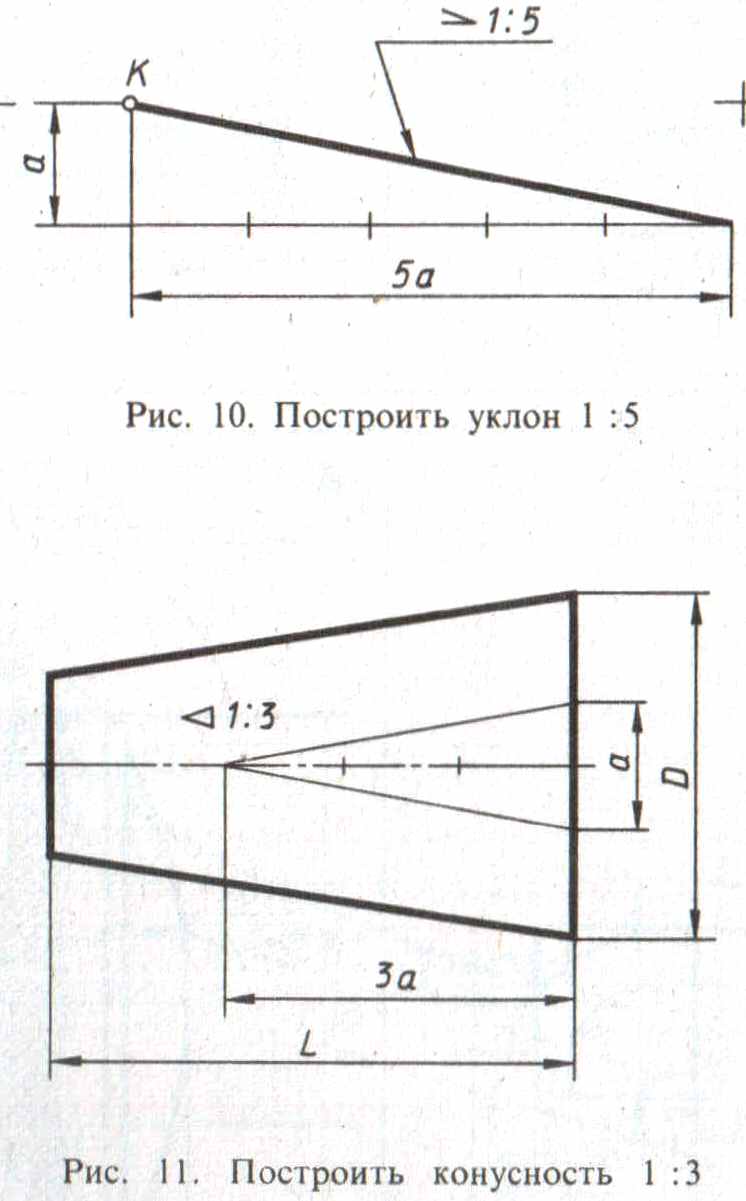
Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).

Рис. 6.41. Построение уклонов и нанесение их величин

При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.

Рис. 6.42. Построение линии по заданному уклону

Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.

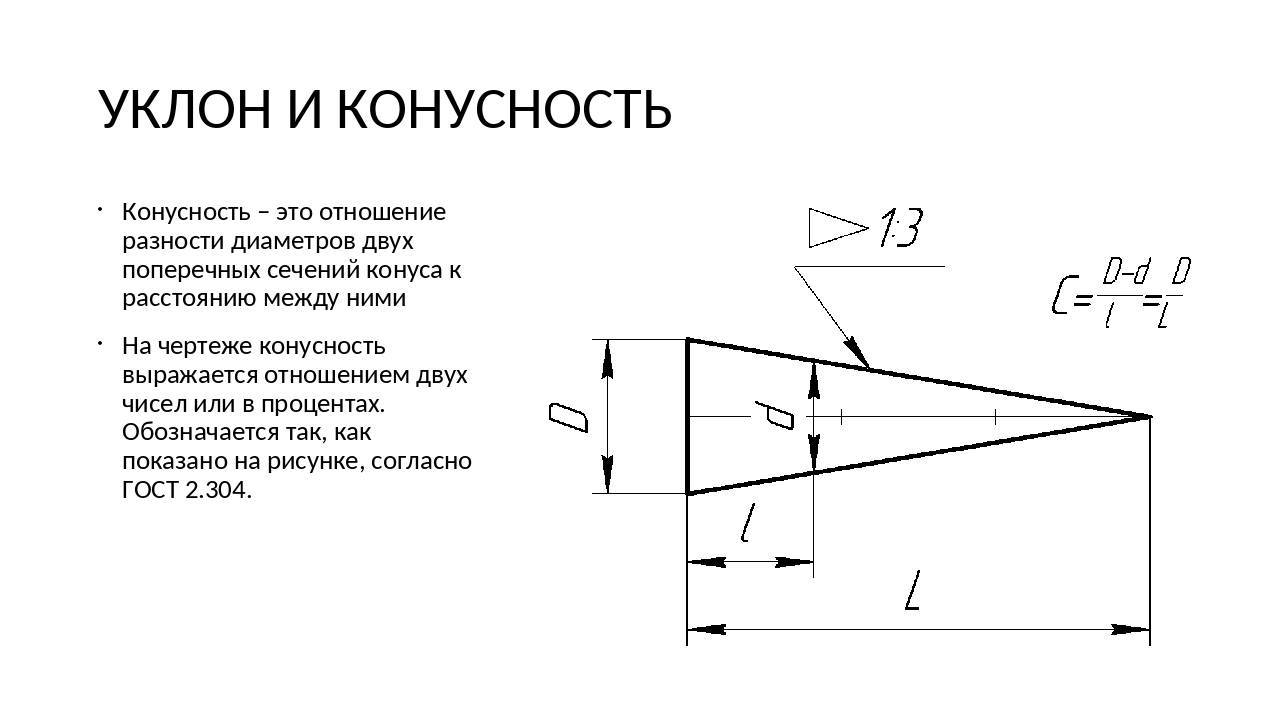
Уклоны и конусность — Техническое черчение

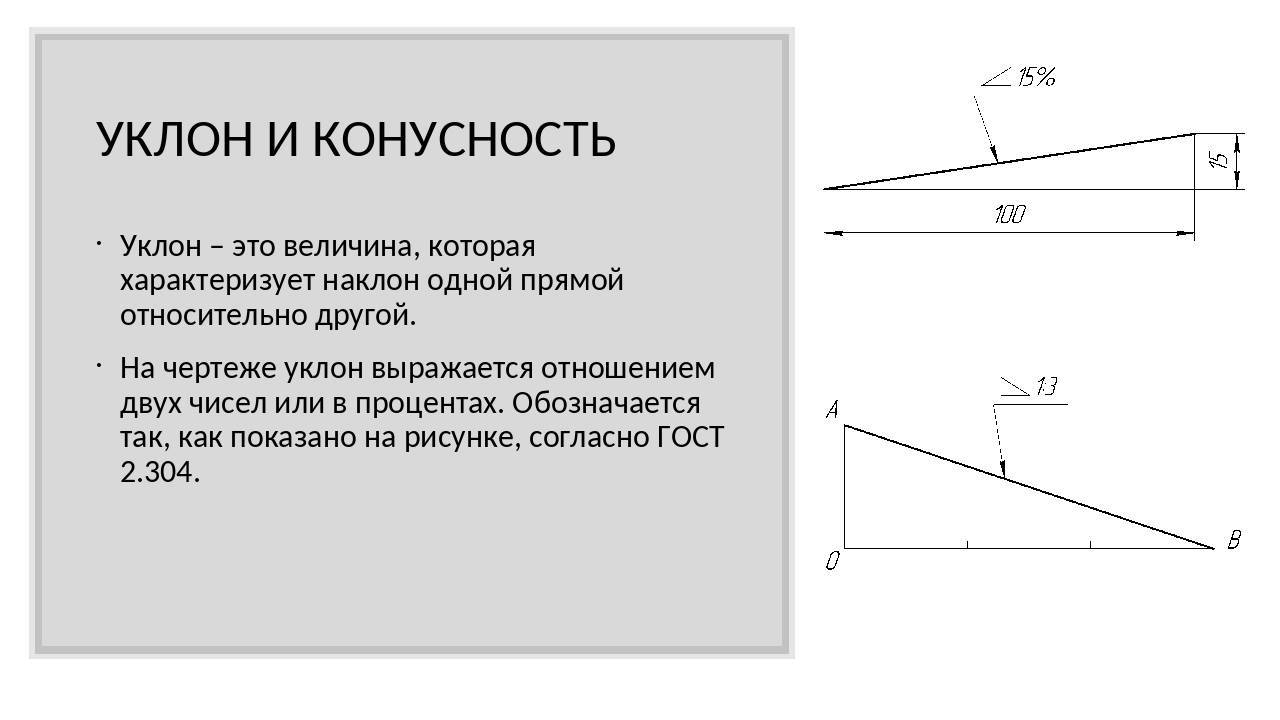
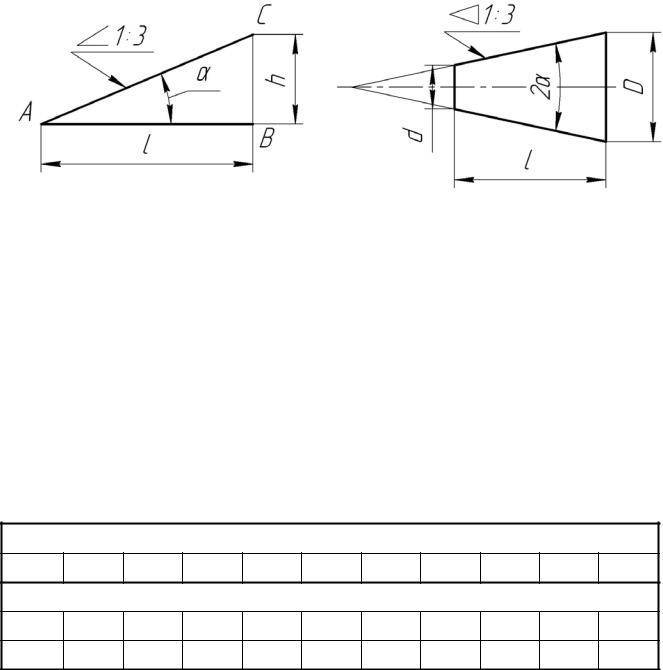
• Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:
• i=AC/AB=tga
• Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)
• k=(D-d)/l=2tga
• Таким образом,
• k = 2i
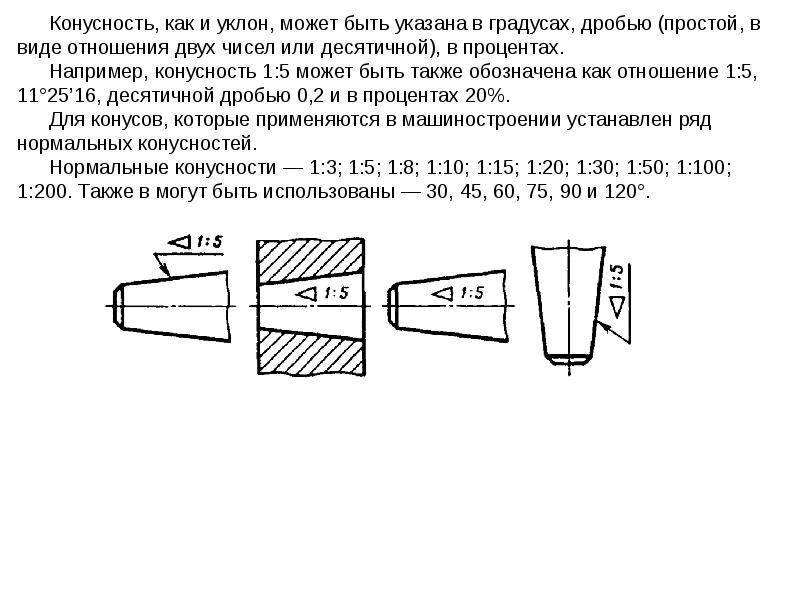
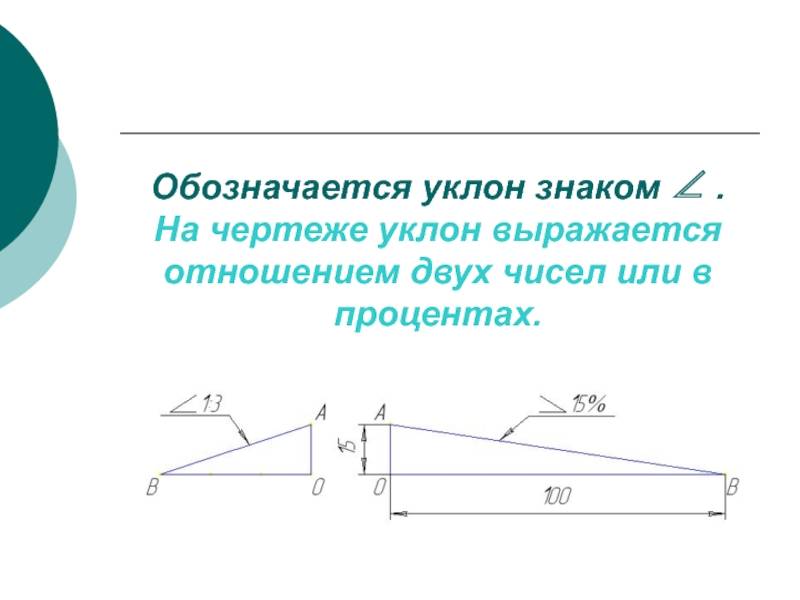
• Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.
• Например: конусность, выраженная в градусах — 11°25’16″; отношением —  1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38″; отношением — 1:10; дробью—0,1; в процентах —  10%.
• Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.
• Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

1. Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):
2. 1)    построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2)    опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм.

Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2.

В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

• Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:
• ps/np=10/100,
• откуда
• ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

1. i=ps/np=1/6
2. где i — заданный уклон.
3. Подставив в формулу числовые значения, получим
4. ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.

ОСНОВНЫЕ РАЗМЕРЫ

2.1. Обозначение размера резьбы, шаги и номинальные значения основных размеров конической (наружной и внутренней) резьбы должны соответствовать указанным на черт.2 и в табл.2.

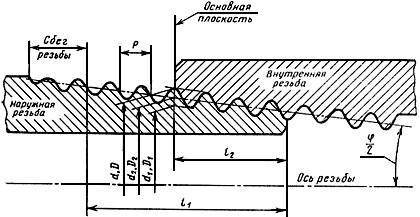
— рабочая длина резьбы; — длина наружной резьбы от торца до основной плоскости

Черт.2

Таблица 2

Размеры в миллиметрах

Обозначение размера резьбы	Шаг	Диаметры резьбы в основной плоскости	Длина резьбы
0,907	7,723	7,142	6,561	6,5	4,0
9,728	9,147	8,566
1,337	13,157	12,301	11,445	9,7	6,0
16,662	15,806	14,950	10,1	6,4
1,814	20,955	19,793	18,631	13,2	8,2
26,441	25,279	24,117	14,5	9,5
1	2,309	33,249	31,770	30,291	16,8	10,4
1	41,910	40,431	38,952	19,1	12,7
1	47,803	46,324	44,845
2	59,614	58,135	56,656	23,4	15,9
2	75,184	73,705	72,226	26,7	17,5
3	87,884	86,405	84,926	29,8	20,6
3	100,330	98,851	97,372	31,4	22,2
4	113,030	111,551	110,072	35,8	25,4
5	138,430	136,951	135,472	40,1	28,6
6	163,830	162,351	160,872

Допускается применять более короткие длины резьб.

2.2. Числовые значения диаметров и вычисляют по следующим формулам

, (1)

. (2)

Числовые значения диаметра установлены эмпирически.

2.3. Разность действительных размеров должна быть не менее разности номинальных размеров и , указанных в табл.2.

2.4. Длина внутренней конической резьбы должна быть не менее 0,8 (, где — в соответствии с табл.3)*. ________________ * Текст документа соответствует оригиналу. — Примечание изготовителя базы данных.

Таблица 3

Размеры в миллиметрах

Обозначение размера резьбы	Смещение основной плоскости резьбы	Предельные отклонения диаметра внутренней цилиндрической резьбы
;	0,9	1,1	±0,071
;	1,3	1,7	±0,104
;	1,8	2,3	±0,142
1; 1; 1; 2	2,3	2,9	±0,180
2; 3; 3; 4; 5; 6	3,5	3,5	±0,217

Примечание. Предельные отклонения и не распространяются на резьбы с длинами, меньшими указанных в табл.2.

2.5. Обозначение размеров резьбы, шаги и номинальные значения наружного, среднего и внутреннего диаметров внутренней цилиндрической резьбы должны соответствовать указанным на черт.3 и в табл.2.

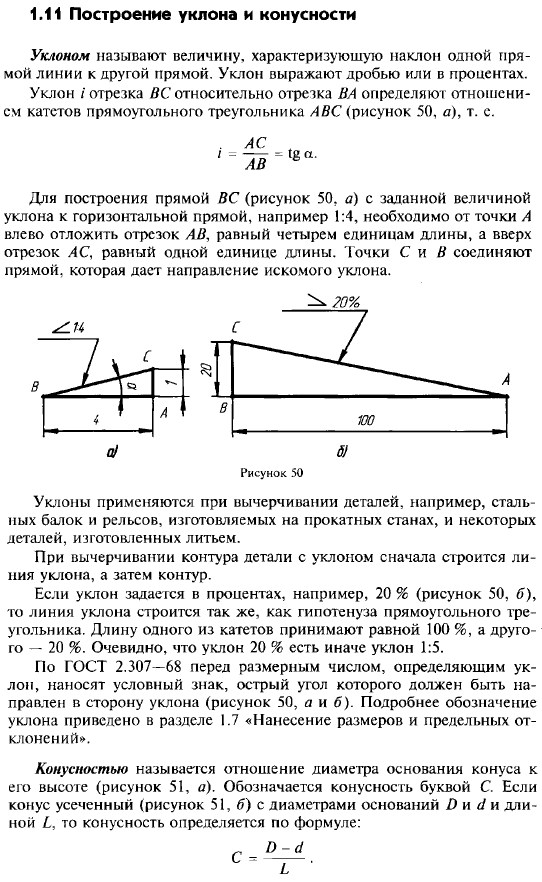
Построение уклона и конусности

Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:

1. Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
2. В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
3. С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.

На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:

1. Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
2. Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
3. Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
4. Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
5. Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.

Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:

1. Программа при построении наклонных линий автоматически отображает угол. Проведенные расчеты в этом случае позволяют проводить построение даже в том случае, если нет информации об большом или малом, промежуточном диаметре. Конечно, требуется информация, касающаяся расположения диаметров относительно друг друга.
2. Есть возможность использовать дополнительные инструменты, к примеру, привязку для построения нормальной конусности. За счет этого существенно прощается поставленная задача и ускоряется сама процедура. При черчении от руки приходится использовать специальные инструменты для контроля подобных параметров.
3. Длина всех линий вводится числовым методом, за счет чего достигается высокая точность. Погрешность может быть допущена исключительно при применении низкокачественного устройства для вывода графической информации.
4. Есть возможность провести замер всех показателей при применении соответствующих инструментов.
5. Для отображения стандартов используются соответствующие инструменты, которые также существенно упрощают поставленную задачу. Если программа имеет соответствующие настройки, то достаточно выбрать требуемый инструмент и указывать то, какие размеры должны быть отображены. При этом нет необходимости знания стандартов, связанных с отображением стрелок и других линий.