Деформация кручения

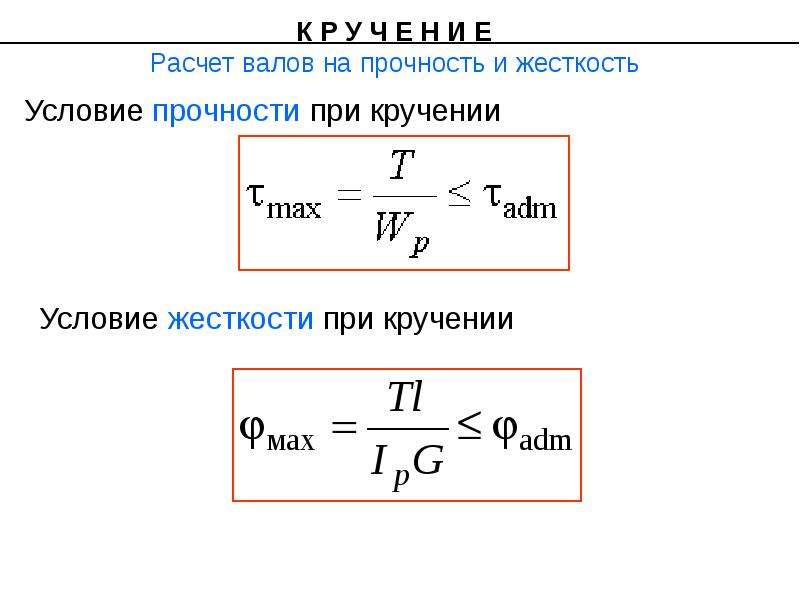
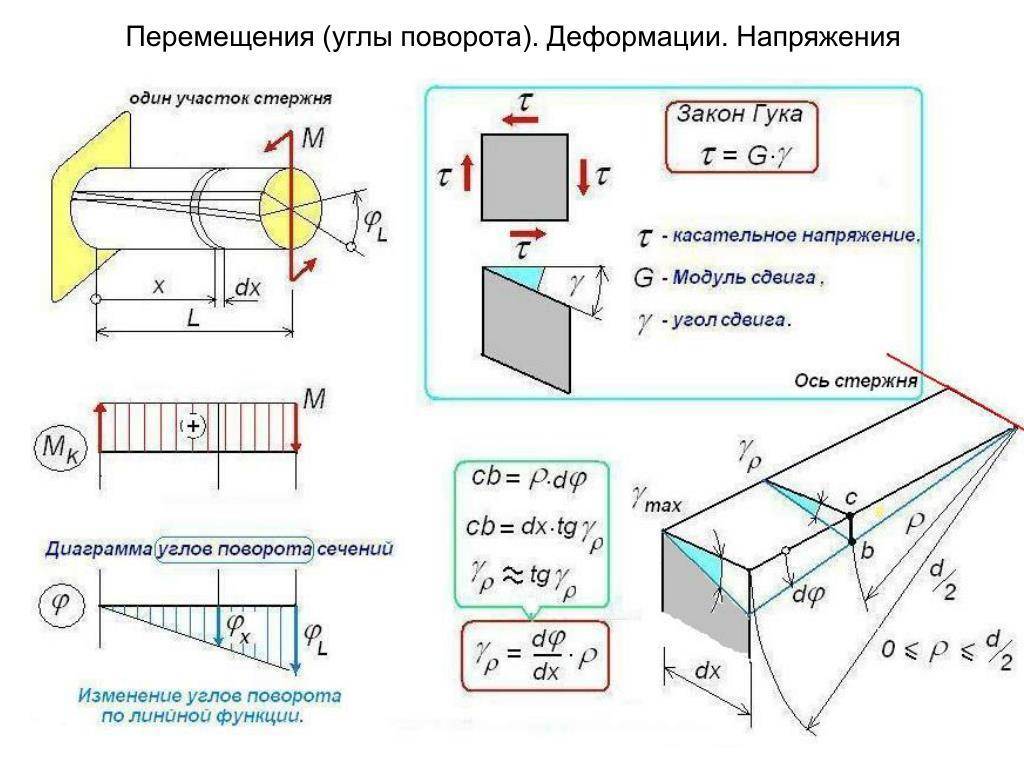
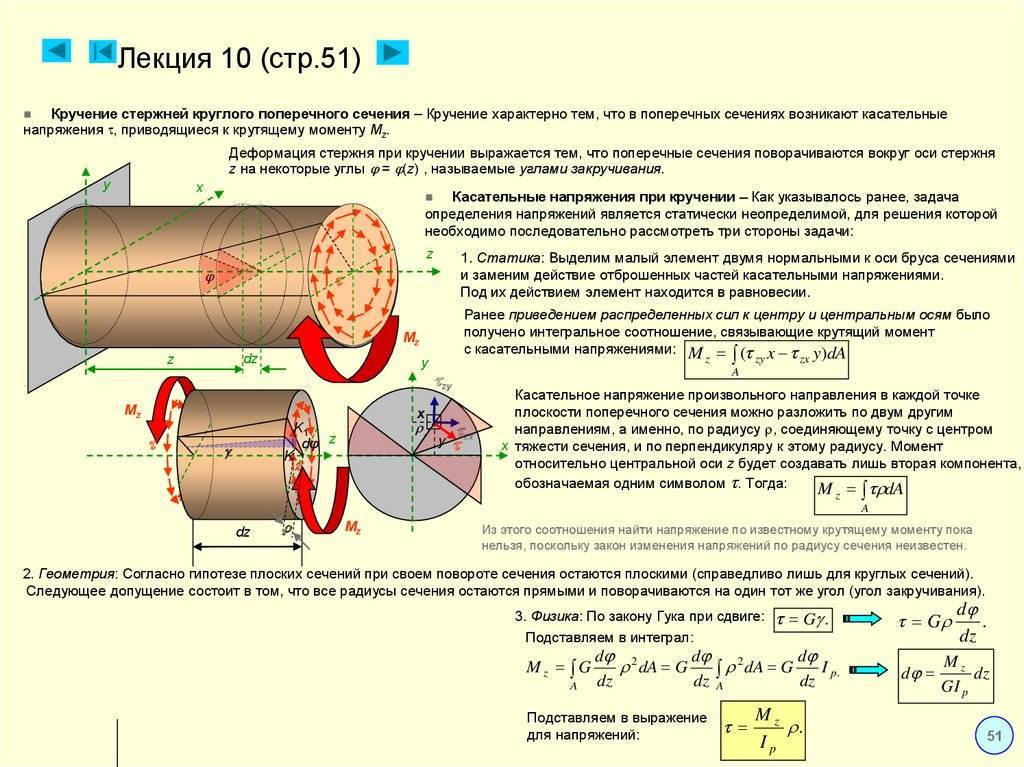
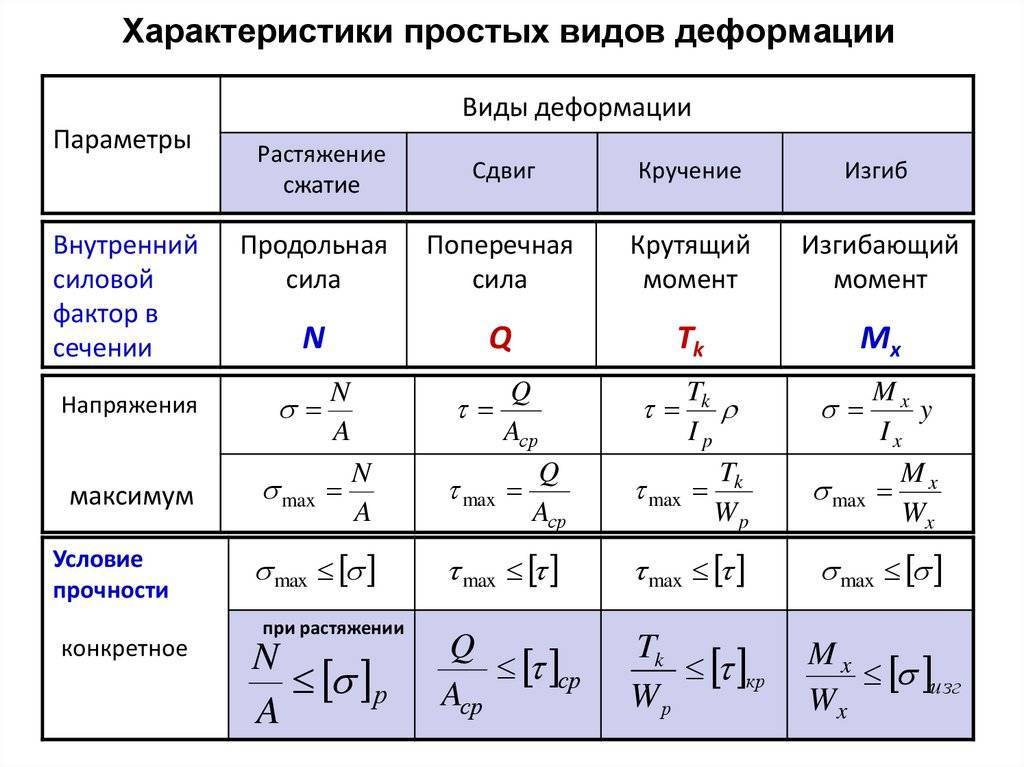
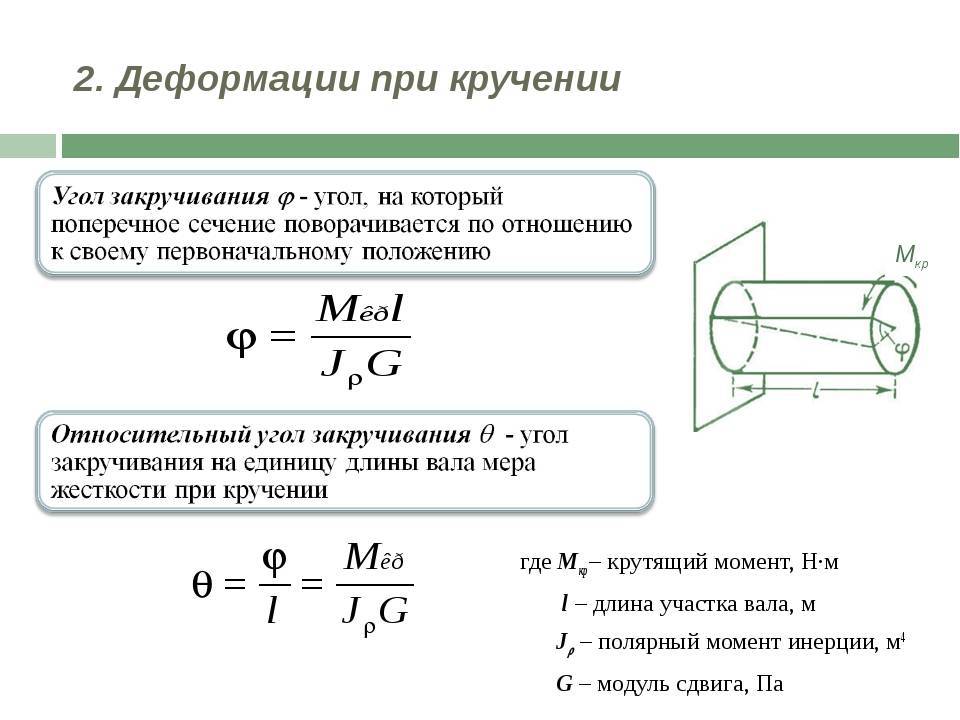
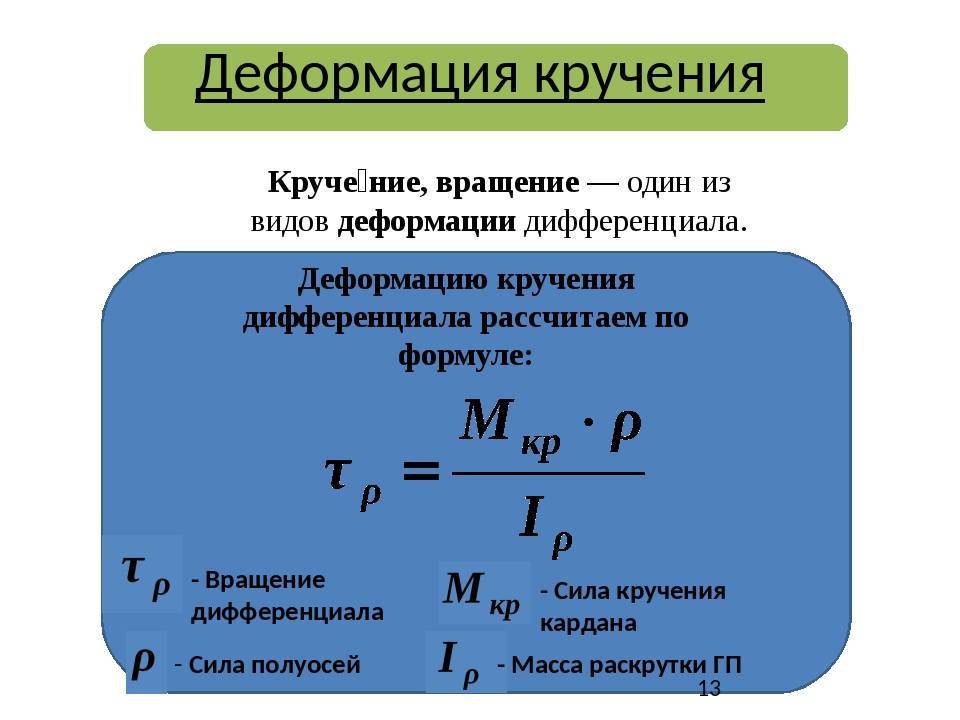
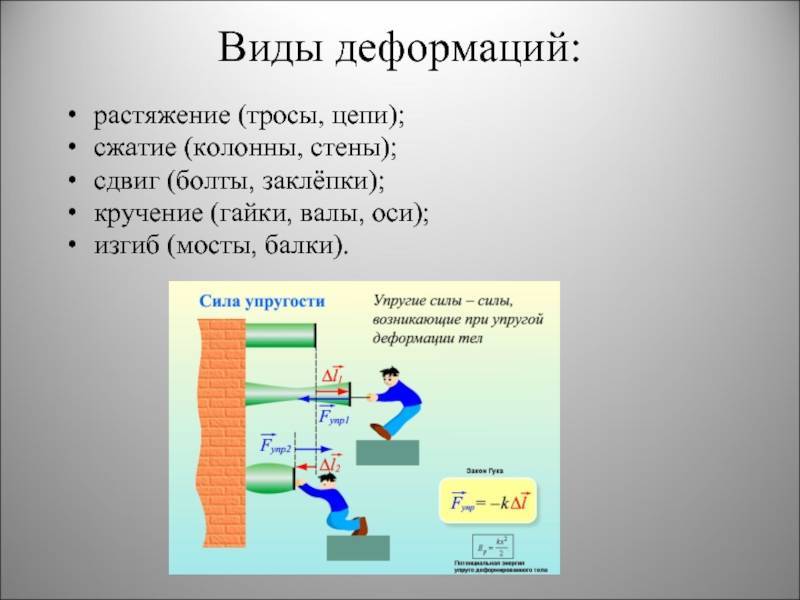
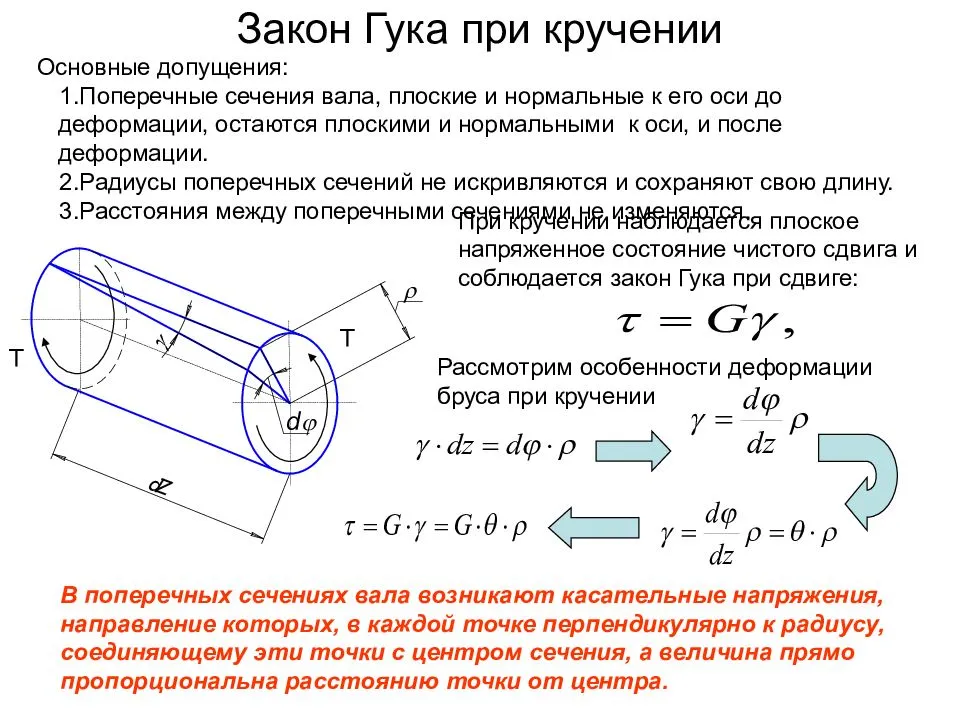
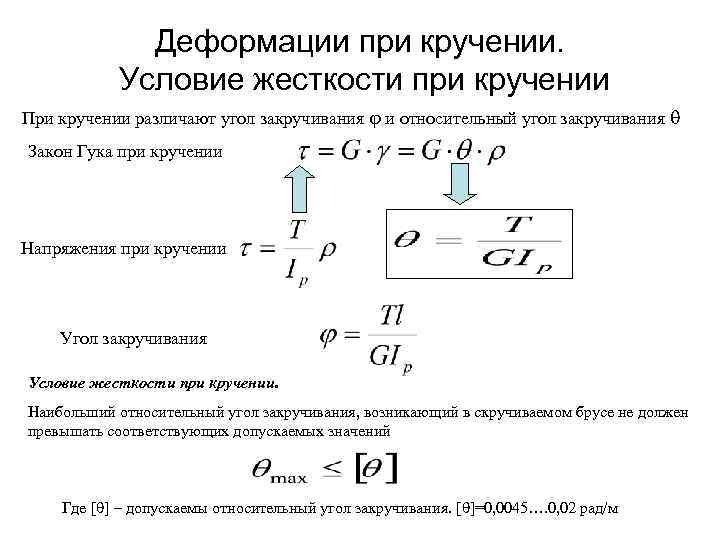
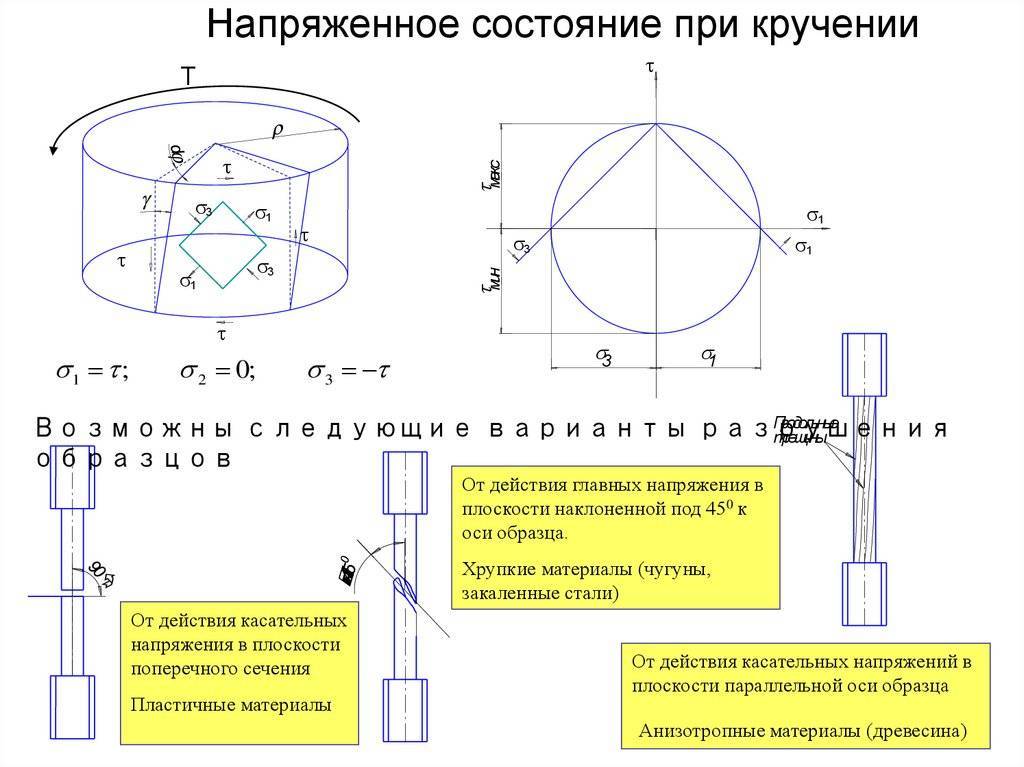
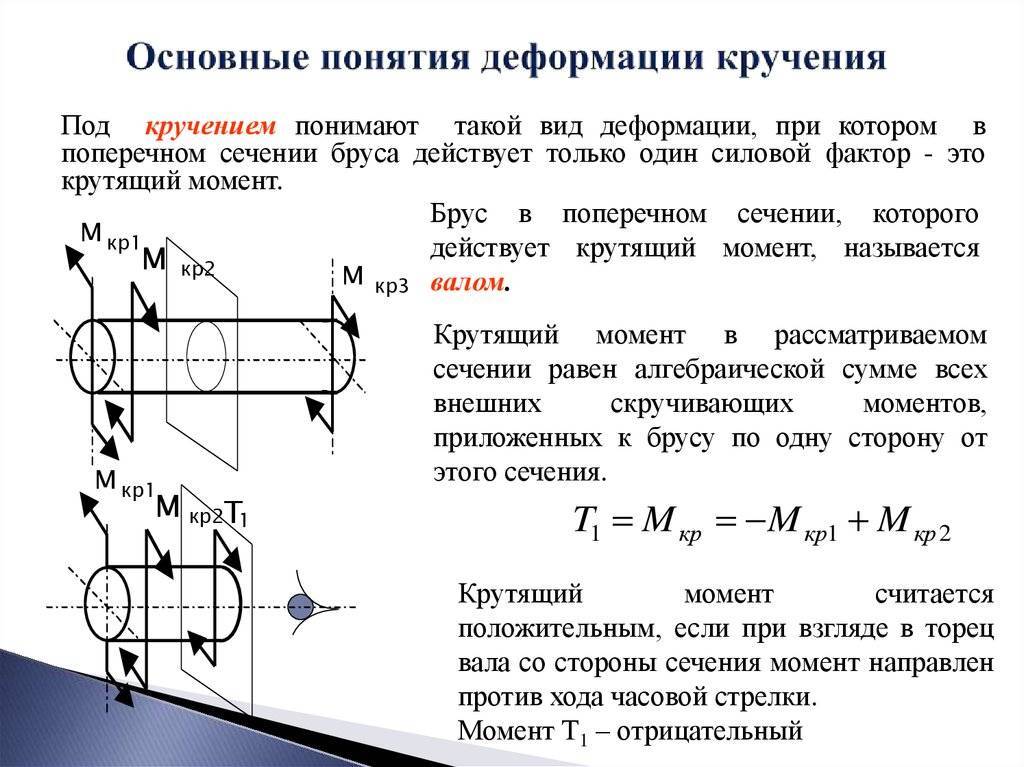
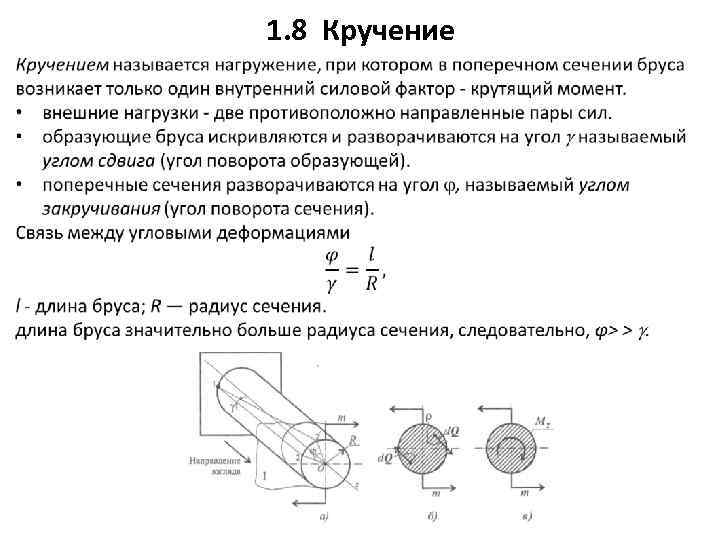
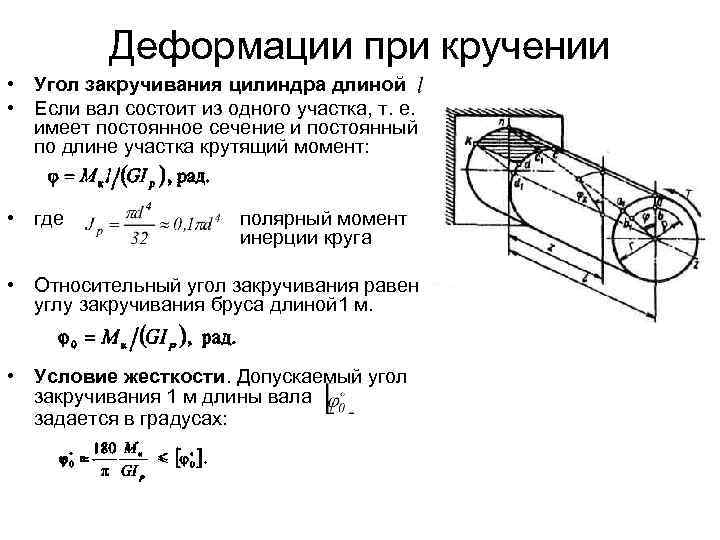
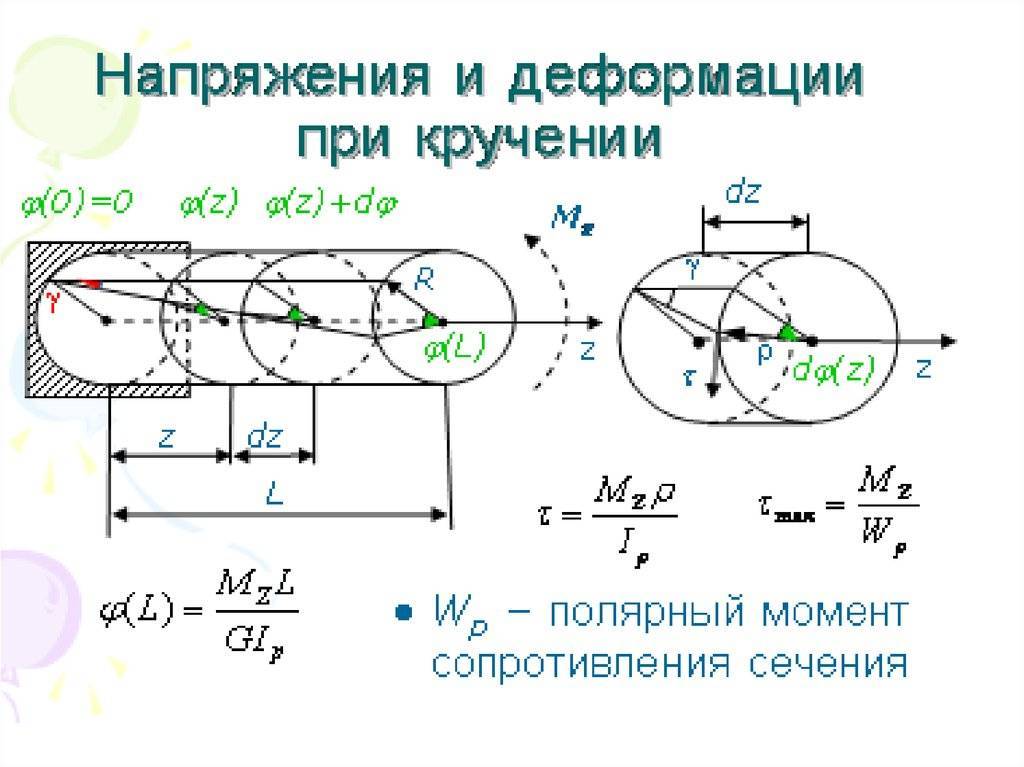
Закон Гука

От чего же зависит сила упругости? Роберт Гук, современник Ньютона, ответил на этот вопрос (рисунок 8).

Рисунок 8. Английский физик и изобретатель Роберт Гук (1635-1703). Установил зависимость силы упругости от деформации тела.

Рассмотрим опыт, изображенный на рисунке 9. 

Рисунок 9. Опыт на определение зависимости силы упругости от деформации тела.

У нас есть штатив, к которому мы прикрепим резиновый шнур. Измерим его длину и обозначим как $l_0$.

Далее подвесим к шнуру чашку с гирей. Шнур удлинится. Снова измерим его длину — теперь она имеет значение $l$.

Шнур изменил свою длину после наших действий. Это изменение (удлинение шнура) мы можем найти по формуле:

$$\Delta l = l- l_0$$

где $\Delta l$ — изменение длины. Знак $\Delta$ (греческая буква “дельта”) используется как символ для обозначения изменения между значениями какой-либо величина.

Если мы будем менять гири на чашке, то будет меняться длина шнура, т.е. его удлинение (деформация) $\Delta l$.

Этот опыт показывает, что

Так мы подошли к закону Гука:

$$F_{упр} = k \Delta l$$

Где $ \Delta l$ — изменение длины тела, $k$ — коэффициент пропорциональности, который называется жесткостью. Жесткость тела зависит от материала, формы и размеров тела.

{"questions":,"explanations":,"answer":}},"hints":[]}]}

Расчеты на прочность и жесткость

Прочность характеризует способность конструкционного материала сопротивляться внешним воздействиям без разрушений и остаточных изменений. Жесткость находится в линейной зависимости от модуля Юнга и размера сечения. Чем больше площадь, модуль упругости не меняется, тем больше жесткость. В общем случае жесткость подразумевает способность деформироваться без значительных изменений. Коэффициент запаса прочности – безразмерная величина, равная отношению предельного напряжения к допустимому. Запас прочности характеризует штатный режим работы конструкции даже с учетом случайных и не предусмотренных нагрузок. Наименьшим запасом прочности обладают пластические (1.2-2.5) и хрупкие (2-5) материалы.

Применение в расчетах этих коэффициентов позволяет, например, рассчитать опасную толщину для стержня, при которой может возникнуть максимальное нормальное напряжение. Используя коэффициент прочности и возможное предельное напряжение возможно произвести расчет необходимого диаметра вала, который гарантированно обеспечит упругую деформацию и не приведет к пластической. Для инженеров-экономистов важны расчеты наименьших безопасных размеров деталей конструкции по заданным нагрузкам.

Большинство практических расчетов на прочность и жесткость производятся для получения минимальных значений геометрических размеров конструкционных элементов и деталей машин в условиях известных внешних воздействий и необходимого и достаточного запаса прочности. Может решаться обратная задача получения значений предельных нагрузок при условии сохранения геометрических размеров и для конкретного материала.

Сложные конструкции могут быть разделены на элементарные части, для которых будут производиться расчеты, затем полученные результаты интерпретируются в рамках всей системы, для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений статически определенной системы.

С помощью известной жесткости материала делают расчеты максимально возможной длины балки или стержня (вала) при условии неизменности его сечения. Для ступенчатых валов необходимо строить эпюры воздействия внешних сил и возникающих в точках их приложения внутренних напряжений в критических точках. От правильно построенной теоретической модели будет зависеть насколько эффективно и долго прослужит вал для станка, не разрушится ли он от динамических крутящих моментов. На этапе проектирования можно выявить потенциальные слабые точки и рассчитать необходимые параметры для заданного предела прочности.

При расчетах соединений используют пределы текучести используемых материалов и коэффициенты запаса прочности, вычисляют максимально возможные напряжения.

Исследования на прочность обычно подразумевают решение нескольких задач: в условиях проведения поверочного расчета на проверку прочности при известных усилиях и площади сечения оценивают фактический коэффициент запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисляют грузоподъемность или несущую способность с помощью определения внутреннего усилия при известной площади сечения и напряжении.

Прочностные расчеты при разных видах воздействий в рамках условно статических систем сложны, требуют учета многих, иногда не очевидных, факторов, их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.

Определение[ | ]

Элемент g

группыG называетсяэлементом кручения , если он имеет конечный порядок, то есть существует натуральноеn , такое чтоgn =e , гдеe обозначат нейтральный элемент группы. Группа называется периодической (илигруппой кручения ), если все её элементы являются элементами кручения, игруппой без кручения , если единственный элемент кручения — нейтральный. Известно, что любая абелева группа является модулем над кольцом целых чисел; в частности, определение элемента кручения для неё можно переформулировать так: существует ненулевое целое число, такое что умножение на это число переводит данный элемент в ноль. Это мотивирует следующее определение:

Элемент m

модуляM над кольцомR называетсяэлементом кручения , если существует ненулевой регулярный элементr кольцаR (то есть элемент, не являющийся левым или правым делителем нуля), аннулирующийm , то есть такой, чтоrm = 0. В случае работы с целостным кольцом предположение регулярности можно отбросить. Аналогичным образом определяются модуль кручения и модуль без кручения. В случае, если кольцоR коммутативно, можество всех элементов кручения модуляM образует подмодуль, называемыйподмодулем кручения (в частности, для модуля надZ он называется подгруппой кручения).

Более общо, пусть M

— модуль над кольцомR иS — мультипликативно замкнутая система кольца. Элементm модуляM называется элементомS-кручения , если существует элемент мультипликативной системы, аннулирующийm . В частности, множество регулярных элементов кольца является наибольшей мультипликативной системой.

Виды деформаций печатных плат

В процессе эксплуатации, печатные платы, как элементы конструкции, испытывают на себе воздействие внешних сил. Результаты их взаимодействия могут приводить к короблению.

Частными случаями данной деформации являются изгиб и кручение материала основания печатной платы.

Ниже, на рисунках 1 и 2 представлены каждый из указанных видов деформаций печатных плат.

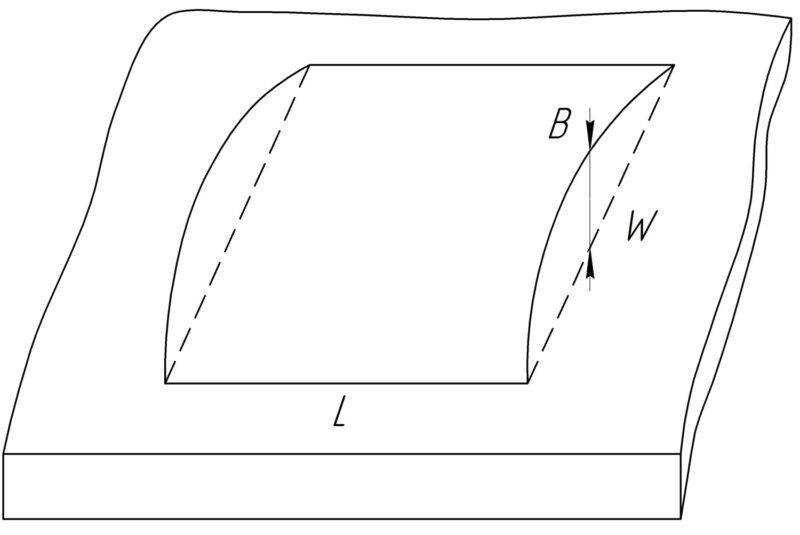Рисунок 1 – деформация изгиба печатной платы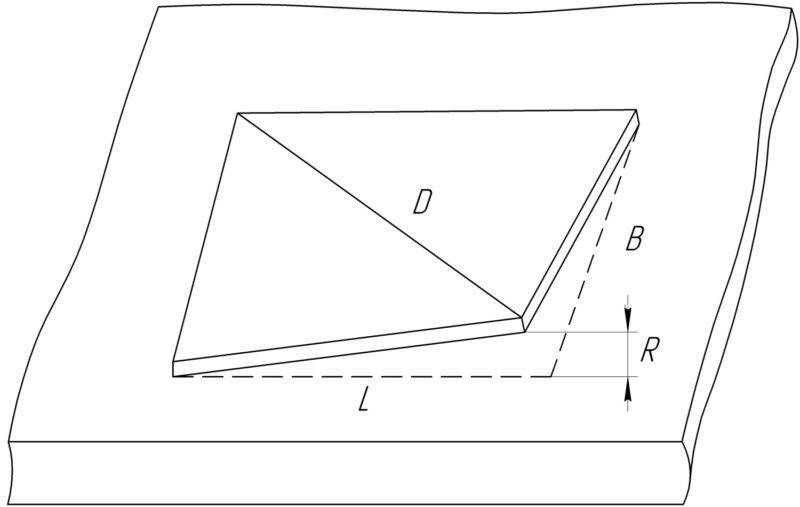Рисунок 2 – Деформация кручения печатной платы

Рассмотренные виды деформаций могут привести к ненадежности конструкции. Поэтому величина изгиба-кручения печатной платы строго регламентируется стандартами.

Стандарты нормирующие величину изгиба-кручения печатных плат

• ГОСТ 23752-79 Платы печатные. Общие технические условия. Отечественный стандарт, регламентирующий величины деформаций печатных плат;
• IPC-A-610F Критерии приемки электронных сборок (Acceptability of Electronic Assemblies). Стандарт Международной Профессиональной Ассоциации (IPC) определяющий допустимые величины изгиба-кручения печатных плат.

Следуя требованиям данных документов, отклонение от идеальной плоскостности должно лежать в определенных пределах. Данные значения называются допустимыми величинами деформаций печатных плат.

В таблице 1 приведены допустимые по ГОСТ 23752-79 величины деформации печатных плат на жестком основании. Данные параметры приведены на каждые 100 мм длины печатной платы.

Например, длина печатной платы равна 355 мм. Тогда нормированная допустимая величина деформации для соответствующей толщины печатной платы умножается на коэффициент 3,55.

Таблица 1 – Допустимые величины деформаций печатных плат в зависимости от количества слоев, материала основания печатной платы и её толщины.

Толщина ПП (мм)	Односторонние (бумага)	Односторонние (стеклотекстолит)	Двусторонние (бумага)	Двусторонние (стеклотекстолит)	Многослойные
1,0…1,5	1,5	0,9	0,9	0,8	0,5
свыше 1,5 до 2,0	1,2	0,8	0,6	0,6	0,1
свыше 2,0	0,9	0,6	0,5	0,5	0,1

Расчет допустимой величины деформации изгиба печатной платы

Согласно IPC ведется для каждой из сторон по формулам:

1. Rl=L*B/100%;
2. Rw=W*B/100%;

где

• L и W – длина и ширина печатной платы (мм);
• B – коэффициент допустимой деформации печатной платы.

Для плат с поверхностным монтажом B равен 0,75%; для всех остальных – 1,5%.

Рекомендуемые файлы

FREE

Учебный план для ИУ3, ИУ4, ИУ5, ИУ6, ИУ7, РК 6, РЛ6, МТ4, МТ8, МТ11, СМ13 Физика FREE

Лекции 2, 6, 8 и 17 Юрасова Н. И. Физика

Ф-65 Физика

М-61 Физика

6.1.16 Физика

6.2.13 Физика

Опора допускает вращение, но устраняет поступательное движение. Возникшую реакцию можно разложить на две составляющие ¾ горизонтальную и вертикальную.

3. Жесткая заделка.

Такое крепление не допускает ни линейных, ни угловых перемещений. Реакция, возникающая раскладывается на вертикальную и горизонтальную и момент защемления (реактивный момент).

7.2. Определение внутренних усилий при изгибе. Правило знаков для изгибающих моментов и поперечных сил.

Для определения внутренних усилий при изгибе (изгибающий момент и поперечная сила) применим метод сечений.

Рассмотрим равновесие левой части.

Взаимодействие внутренних частей заменим внутренними усилиями: изгибающим моментом M_и и поперечной силой Q. Для их определения используем два уравнения равновесия.

1) SY=0; A-F₁+Q=0; Q=S(F_i)_y

2) SM=0; A_z-F₁(Z-Q)-M_и=0

      M_и=Sm(F_c)

Таким образом:

1) Поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих на одну сторону от сечения.

2) Изгибающий момент в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.

Поперечная сила в сечении балки считается положительной; если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа сверху вниз, и отрицательной в противном случае.

Изгибающий момент в сечении mn балки считается

положителным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, справа ¾ против. И отрицательным в противоположном случае.

Есть другое, более удобное для запоминания правило. Изгибающий момент положительный, если в рассматриваемом сечении балка изгибается выпуклостью вниз.

7.3. Построение эпюр изгибающих моментов и поперечных сил.

Рассмотрим пример:

Построить эпюры M_и и Q для балки на рис.

Проводим сечения Z₁ и Z₂. Изгибающий момент определим, взяв сумму моментов внешних сил справа от сечения

M_и=0

В сечении II-II

MZ₂=-F(Z₂ – a₂)

Знак минус потому что балка изгибается выпуклостью вверх.

Получили уравнение прямой

M_z2 = a₂ = 0

M_z2 = a₁ + a₂ = -F_a1                                          M_max=-F_a1 возникает у места заделки

Вычислим поперечную силу в сечении I-I. Проектируя на оси силы справа от сечения получим Q_z1=0. Тем же путем Q_z2=+F. Знак плюс взят т.к. внешняя сила справа от сечения направлена сверху вниз.

7.4. Определение нормальных напряжений. Условия прочности по нормальным напряжениям.

При деформации балки большие деформации испытывают более удаленные от нейтрального слой. Это слой, не испытывающий при изгибе ни растяжения ни сжатия.

Относительное удлинение волокна

e = Z / r

Z ¾ расстояние от нейтральной оси до рассматриваемого волокна.

r ¾ радиус кривизны нейтрального слоя

Тогда по закону Гука

s = Ee = E(Z / r)                     (1)

Можно также записать

M_и = EI_у / r,

где I_у = ò_AZ2dA ¾ представляет момент инерции сечения относительно нейтральной оси y. Откуда

1 / r = M_и / EI_у                                    (2)

K = 1 / r ¾ кривизна нейтрального слоя, т.е. кривизна оси балки при изгибе прямо пропорционально изгибающему моменту n и обратно пропорционально жесткости (Ei_у) балки. Подставляя (2) в (1) получим:

s = Z M_и / EI_у

Для обеспечения прочности балки необходимо, чтобы наибольшие растягивающие и наибольшие сжимающие напряжения при исгибе в опасном сечении не превосходили допускаемых.

Обозначив h_р и  h_с ¾ расстояния до наиболее удаленных растянутого и сжатого волокна запишем:

max s_р = M_иh_р / EI_у

max s_с = M_иh_с / EI_у

Для хрупких материалов допускаемые напряжения [s_с] > [s_р] в 3-5 раз. Поэтому для балок применяют сечения не симметричные относительно нейтральной оси. В указанном случае надо составлять два условия прочности:

max s_р = M_и / W_ур £ [s_р]

max s_с = M_и / W_ус < [s_с]

при симметричном сечении балки

s = (M_и / I_у)(h / 2) £

W_у = 2I_у / h ¾ осевой момент сопротивления.

Момент сопротивления является геометричесой характеристикой поперечного сечения балки, определяющей прочность при изгибе.

Значения W_у для простейших случаев:

а) прямоугольник

W_x = 2I_x / h = bh2 / 6

б) круг

W_x = 2I_x / d = pd42 / 64d = pd3 / 32 » 0,1d3

в) для кольца

W_x = (pD3 / 32) / (1-c4) = 0,1D3(1-c4)

Допускаемый изгибающий момент определяется

[M_и] £ W_x

7.5. Рациональные формы сечения балок.

Рекомендация для Вас – 4.4. Контроль за выполнением производственной программы.

Для количественной оценки рациональности сечения (при замере материала) служит безразмерная величина

w_x = W_x / ÖA3

это осевой удельный момент сопротивления. w_x зависит только от формы сечения

круг w_x  = 0,14

двутавр w_x  = 1,02-1,51

Контрольные вопросы

1. Выведите формулу (2).
2. При определении модуля сдвига статическим способом зависимость рекомендуется снять как при возрастающих, так и при убывающих значениях М

   . Почему? Совпадут ли оба полученные таким образом результаты, если трение в осях блоковБ будет значительным?

3. При определении модуля сдвига динамическим способом указывалось, что период колебаний не зависит от амплитуды только при сравнительно небольших значениях последней. Объясните качественно, как будет меняться период при возрастании амплитуды?
4. Какому методу определения G

   вы отдадите предпочтение на практике, статическому или динамическому?

5. Как при динамическом определении G

   измерить величиныL1 иL2 ? Имеет ли смысл выбирать их малыми?

6. Как оценить ошибку измерений по графику зависимости Т2

   отL2 ?

Деформация сдвига. Относительный сдвиг. Модуль сдвига. Тангенциальное напряжение

Деформация сдвига. Деформация сжатия аналогична рассмотренной деформации растяжения. Силы, деформирующие брус при сжатии, направлены вдоль оси бруса, но навстречу друг другу. Величина действительных напряжений при сжатии σсж=N:F, где N — равнодействующая внутренних сил упругости (продольная сила).

Угол γ, на который изменился прямой угол параллелепипеда, назы­вается относительным сдвигом и яв­ляется мерой сдвига, т.е. относительный сдвиг — есть отношение абсолютного сдвига к расстоянию между рассматриваемыми сдвигаемыми сечениями.

Модуль сдвига — физическая величина, характеризующая способность материала сопротивляться сдвиговой деформации.

F — площадь, на которую действует сила; A{\displaystyle \gamma _{xy}=\Delta x/I=tg\theta }aA — сдвиговая деформация; {\displaystyle \Delta x} — смещение; {\displaystyle I}LLlll — начальная длина.

Величина, равная отношению силы к величине поверхности, на которую сила действует, называется напряжением. Если сила направлена по нормали к поверхности, напряжение называется нормальным. Если сила направлена по касательной к поверхности, на которую она действует, напряжение называется тангенциальным. Нормальное напряжение принято обозначать буквой σ, тангенциальное — буквой τ.

Где S-площадь соответствующей грани, f-сила

Силы трения. Движение по наклонной плоскости. Ускорение

Силой трения называют силу, которая возникает при движении одного тела по поверхности другого. Она всегда направлена противоположно направлению движения. Сила трения прямо пропорциональна силе нормального давления на трущиеся поверхности и зависит от свойств этих поверхностей.

При выполнении изучения движения бруска по наклонной плоскости можно выбирать коэффициент трения μ, массу бруска M, угол наклона плоскости α, а также модуль и направление внешней силы. Приводится график зависимости силы сухого трения от относительной скорости соприкасающихся тел, на котором указан вертикальный отрезок, соответствующий трению покоя. При выбранных параметрах эксперимента точкой на графике отмечено реализуемое значение силы трения покоя. Скольжение бруска по наклонной плоскости возможно только в том случае, если сила трения покоя досигает максимального значения (Fтр)max:

Эти силы принято называть силой трения скольжения. Ускорение, которое при этом условии приобретает брусок при скольжении по наклонной плоскости, определяется из второго закона Ньютона

При a < 0 брусок начинает двигаться вверх по наклонной плоскости (из-за наличия внешней силы). В этом случае сила трения скольжения изменяет знак на противоположный.

Если внешняя сила отсутствует, то максимальный угол αmax наклона плоскости, при котором брусок еще удерживается неподвижно силой трения покоя, определяется соотношением:

На практике это соотношение используется для измерения коэффициента сухого трения.

Ускоре́ние (обычно обозначается латинскими буквами a (от лат. acceleratio) или w) — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости {\displaystyle {\vec {v}}}тела при его движении за единицу времени:

{\displaystyle {\vec {a}}={d{\vec {v}} \over dt}.}

Измерение деформации

При проектировании и эксплуатации различных механизмов, технических объектов, зданий, мостов и других инженерных сооружений очень важно знать величину деформации материалов. Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами

Для этого используют приборы, называемые тензометрами

Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами.

Тензометр состоит из тензометрического датчика и индикаторов. В него также может быть включено регистрирующее устройство.

В зависимости от принципа действия тензометры бывают оптические, пневматические, акустические, электрические и рентгеновские.

В основу оптических тензометров положено измерение деформации нити из оптоволокна, приклеенной к объекту исследования. Пневматические тензометры фиксируют изменение давления при деформации. В акустических тензометрах с помощью пьезоэлектрических датчиков проводятся измерения величин, на которые изменяются скорость звука и акустическое затухание при деформации. Электрические тензометры вычисляют деформацию на основе изменений электрического сопротивления. Рентгеновские определяют изменение межатомных расстояний в кристаллической решётке исследуемых металлов.

Вплоть до 80-х годов ХХ века сигналы датчиков регистрировались самописцами на обыкновенной бумажной ленте. Но когда появились компьютеры и начали бурно развиваться современные технологии, стало возможным наблюдать деформации на экранах мониторов и даже подавать управляющие сигналы, позволяющие изменить режим работы тестируемых объектов.

Напряжения и деформации при кручении бруса круглого поперечного сечения

Главная Учебные курсы Сопротивление материалов Кручение Напряжения и деформации при кручении бруса круглого поперечного сечения

Под действием внешнего скручивающего момента, приложенного на правом конце вала (рис. 7.2), левый конец которого жестко закреплен, стержень будет закручиваться. При этом любое сечение стержня, оставаясь плоским, будет поворачиваться на некоторый угол φ

к, называемый углом закручивания. Этот угол изменяется по длине вала от нуля в заделке до максимального на правом конце вала. При этом образующая внешней цилиндрической поверхности вала повернется на уголγ , называемый углом сдвига. Этот угол изменяется вдоль радиуса сечения от нуля на оси вала до —γmax на внешней поверхности. Опыт показывает, что после закручивания бруса круглого сечения поперечные линии, нанесенные на его поверхности, остаются плоскими, а диаметры сечений и расстояния между ними не изменяются. При этом прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных сечениях бруса, а по закону парности касательных напряжений – и в продольных его сечениях, то есть напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. На основании опыта вводятся следующие гипотезы:

1. Нормальные напряжения в поперечных сечениях отсутствуют (иначе изменялись бы расстояния между сечениями).
2. Поперечные сечения при кручении остаются плоскими.
3. Радиусы в поперечных сечениях остаются прямолинейными (не искривляются).

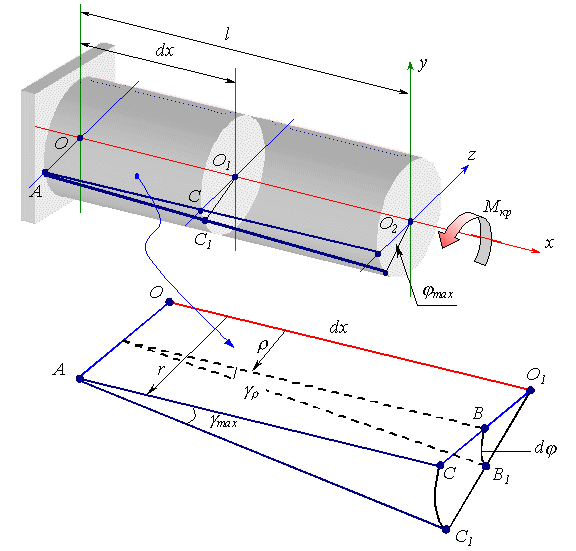
Рис. 7.2.

С учетом указанных гипотез геометрическая картина деформаций вала представлена на рис. 7.2. Рассмотрим, вырезанный из вала клиновидный элемент (см. рис. 7.2) длиной dx

. Из рисунка видно, что

,

(7.2)

откуда следует, что угол сдвига изменяется по радиусу вала по линейному закону.

Согласно закону Гука при сдвиге (3.34), имеем:

откуда получаем:

,

(7.3)

что касательные напряжения в сечении вала изменяются по радиусу по линейному закону.

При чистом кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей – крутящему моменту относительно нормальной к сечению оси. Касательные напряжения перпендикулярны радиусам, проведенным через точки их действия (рис. 7.3).

Рис. 7.3.

Для доказательства этого будем исходить от противного, то есть, предположим, что касательное напряжение не перпендикулярно радиусу. Это означает, что в каждой точке сечения, кроме касательных напряжений, перпендикулярных радиусам, действуют радиально направленные касательные напряжения. Но если это так, то по закону парности и на цилиндрической поверхности радиуса ρ

илиr будет действовать касательное напряжение, что неверно, так как на боковой поверхности нет напряжений.

Крутящий момент в сечении бруса определяется из уравнения (3.5):

или в более краткой записи

,

(7.4)

где ρ

— плечо элементарной касательной силыτ

,

(7.5)

где — есть полярный момент инерции сечения. С учетом уравнения (7.3) можно определить касательное напряжение в произвольной точке

поперечного сечения вала, определяемой радиусомρ :

,

(7.6)

а также максимальное касательное напряжение, действующее на контуре вала:

,

(7.7)

где Wp

— полярный момент сопротивления.

Эпюра распределения касательных напряжений по радиусу показана на рисунке 7.4 для сплошного и полого валов.

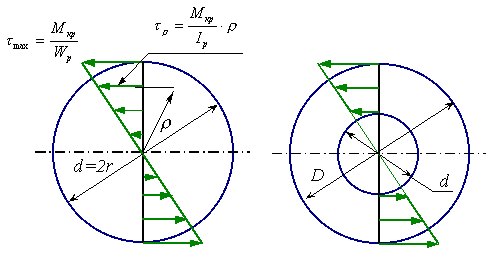
Рис. 7.4.

Угол закручивания вала нетрудно определить на основе полученного выше уравнения:

,

из которого с учетом (7.6) имеем:

.

(7.8)

Угол закручивания всего бруса

.

(7.9)

Если брус имеет несколько участков с различными аналитическими выражениями для Мкр

или различными выражениямиIp , то

.

(7.10)

В частном случае при Мкр(x)=const

илиIp=const , то есть только для бруса постоянного сечения, нагруженного по концам сосредоточенными парами,

.

(7.11)

Предыдущая Напряжения и деформации при кручении бруса круглого поперечного сечения

Следующая

Версия для печати

Кручение

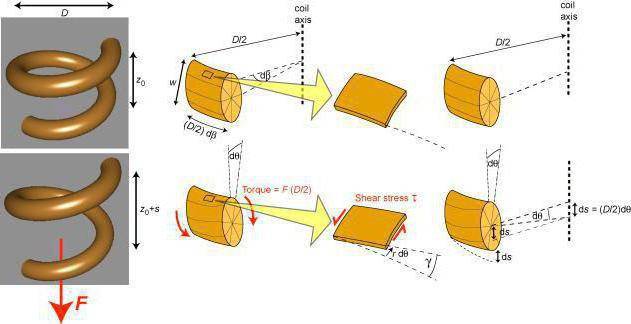
Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Деформацию кручения можно наблюдать, если на стержень, один конец которого закреплен, действует пара сил, лежащих в плоскости, перпендикулярной оси стержня. При кручении отдельные слои тела остаются параллельными, но поворачиваются друг относительно друга на некоторый угол. Деформация кручения представляет собой неравномерный сдвиг. Деформации кручения возникают при завинчивании гаек, при работе валов машин.

Пример деформации кручения цилиндрического стержня

Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ – угол кручения (рис. 1; 2).

Рис. 1.

Отношение угла закручивания φ к длине называют относительным углом закручивания

Закон Гука для малых деформаций кручения выражается формулой

M = Gкр.j

где Gкр.– модуль кручения.

Модуль кручения , помимо материала, зависит также от формы и размеров тела.

Представьте, перед вами цилиндр (или проволока). Если вы начнёте его (её) верхний конец поворачивать вдоль оси, закрепив нижний конец, то при повороте верхней грани на один радиан вы прикладываете вращающий момент, в точности равный модулю кручения (рис.1; 2). Это и есть его определение.

Модуль кручения Gкр показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.

Рис. 2.

Деформация кручения является частным случаем деформации сдвига.

Сдвиг

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 3).

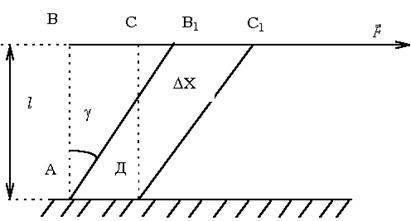
Рис. 3.

Деформация сдвига возникает под действием сил, приложенных к двум противоположным граням тела так, как показано на рисунках 3; 4. Эти силы вызывают смещение слоев тела, параллельных направлению сил. Расстояние между слоями не изменяется. Любой прямоугольный параллелепипед, мысленно выделенный в теле, превращается в наклонный.

Рис. 4.

Мерой деформации сдвига является угол сдвига γ — угол наклона вертикальных граней (рис. 5).

Рис. 5.

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно.

Так как угол мал, формулу можно записать в виде:

где СС1 = D X — абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг γ пропорционален касательному напряжению τ = F/S, где S — площадь поверхности грани ВС, т.е.

τ = F / S = Gg

где G — модуль сдвига.

Закон Гука для малой деформации сдвига выражается формулой:

Коэффициент G, зависящий от материала тела, называется модулем сдвига и характеризует упругие свойства тела при деформации сдвига. Например, для стального образца G = 76 ГПа.

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).

Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. Сдвиг при больших углах приводит к разрушению тела — срезу. Срез происходит при работе ножниц, пилы и др.

Обратите внимание на принципиальное отличие модуля кручения от модуля сдвига, который зависит только от материала. Модуль кручения зависит не только от материала, но ещё и от диаметра и от длины цилиндра

Деформации на примере организма человека

Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:

• Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
• Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
• Изгиб характерен для конечностей, костей таза, позвонков.
• Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.

Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.

По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.

Техническая механика



Сдвигом называют такой вид деформации, при которой в любом поперечном сечении бруса возникает только поперечная сила. Деформацию сдвига можно наблюдать, например, при резке ножницами металлических полос или прутков, при пробивании отверстия в заготовках на штампе (рис. 1).

Рассмотрим брус площадью поперечного сечения А, перпендикулярно оси которого приложены две равные и противоположно направленные силы F; линии действия этих сил параллельны и находятся на относительно небольшом расстоянии друг от друга. Для определения поперечной силы Q применим метод сечений (рис. 2). Во всех точках поперечного сечения действуют распределенные силы, равнодействующую которых определим из условия равновесия оставленной части бруса:

• Σ Y = 0 » F – Q = 0,
• откуда поперечная сила Q может быть определена, как:
• Q = F.

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении бруса при сдвиге. Очевидно, что при сдвиге в поперечном сечении возникают только касательные напряжения τ.

1. Предполагаем, что эти касательные напряжения равномерно распределены по сечению, и, следовательно, могут быть вычислены по формуле:
2. τ = Q / А.
3. На основании полученной формулы можно сделать вывод, что форма сечения на величину напряжения при деформации сдвига не влияет.
4. ***

Расчеты на прочность при сдвиге

Условие прочности детали конструкции заключается в том, что наибольшее напряжение, возникающее в ней (рабочее напряжение), не должно превышать допускаемое. Расчетная формула при сдвиге:

τ = Q / А ≤

читается следующим образом: касательное напряжение при сдвиге не должно превышать допускаемое. (при обозначении предельно допустимых напряжений применяют квадратные скобки: или ) По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку.

Деформация сдвига, доведенная до разрушения материала, называется срезом (применительно к металлам) или скалыванием (применительно к неметаллам). Допускаемое напряжение на срез выбирают для пластичных материалов в зависимости от предела текучести.

В машиностроении для штифтов, болтов, шпонок и других деталей, работающих на срез принимают = (0,25….0,35) σт, где σт – предел текучести материала изделия.

При расчетах на срез в случае, если соединение осуществляется несколькими одинаковыми деталями (болтами, заклепками и т. д.), полагают, что все они нагружены одинаково. Расчеты соединений на срез обычно сопровождают проверкой прочности этих соединений на смятие.

***



Для установления параметров, характеризующих деформацию при сдвиге, рассмотрим элемент бруса в виде параллелепипеда abcd, на грани которого действуют только касательные напряжения τ, а противоположную грань параллелепипеда представим жестко защемленной (рис. 3).

Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bc по отношению к сечению, принятому за неподвижное.

Деформация сдвига характеризуется углом γ (гамма) и называется углом сдвига, или относительным сдвигом. Величина bb1, на которую смещается подвижная грань относительно неподвижной, называется абсолютным сдвигом.

Относительный сдвиг γ выражается в радианах.

Напряжения и деформации при сдвиге связаны между собой зависимостью, которая называется закон Гука при сдвиге. Закон Гука при сдвиге справедлив лишь в определенных пределах нагрузок и формулируется так: касательное напряжение прямо пропорционально относительному сдвигу.

Математически закон Гука для деформации сдвига можно записать в виде равенства:

τ = G γ.

Коэффициент пропорциональности G характеризует жесткость материала, т. е. способность сопротивляться упругим деформациям при сдвиге, и называется модулем сдвига или модулем упругости второго рода.

Модуль упругости выражается в паскалях; для различных материалов его величина определена экспериментально и ее можно найти в специальных справочниках. При проведении ответственных расчетов на срез величина модуля упругости для каждого соединения определяется опытным путем, непосредственно перед расчетом, либо берется из справочника с применением увеличенного запаса прочности.

• Следует отметить, что между тремя упругими постоянными (модулями упругости) E, G и ν существует следующая зависимость:
• G = E / .
• Принимая для сталей ν ≈ 0,25, получаем: Gст ≈ 0,4 Ест .
• ***
• Материалы раздела «Сопротивление материалов»:



Заключение

Деформации, рассматриваемые в курсе школьной физики, оказывают влияние на процессы, происходящие в живом мире. В организмах человека, животных постоянно происходит кручение, изгиб, растяжение, сжатие. И для того чтобы осуществлять своевременную и полноценную профилактику проблем, связанных с осанкой или избыточным весом, медики используют зависимости, выявленные физиками при проведении фундаментальных исследований.

Например, прежде чем осуществлять протезирование нижних конечностей, выполняется детальный расчет максимальной нагрузки, на которую он должен быть рассчитан

Протезы подбираются для каждого человека индивидуально, так как важно учесть вес, рост и подвижность последнего. При нарушениях осанки применяют специальные коррекционные пояса, основанные на использовании деформации сдвига

Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций

Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций.